#4632. 隐蔽的居所

题目描述

在小G的家乡，有很多人住在一个大湖的边上。

他告诉小D，这个大湖可以被视作一个圆。一共有 $N$ 户人家， 他们住在这个圆的 $N$ 等分点上，每个 $N$ 等分点上恰好有一户人家.

这里的每户人家都有不同的信仰，其中第 $i$ 户人家信仰第 $i$ 种宗教。很显然，宗教对于生活会产生一定的影响，具体来说，相邻两户人家信仰的宗教的编号之差的绝对值不可以超过 $K$。

同时，有几户人家会不满其他的一些人，对于两户人家 $i$ 和 $j$，如果 $i$ 不喜欢 $j$ ，那么 $j$ 不可以住在 $i$ 顺时针方向的下一个位置上，这样的不满关系一共有 $M$ 对。

小D突然好奇起来了，这 $N$ 户人家一共有多少种不同的居住方法呢?

小D的方向感不好，所以如果两种方案可以通过顺时针旋转某个角度变成一样的，那么小D就不会认为这两种方案不同。

数据范围

对于所有数据,有 $1 \le N \le 10^6,0 \le M \le 10^5,0 \le K \le 3$

Subtask1 5%： $K = 0$

Subtask2 5%： $N = 1$

Subtask3 5%： $N = 2$

Subtask4 5%： $K = 1$

Subtask5 20%：$N \le 10$

Subtask6 20%：$K = 2$

Subtask7 20%：$M = 0$

Subtask8 20%：没有特殊的约定.

题解

 

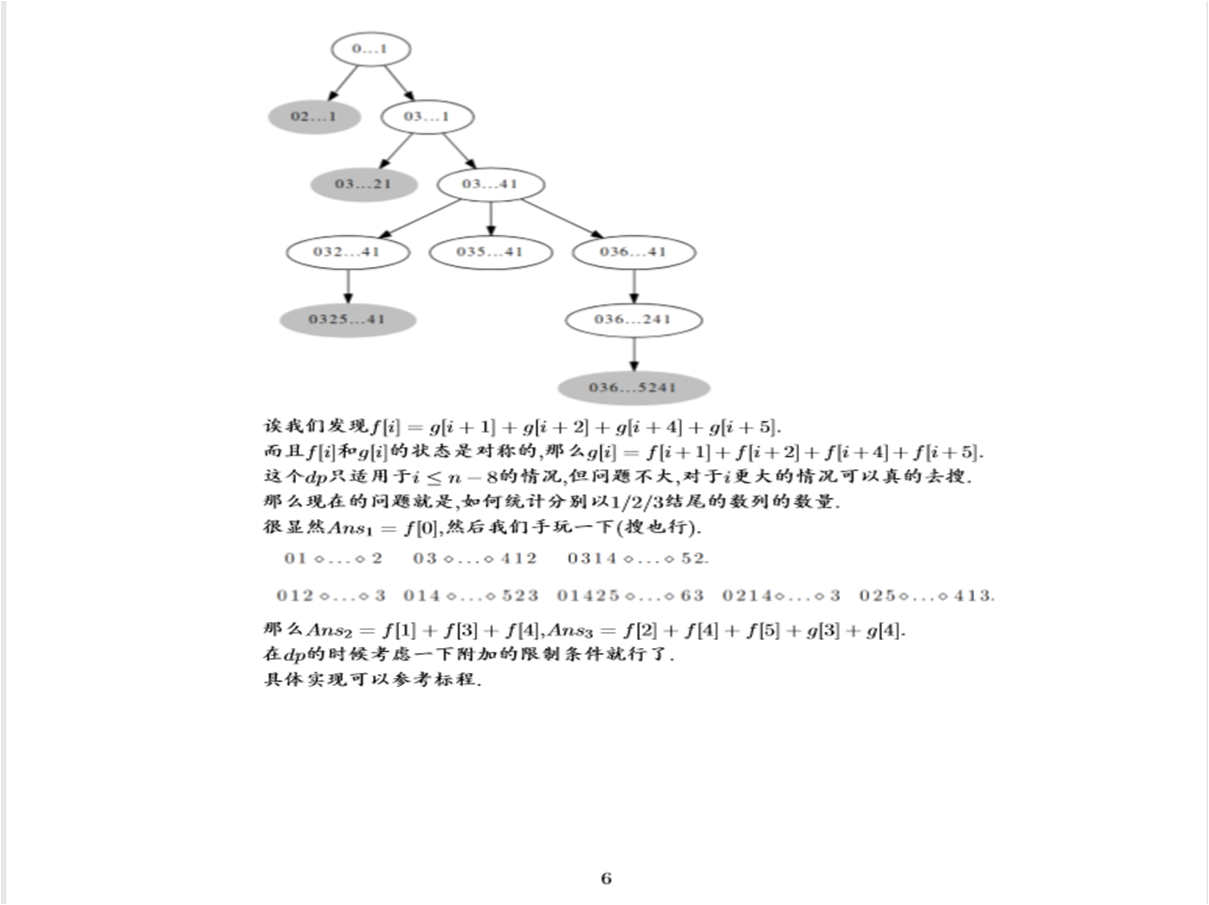
代码

 

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5,P=1e9+7; bool L[N][8];
int n,m,k,a[N],b[N],p[15],mp[15][15],ans,f[N],g[N],s1,s2,s3;
int A(int x){return x>0?x:-x;}
int X(int x){return x>=P?x-P:x;}
void W5(){
    for (int i=1;i<=n;i++) p[i]=i;
    for (int i=1;i<=m;i++) mp[a[i]][b[i]]=1;
    do{
        if (p[1]!=1) break;
        bool J=1;
        for (int i=1;i<n;i++)
            J&=(A(p[i]-p[i+1])<=k && !mp[p[i]][p[i+1]]);
        J&=(A(p[n]-p[1])<=k && !mp[p[n]][p[1]]);
        ans+=J;
    }while(next_permutation(p+1,p+n+1));
    printf("%d\n",ans);
}
void W6(){
    bool jx=0,ox=0;
    for (int i=1;i<=m;i++){
        if (A(a[i]-b[i])==1){
            if (a[i]!=1 && b[i]!=1) continue;
            if (a[i]==1) ox=1;else jx=1;
        }
        if (A(a[i]-b[i])==2){
            if (a[i]>b[i]){
                if (a[i]&1) ox=1;else jx=1;
            }
            else{
                if (a[i]&1) jx=1;else ox=1;
            }
        }
    }
    printf("%d\n",2-jx-ox);
}
bool vis[N];
void F(int u,int x,int l){
    if (x==n){
        if (A(l-u-1)<=3 && L[l][u+4-l]) f[u]++;
        if (f[u]>=P) f[u]-=P;return;
    }
    for (int i=-3;i<=3;i++)
        if (l+i>u+1 && l+i<n && !vis[l+i] && L[l][i+3])
            vis[l+i]=1,F(u,x+1,l+i),vis[l+i]=0;
}
void G(int u,int x,int l){
    if (x==n){
        if (A(l-u)<=3 && L[l][u-l+3]) g[u]++;
        if (g[u]>=P) g[u]-=P;return;
    }
    for (int i=-3;i<=3;i++)
        if (l+i>u+1 && l+i<n && !vis[l+i] && L[l][i+3])
            vis[l+i]=1,G(u,x+1,l+i),vis[l+i]=0;
}
int main(){
    scanf("%d%d%d",&n,&m,&k);
    for (int i=1;i<=m;i++)
        scanf("%d%d",&a[i],&b[i]);
    if (n<=10) return W5(),0;
    if (k==0) return puts("0"),0;
    if (k==1) return puts("0"),0;
    if (k==2) return W6(),0;
    for (int i=0;i<=n;i++)
        for (int j=0;j<=7;j++) L[i][j]=1;
    for (int i=1;i<=m;i++){
        a[i]=n-a[i];b[i]=n-b[i];
        if (A(a[i]-b[i])<=3)
            L[a[i]][b[i]-a[i]+3]=0;
    }
    f[n-2]=L[n-2][4];g[n-2]=L[n-1][2];
    for (int i=n-3;~i;i--){
        if (i>n-8) F(i,i+2,i),G(i,i+2,i+1);
        else{
            if (L[i][5]) f[i]=g[i+1];
            if (L[i][6] && L[i+2][2]) f[i]=X(f[i]+g[i+2]);
            if (L[i][6] && L[i+3][2] && L[i+2][6] && L[i+4][0]) f[i]=X(f[i]+g[i+4]);
            if (L[i][6] && L[i+3][6] && L[i+5][0] && L[i+2][5] && L[i+4][0]) f[i]=X(f[i]+g[i+5]);
            
            if (L[i+2][1]) g[i]=f[i+1];
            if (L[i+1][4] && L[i+3][0]) g[i]=X(g[i]+f[i+2]);
            if (L[i+1][6] && L[i+5][0] && L[i+2][4] && L[i+3][0]) g[i]=X(g[i]+f[i+4]);
            if (L[i+1][6] && L[i+4][1] && L[i+2][6] && L[i+6][0] && L[i+3][0]) g[i]=X(g[i]+f[i+5]);
        }
    }
    s1=f[0];
    
    if (L[0][4]) s2=f[1];
    if (L[0][6] && L[4][0] && L[1][4]) s2=X(s2+f[3]);
    if (L[0][6] && L[3][1] && L[1][6] && L[5][0]) s2=X(s2+f[4]);
    
    if (L[0][4] && L[1][4]) s3=f[2];
    if (L[0][4] && L[1][6] && L[5][0] && L[2][4]) s3=X(s3+f[4]);
    if (L[0][4] && L[1][6] && L[4][1] && L[2][6] && L[6][0]) s3=X(s3+f[5]);
    if (L[0][5] && L[2][2] && L[1][6]) s3=X(s3+g[3]);
    if (L[0][5] && L[2][6] && L[4][0] && L[1][5]) s3=X(s3+g[4]);
    
    if (L[1][2]) ans=s1;
    if (L[2][1]) ans=X(ans+s2);
    if (L[3][0]) ans=X(ans+s3);
    
    printf("%d\n",ans);return 0;
}