关于 JavaScript 的 精度丢失 与 近似舍入
一、背景
最近做 dashborad 图表时,涉及计算小数且四舍五入精确到 N 位。后发现 js 算出来的结果跟我预想的不一样,看来这里面并不简单……
二、JS 与 精度
1、精度处理
首先明确两点:
- 1、小数才会涉及精度的概念
- 2、小数的(存储和)运算涉及 JS 的
精度处理
在现实中,我们运算小数,不会出现任何问题。但是 JS (编程语言)里,却不是这样。
2、精度丢失
例如,在 JS 里执行:
0.1 + 0.2
0.30000000000000004
0.3 - 0.1
0.19999999999999998
0.1 * 0.1
0.010000000000000002
0.3 / 0.1
2.9999999999999996
可以看出,JS 运算小数的结果,并不是我们预想的那样。这就是精度丢失的问题。
(1)问:精度丢失会引发什么问题?
答:
- 1、让判断等于(
===)的逻辑出错。比如让0.1 + 0.2 === 0.3为false - 2、让本来可以预想到的结果精度变的特别大,小数点后位数特别长。比如若要前端显示,会特别难看。
(2)问:为什么会出现精度丢失?
答:这跟浮点数在计算机内部(用二进制存储)的表示方法有关。
JS 采用 IEEE 754 标准的 64 位双精度浮点数表示法,这个标准是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用,也被很多语言如 java、python 采用。
这个标准,会让大部分的十进制小数都不能用二进制浮点数来精确表示(比如转成二进制就会变成无限小数)。所以一般情况下,你输入的十进制小数仅由实际存储在计算机中的近似的二进制浮点数表示。
然而,许多语言在处理的时候,在一定误差范围内(通常极小)会将结果修正为正确的目标数字,而不是像 JS 一样将存在误差的真实结果转换成最接近的小数输出。
具体原理可以看《浮点数的二进制表示 —— 阮一峰》,这里不赘述了。
(3)问:怎么避免精度丢失?
方法一:中途变成整数来计算
比如我们要计算 0.1 + 0.2,就先把数字全部乘以 10 使之变成整数,再相加,最后把结果除以 10。
因为整数是不会出现精度丢失的问题。(况且整数根本就没有精度)
其实很多第三方的库,原理也是用的这个。
方法二:使用第三方库
- Math.js
- decimal.js
- big.js
- bignumber.js
方法三:使用 toFixed() 函数(推荐)
console.log(parseFloat((0.3 + 0.1).toFixed(1))) // 0.4
注意:toFixed() 最好跟 parseFloat() 搭配使用。因为 toFixed 返回的是字符串。
问:toFixed() 为什么要返回字符串,而不是小数?【重点】
答:因为 JavaScript 的数据类型,关于数字的只有 number 类型(不像 C 语言 or 数据库等还分 int、float、double),而对于 number 类型来说, 会忽略前置0和小数点后的后置0(比如 001 是 1; 1.1000 是 1.1)。
在下面还会继续介绍
toFixed()的关于舍入的特性。
三、JS 与 近似计算方法
在上面提到的:
- 精度计算
- 精度丢失
都会有可能让精度发生变化(即小数点后位数变化)。如果我们需要统一精度,那就需要用到近似(计算)方法。
1、四舍五入
(1)规则
四舍五入是最常见的近似计算方法,具体规则顾名思义,不赘述了。
(2)Math.round()
给定数字的值四舍五入到最接近的整数。
Math.Round(2.4) // 2
Math.Round(2.5) // 3
(3)_.round() —— lodash
给定数字的值四舍五入到最接近的数(可以是小数)。
lodash 的这个方法,我看了源码,底层也是调用的 Math.round(),只是加了一些额外功能,比如第二个参数,可以指定四舍五入的精度。
const _ = require('lodash');
_.round(1.04, 1) //1
_.round(1.05, 1) //1.1
(4)四舍五入真的公平吗?【重点】
因为自己很小的时候就在学校学到了四舍五入,一直想当然的认为四舍五入是公平的,等到现在细想的时候,才发现,真的不公平。
例如,想象一个场景,你的余额宝,每天会自动结算利息,但是可能(按照利息规则)算出来的值的小数有很多位,假设支付宝只支持到角,那么支付宝系统帮你记账的时候,肯定会给你近似计算,如果他用的是四舍五入的方法:
const _ = require('lodash');
console.log(_.round(1.01, 1)) //1 (我亏了0.01)
console.log(_.round(1.02, 1)) //1 (我亏了0.02)
console.log(_.round(1.03, 1)) //1 (我亏了0.03)
console.log(_.round(1.04, 1)) //1 (我亏了0.04)
console.log(_.round(1.05, 1)) //1.1 (我赚了了0.05)
console.log(_.round(1.06, 1)) //1.1 (我赚了0.04)
console.log(_.round(1.07, 1)) //1.1 (我赚了0.03)
console.log(_.round(1.08, 1)) //1.1 (我赚了0.02)
console.log(_.round(1.09, 1)) //1.1 (我赚了0.01)
首先,1 块钱整和 2 块钱整可以不用考虑,其次,如果假设 1.01 到 1.09 这 9 个数出现的概率一致。那么最后支付宝肯定要亏本,因为 1.05 划分到 1.1 是不公平的。
也可以画一个数轴来体现:
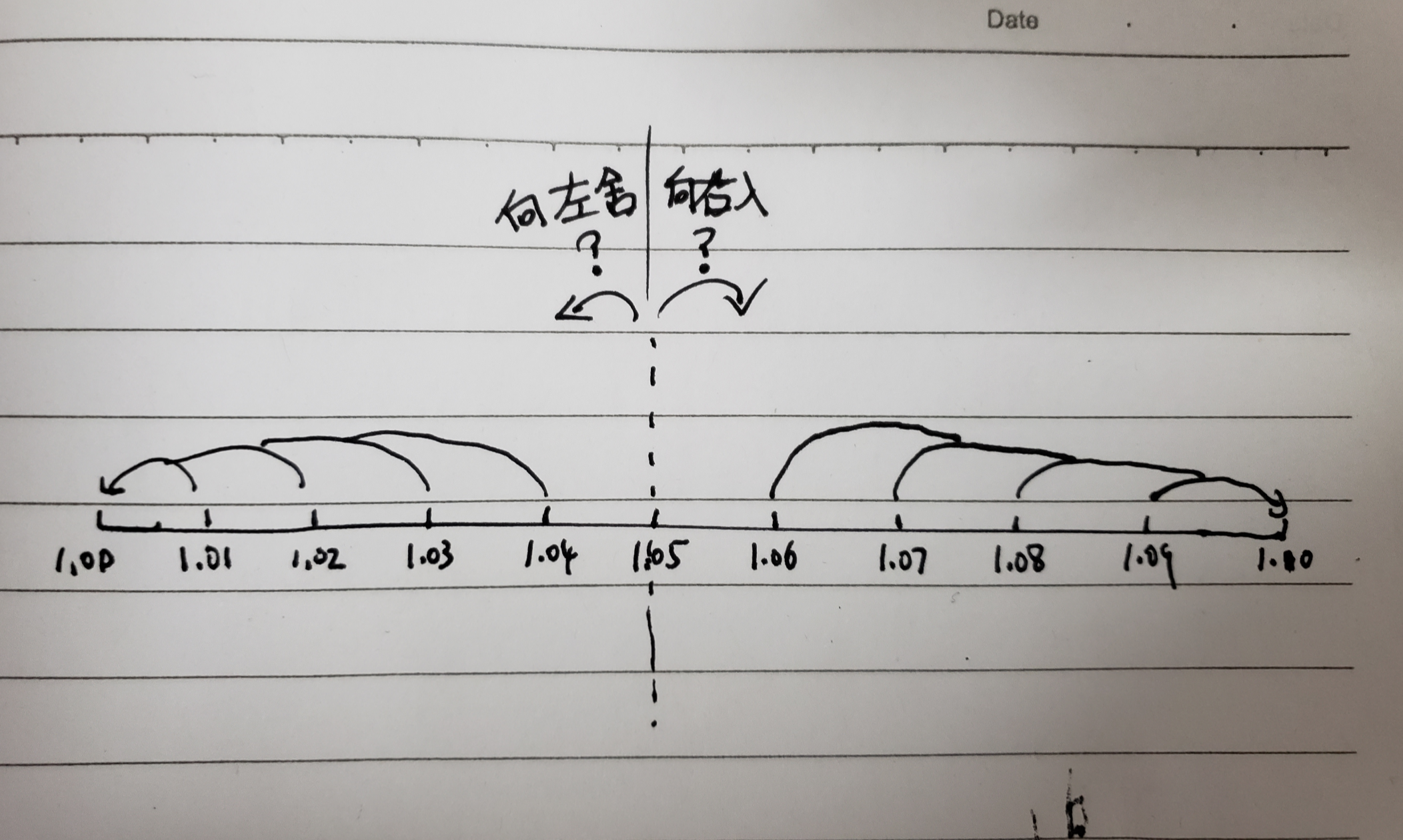
那么如何做到更公平的近似计算呢?可以用下面介绍的银行家舍入。
2、银行家舍入
国际通行的是 银行家舍入(Banker's rounding)算法 。
是 IEEE 规定的舍入标准。因此所有符合 IEEE 标准的语言都应该是采用这一规则的。
(1)规则
银行家舍入又称四舍六入五取偶(又称四舍六入五留双)法。
所以规则就是:四舍六入五考虑,五后非空就进一,五后为空看奇偶,五前为偶应舍去,五前为奇要进一。
关键就是“五后为空看奇偶”,因为如果是舍入位是5,无论是舍还是入都不公平,那就交给它前一位的奇偶性来判断,因为奇偶性分布概率是公平的。
当然只能说银行家舍入算法比四舍五入算法更科学,而不能说它就是绝对正确,而四舍五入就是错误的,因为这些结果都是基于统计数据产生的,前提就是这些数据摇符合随机性分布的要求。
(2)使用
目前 JS 上原生不支持,如果想使用:
- 1、自己实现
- 2、使用第三方 npm 包,如 bankers-rounding
3、toFixed
toFixed() 部分符合银行家舍入的规则。
(1)四舍六入
符合
(2)五后非空就进一
符合
(3)五后为空看奇偶,五前为偶应舍去,五前为奇要进一
部分符合
// //toFixed结果 //银行家舍入结果
console.log(1.05.toFixed(1)) //1.1(+0.05) 1.0(-0.05)
console.log(1.15.toFixed(1)) //1.1(-0.05) 1.2(+0.05)
console.log(1.25.toFixed(1)) //1.3(+0.05) 1.2(-0.05)
console.log(1.35.toFixed(1)) //1.4(+0.05) 1.4(+0.05)
console.log(1.45.toFixed(1)) //1.4(-0.05) 1.4(-0.05)
console.log(1.55.toFixed(1)) //1.6(+0.05) 1.6(+0.05)
console.log(1.65.toFixed(1)) //1.6(-0.05) 1.6(-0.05)
console.log(1.75.toFixed(1)) //1.8(+0.05) 1.8(+0.05)
console.log(1.85.toFixed(1)) //1.9(+0.05) 1.8(-0.05)
console.log(1.95.toFixed(1)) //1.9(-0.05) 2.0(+0.05)
// //总计(+0.1) //总计(0)
可以看出 toFixed 肯定是不遵守四舍五入的,但是也跟银行家舍入算法有出入。(具体为什么是这样的计算方法,鄙人并不是弄清楚,待写)
4、其他 近似计算 函数
- Math.ceil():向上舍入(取整)
- Math.floor():向下舍入(取整)
- 等等……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号