Transformer
一、Vanilla Transformer（Post-LN Transformer）
1. model architecture
Transformer的结构也是一个encoder-decoder结构，其中，encoder和decoder是使用self-attention和全连接层堆叠的结构，如图1所示。
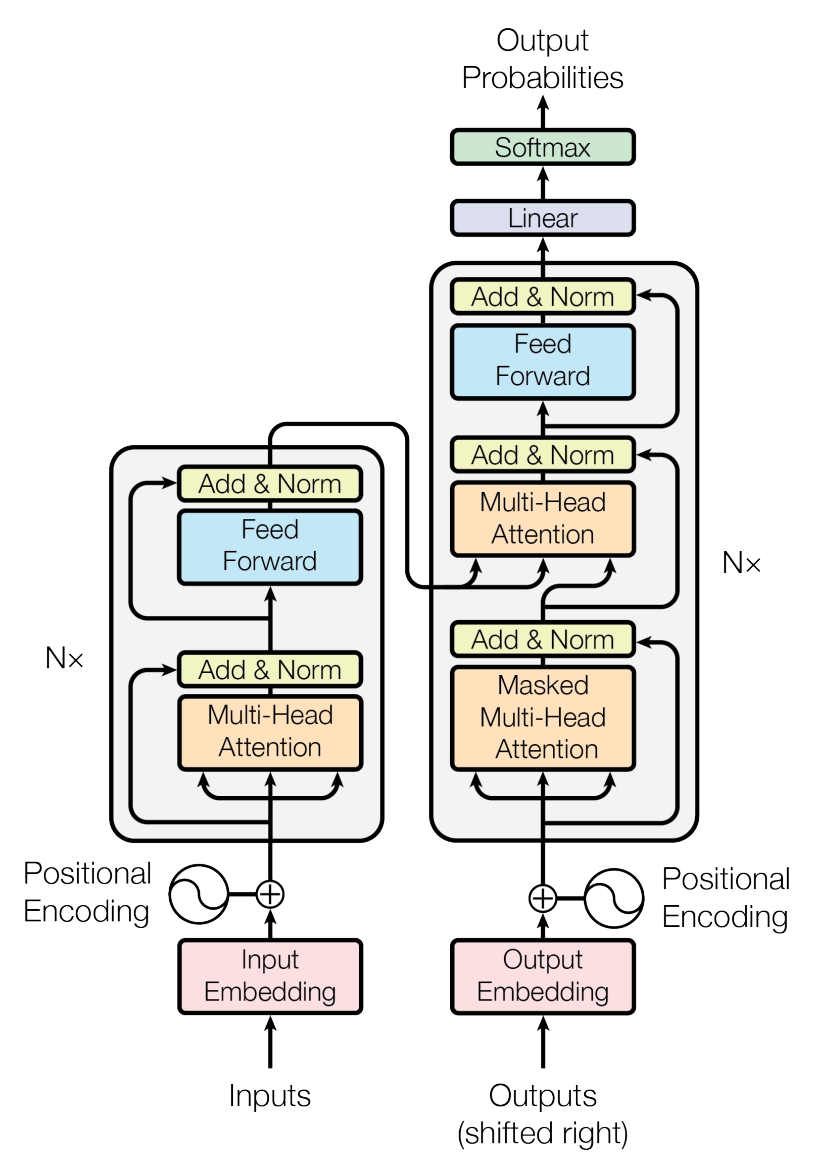
图1 Transformer结构
1.1 Eocoder和Decoder
1.1.1 Encoder
Encoder由N个相同的层堆叠成，每个层由两部分组成：多头注意力机制（multi-head self-attention mechanism）和全连接层（fully connected feed-forward network）。
在每部分之间加上了残差连接（residual connections）和LayerNorm。
1.1.2 Decoder
Decoder也是由N个相同的层堆叠成，除了像Encoder的两个部分之外，还插入了带三个部分，该部分对Encoder的输出执行多头注意力。同时，和Encoder一样，每个部分
也都加上残差连接和LayerNorm。在Decoder中的自注意力（self-attention）部分，为了防止防止当前位置看到后续位置，引入了mask，使得第$i$个位置的预测值只依赖于位置$i$前面的位置信息。
1.2 Attention
Attention可以理解为query和key-value集合到输出的一个映射。其中，query、keys、values和输出都是向量。输出通过value值的加权和得到。权重通过key、value计算得到。
1.2.1 Scaled Dot-Product Attention
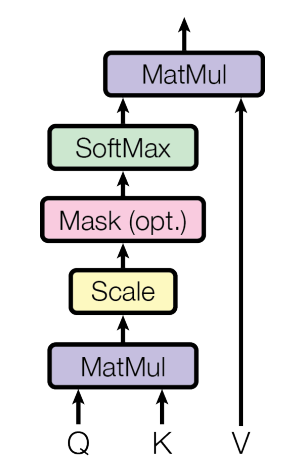
图2 Scaled Dot-Product Attention
Scaled Dot-Product Attention其实就是一个单头注意力机制，通过缩放的点乘实现，如图2所示。输入由维度为$d_{k}$的queries和keys以及维度为$d_{v}$的values组成。通过计算queries点乘keys，
然后除以$\sqrt{d}$，再经过softmax函数获得权重weights。最后由权重和values做加权求和得到attention的值。实际操作过程中，使用如下的矩阵运算求得。
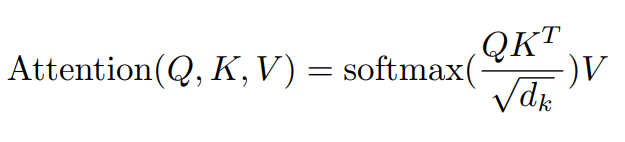
为什么要除以 $\sqrt{d}$？
1. 因为随着$d_{k}$得变大，Q和K点乘得值很大，使得经过softmax之后梯度消失。因此除需要以$d_{k}$。
2. 使得点乘得值和原先分布一致：假设$Q$和$K$中得元素都是相互独立的、均值为0、方差为1的随机变量，点乘之后得值服从均值为0，方差为$d_{k}$。
为了使得点乘得值符合均值为0，方差为1，所以需要除以$\sqrt{d}$。
1.2.2 Multi-Head Attention
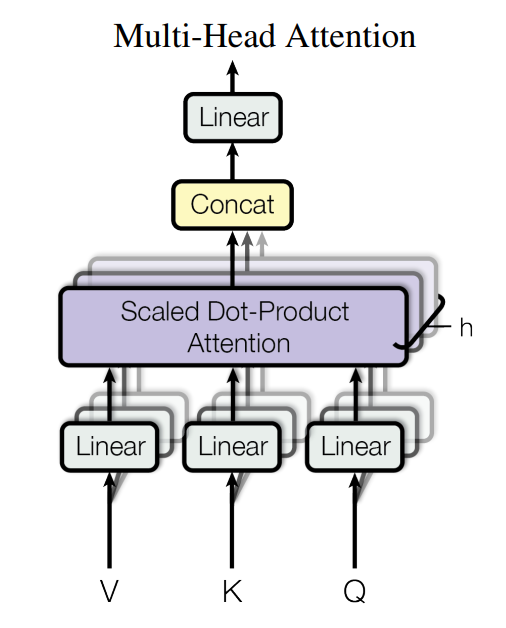
图3 Multi-Head Attention
多头注意力机制如图3所示，具体操作如下，通过Linear层将queries、keys和values投射成$h$个$d_{q}$、$d_{k}$、$d_{v}$。执行attention之后将结果concat起来，得到最终的values。
多头注意力允许模型在不同位置联合处理来自不同表示子空间的信息。多头注意力机制可由如下矩阵运算得到。
1.2.3 Transformer中的Attention
Transformer中以三种不同的方式使用多头注意力机制。
1. encoder-decoder attention，queries来自前面的decoder层，而keys和values来自encoder的输出。
2. encoder包含的self-attention。
3. decoder中的self-attention。为了防止decoder中的向左的信息流，我们通过将需要mask的值设置成非常小的值，比如-1e-10。这样经过softmax之后，接近于0。
1.3 Position-wise Feed-Forward Networks
其实就是全连接层（也可以是1*1卷积），中间有ReLU，如下所示。
1. 4 Positional Encoding
这里使用的Positional Encoding如下：
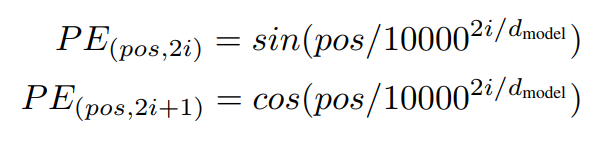
可以通过如下代码画出Positional Encoding。
1 def get_positional_encoding(seq_len, seq_dim): 2 pe = np.zeros((seq_len, seq_dim)) 3 4 pos = np.arange(seq_len)[:, None] 5 div_term = np.exp(-np.arange(0, seq_dim, 2) / seq_dim * math.log(10000)) 6 pe[:, 0::2] = np.sin(pos * div_term) 7 pe[:, 1::2] = np.cos(pos * div_term) 8 return pe 9 10 11 img = get_positional_encoding(100, 256) 12 cax = plt.matshow(img) 13 plt.gcf().colorbar(cax) 14 plt.savefig("positional_encoding.jpg") 15 plt.show()
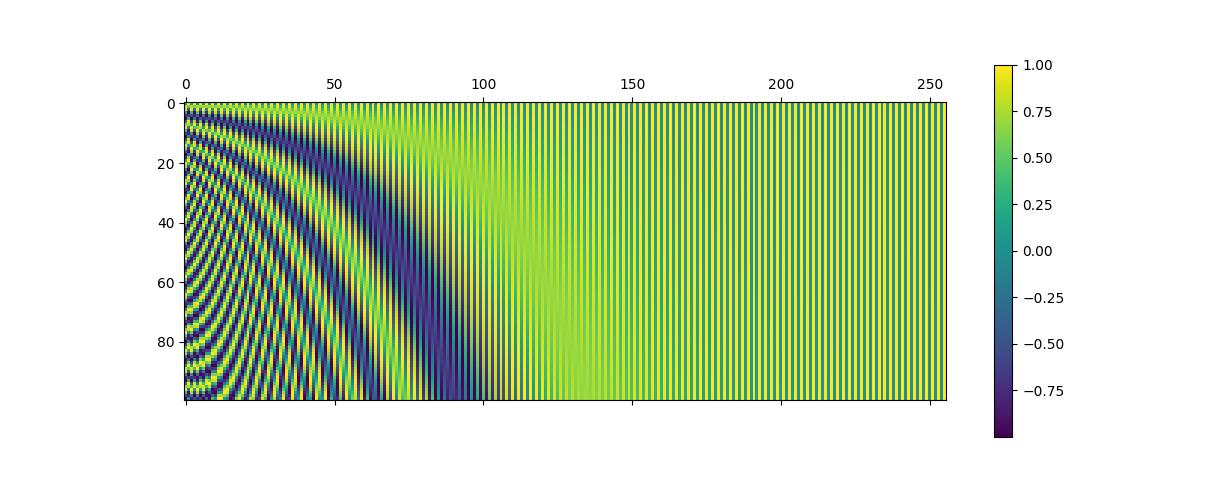
图4 Positional Encoding
2. 训练
Vinilla Transformer使用warmup策略调整学习率，其公式如下：
$lr=d_{model}^{-0.5}\cdot min(step^{-0.5}, step \cdot warmup^{-1.5})$
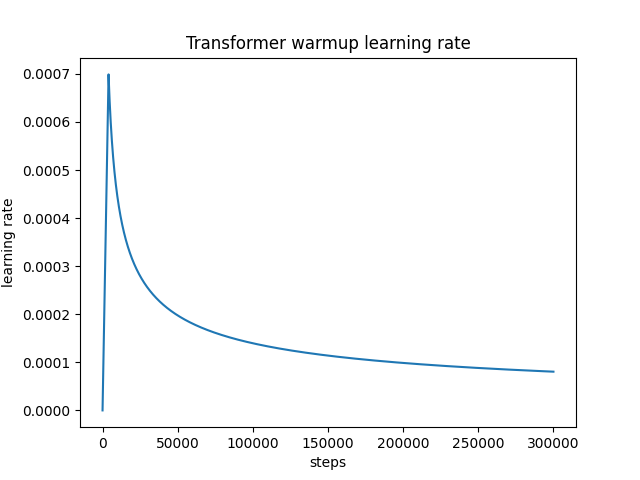
图5 Learning Rate
二、Pre-LN Transformer
因为再上面的Post-LN Transformer中，warmup学习率调整时关键的。但是这样的warmup不仅减慢了模型的优化过程，而且带来了更多的超参数调整。
模型的最终精度对最大的学习率和warmup的迭代次数非常敏感。因此调整如此敏感的超参数在训练大规模模型时成本很高。
我们使用平均场论来研究在初始化阶段的优化行为。根据我们的理论分析，当将layer normalization放置在残差块中间（即Post-LN Transformer）时，
在输出层附近的参数的梯度很大，因此如果没有warmup而直使用一个大的学习率会使得优化过程很不稳定。使用warmup，并以较小的学习率训练模型避免了这个问题。
而对于Pre-LN Transformer，无论是理论上还是经验上，梯度都表现良好，没有任何爆炸或消失，因此可以不使用warmup。
