生成式AI之Flow-Based Model

1、数学基础

1.1 雅可比矩阵Jacobian

雅可比矩阵是一阶偏导数以一定方式排列成的矩阵。

假设：

$z=\begin{bmatrix}z_{1}\\z_{2}\end{bmatrix}$, $x=\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}$

$x=f(z)$

则，jacobian如下：

$J_{f}=\begin{bmatrix}\partial x_{1}/\partial z_{1} &\partial x_{1}/\partial z_{2} \\\partial x_{2}/\partial z_{1} &\partial x_{2}/\partial z_{2}\end{bmatrix}$

如果逆函数$f^{-1}$符合如下条件：

$z = f^{-1}(x)$，则$f^{-1}$函数的jacobian为：

$J_{f^{-1}}=\begin{bmatrix}\partial z_{1}/\partial x_{1} &\partial z_{1}/\partial x_{2} \\\partial z_{2}/\partial x_{1} &\partial z_{2}/\partial x_{2}\end{bmatrix}$

 其中，$J_{f}J_{f^{-1}}=I$

1.2 行列式Determinant

行列式的含义：

如下图所示，在高维空间中，行列式的绝对值代表了高维空间的体积，如果是2*2 matrix，就是一个面积。

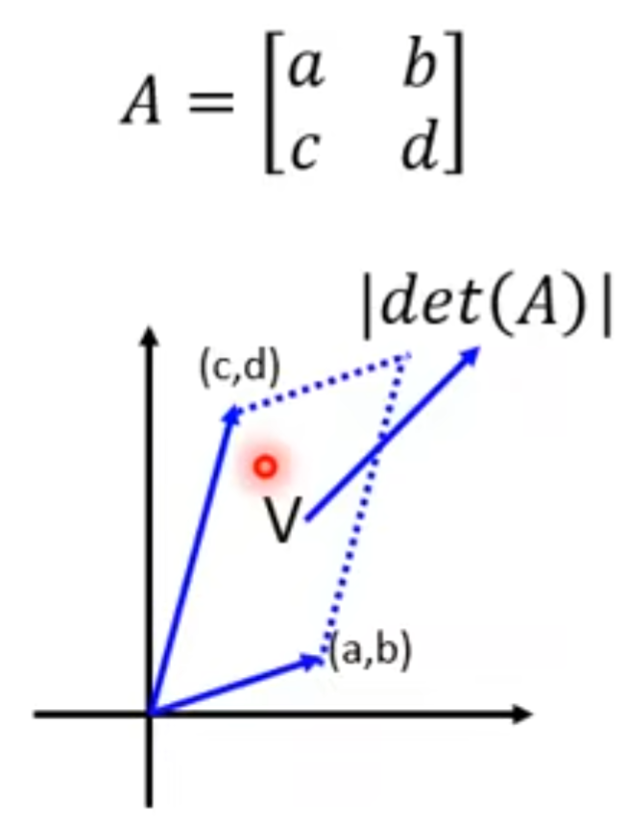
 行列式有如下的关系：

$det(A)=\frac{1}{det(A^{-1})} $，因此jacobian关系如下：

$p({x}')\left |det(J_{f})\right|=\pi({z}')$

$det(J_{f})=\frac{1}{det(J_{f^{-1}})} $

 

1.3 Change of variable theory

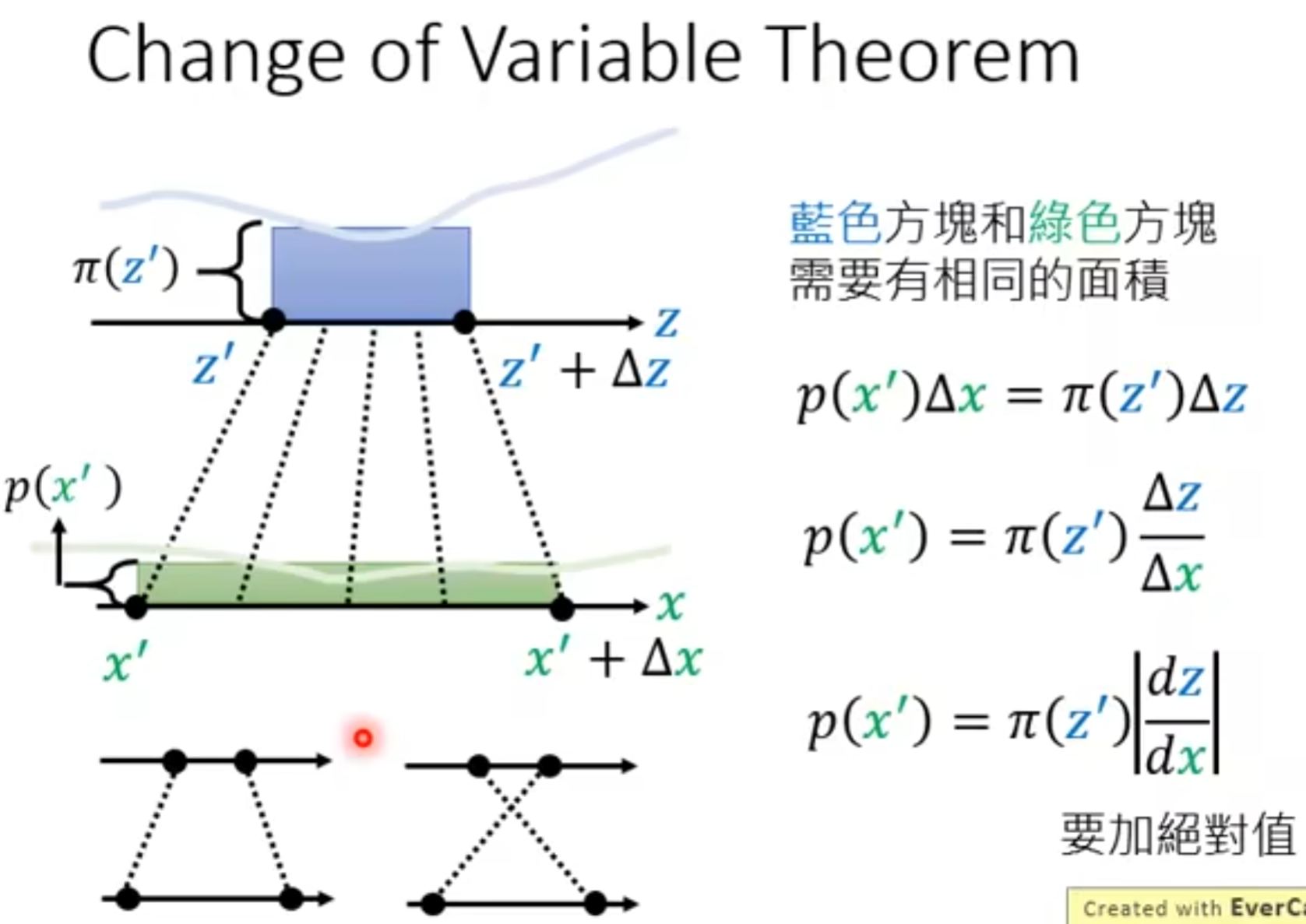
 最终有如下关系：

$p({x}')=\pi({z}')\left |det(J_{f^{-1}})\right|$

 

2. flow-based model原理

 对于生成器G，其定义了一个概率分布$P_{G}$，如下图所示：

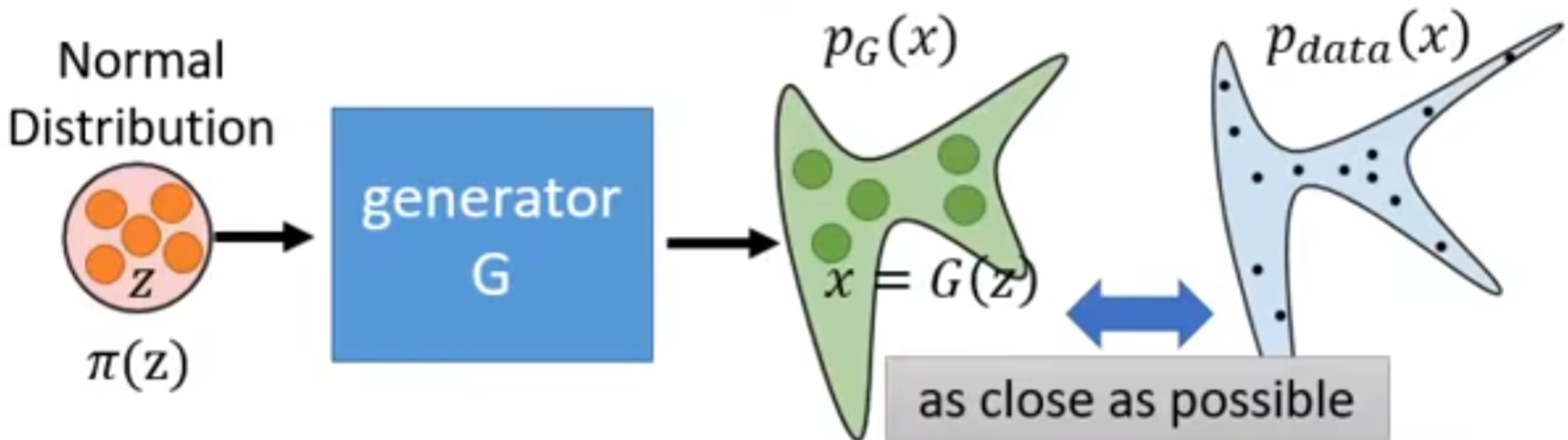
我们的目标就是使得在真实数据中采样得到的数据在$P_{G}$最大，即最大似然：

$G^{*}=argmax\sum_{i=1}^{m}logP_{G}(x^{i}) $，其中，$x^{i}$来自$P_{data}$。

flow-based model可以直接最优化上述objective function。

 

$p_{G}(x^{i})=\pi (z^{i})\left | det(J_{G^{-1}})\right| $，因为$z^{i}=G^{-1}(x^{i})$，因此：

$logp_{G}(x^{i})=log\pi(G^{-1}(x^{i}))+log\left |det(J_{G^{-1}}) \right| $

 需要求解上述$logp_{G}$，需要好好设计网络，使得其能够计算行列式$det(J_{G})$以及需要能够直到$G^{-1}$。

这里为了确保$G$是可逆的，所以这里输入$z$和输出$x$的维度是一样的。而VAE、GAN可以是不一样维度的。

 

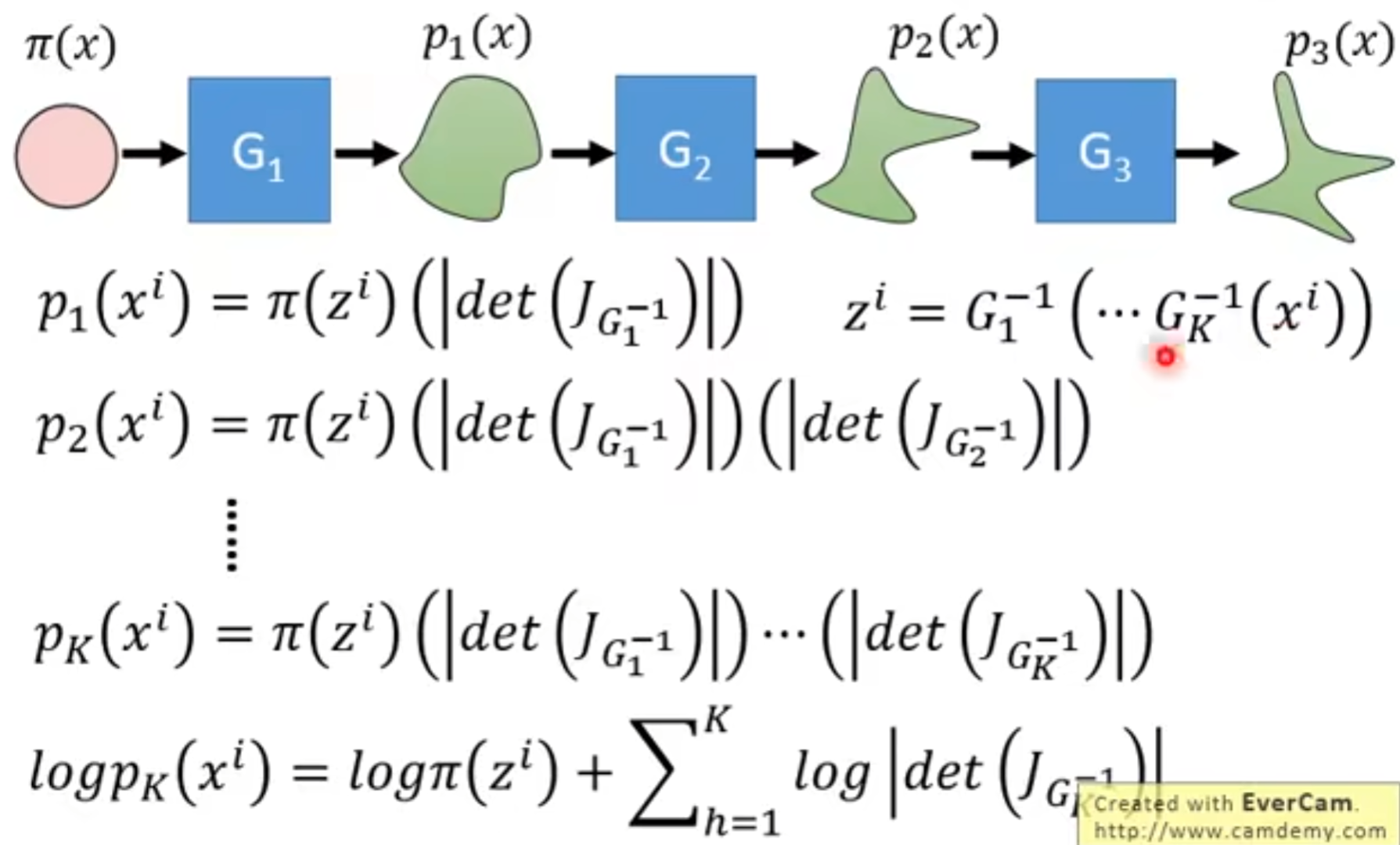
 看上面公式，我们在训练的时候实际上训练的是$G^{-1}$，在生成的时候将$G^{-1}$倒过来得到$G$。

 

1. 可逆网络

为了使得network $G$是可逆的，这里使用coupling layer：

 

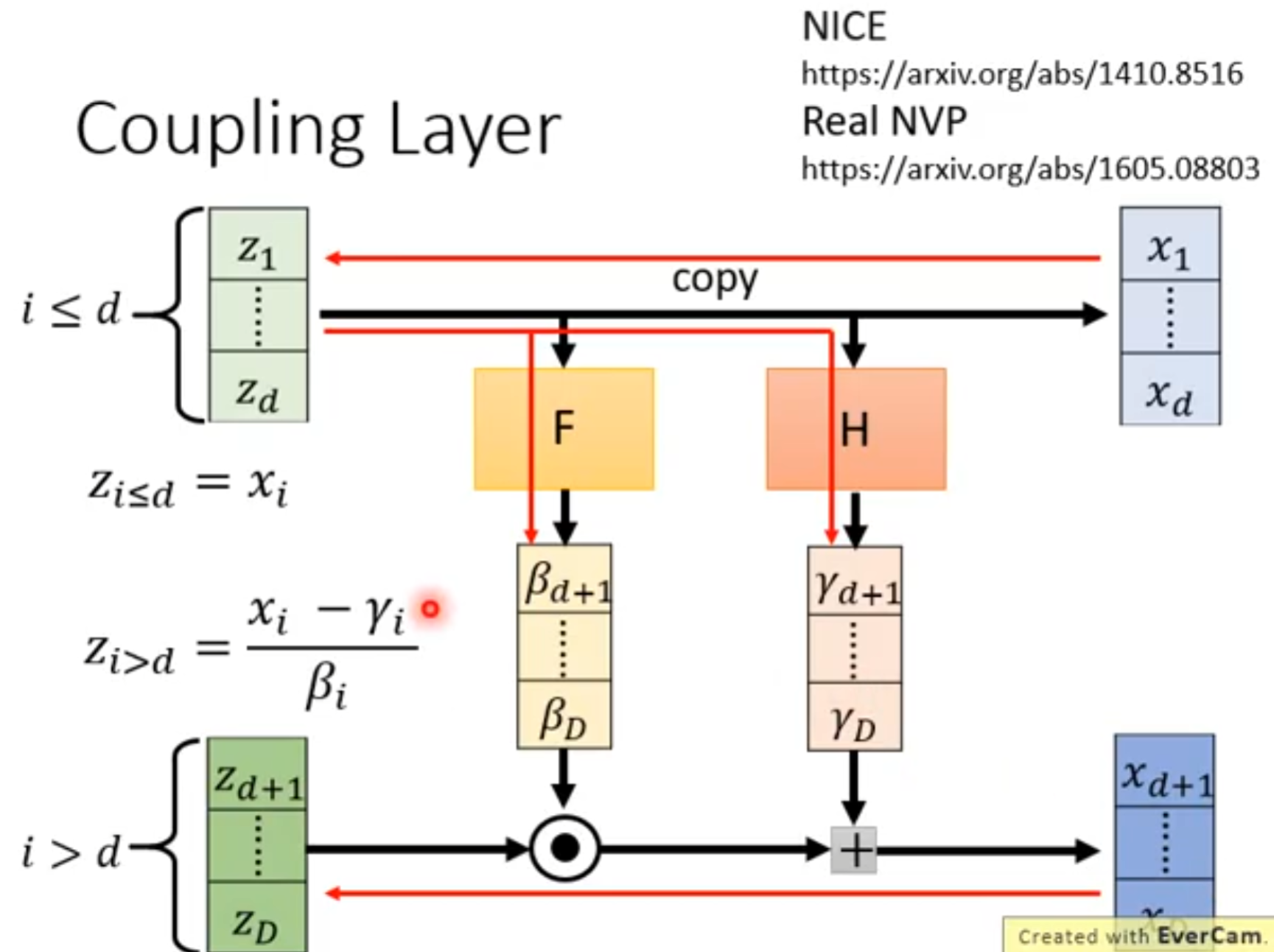
2. 可以计算行列式determinant

这里的determinant等于右下角的determinant。

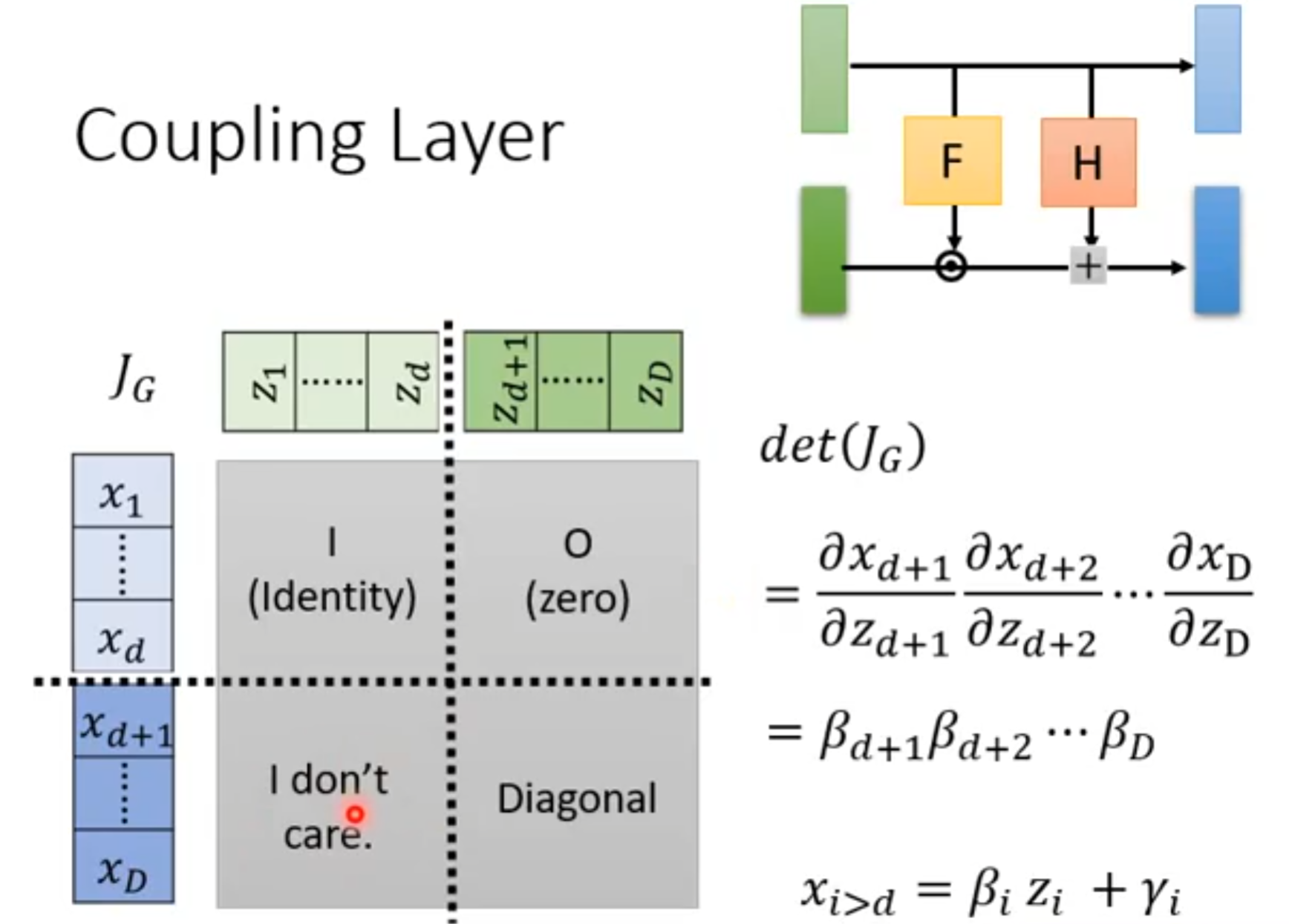
 这里jacobian $J_{G}$的determinant $det(J_{G})$就是函数F的输出的元素相乘。