生成式AI之DDPM
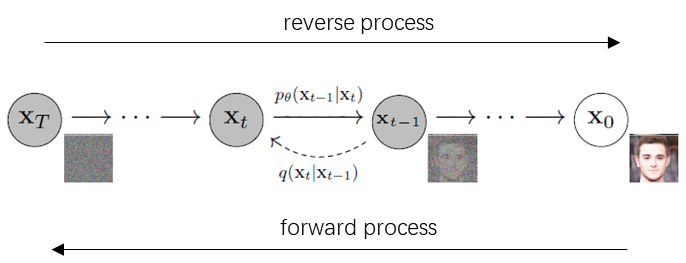
扩散过程是一个逐渐在数据上加噪的马尔科夫链,直到最终变成一个完全的噪声。而扩散模型就是一个使用变分推断训练的参数化马尔科夫链。如上图所示。学习的是一个reverse process。
前提条件:
1. 马尔可夫性质:当前的状态只与之前一个时刻的状态有关;
2. 前向和反向状态服从高斯分布,而且变化比较小(利于数学分析);
扩散模型的前向过程就是不断在数据上加噪的过程,可以使用如下形式表示,其中:
$q(x_{1:T}|x_{0}):=\prod_{t=1}^{T}q(x_{t}|x_{t-1})$ $q(x_{t}|x_{t-1}) :=\mathcal{N}(x_{t};\sqrt{1-\beta_{t}}x_{t-1},\beta_{t}I)$
这里为了后续计算方便,将条件概率的均值和方差设置成$\sqrt{1-\beta_{t}}x_{t-1}$和$\beta_{t}$。其中,$0<\beta_{1}<\beta_{2}<...<\beta_{t-1}<\beta_{t}<1$。
扩散模型的反向过程,可以使用如下的概率形式表示,将其定义为可学习的马尔科夫链,该过程的起始点为$p({x}_{T})=\mathcal{N}({x}_{T};0,I)$。
$p_{\theta}(x_{0:T}):=p(x_{T})\prod_{t=1}^{T}p_{\theta }(x_{t-1}|x_{t})$ $p_{\theta }(x_{t-1}|x_{t}):=\mathcal{N}(x_{t-1};\mu_{\theta}(x_{t}, t), {\textstyle \sum_{\theta}(x_{t},t)})$
所以扩散模型就是通过学习,来估计$;\mu_{\theta}(x_{t}, t)$和${\textstyle \sum_{\theta}(x_{t},t)})$的过程。
DDPM的前向加噪过程如下:
每次加噪过程如下:
$q(x_{t}|x_{t-1})=\mathcal{N}(x_{t};\sqrt{1-\beta_{t}}*x_{t-1},\beta_{t}I)$
$x_{t}=\sqrt{1-_{\beta_{t}}}*x_{t-1}+\sqrt{\beta_{t}}*\varepsilon_{t-1}$ $0<\beta_{1}<\beta_{2}<...<\beta_{t-1}<\beta_{t}<1$。
引入新变量$\alpha_{t}=1-\beta_{t}$
因此上面加噪的过程可以写成:
$x_{t}=\sqrt{\alpha_{t}}*x_{t-1} + \sqrt{1-\alpha_{t}}*\varepsilon_{t-1}$
$x_{t-1}=\sqrt{\alpha_{t-1}}*x_{t-2} + \sqrt{1-\alpha_{t-1}}*\varepsilon_{t-2}$
合并上面两式,得:
$x_{t}=\sqrt{\alpha_{t}\alpha_{t-1}}*x_{t-2}+\sqrt{\alpha_{t}(1-\alpha_{t-1})}*\varepsilon_{t-2}+\sqrt{1-\alpha_{t}}*\varepsilon_{t-1} $
$x_{t}=\sqrt{\alpha_{t}\alpha_{t-1}}*x_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}*\varepsilon_{t}$
以此类推,得到:
$x_{t}=\sqrt{\alpha_{t}\alpha_{t-1}...\alpha_{2}\alpha_{1}}*x_{0}+\sqrt{1-\alpha_{t}\alpha_{t-1}...\alpha_{2}\alpha_{1}}*\varepsilon_{t} =\sqrt{\bar{\alpha_{t}}}*x_{0}+\sqrt{1-\bar{\alpha_{t}}}*\varepsilon_{t} $
其中,$\bar{\alpha_{t}}=\alpha_{t}\alpha_{t-1}...\alpha_{2}\alpha_{1}$
因此,实际的前向过程中,$t$时刻的图片是直接使用上面的关系一次加噪完成的。
重采样
一个高斯分布不可导,可以将其转换成标准高斯分布的格式:
$y=\sigma*\varepsilon+\mu \sim \mathcal{N}(\mu,\sigma^{2}) $
所以,这里$x_{t}$满足高斯分布,且
$x_{t} \sim \mathcal{N}(\sqrt{1-\beta_{t}}*x_{t-1},\beta_{t})$
DDPM的反向生成过程如下:
由上描述的扩散过程$p(x_{T})p_{\theta}(x_{T-1}|x_{T})...p_{\theta}(x_{t-1}|x_{t})...p_{\theta}(x_{0}|x_{1}$)
其中,定义$p_{\theta}(x_{t-1}|x_{t})$为高斯过程,即:
$p_{\theta }(x_{t-1}|x_{t}):=\mathcal{N}(x_{t-1};\mu_{\theta}(x_{t}, t), {\textstyle \sum_{\theta}(x_{t},t)})$
实际上,在训练的时候,反向过程的$x_{0}$已知,因此反向过程也是一个确定的过程。
贝叶斯公式$q(x_{t-1}|x_{t})=\frac{q(x_{t}|x_{t-1})q(x_{t-1})}{q(x_{t})}$。
在推理的时候$q(x_{t-1})$,$q(x_{t})$未知,但是在训练的时候,$q(x_{t-1}|x_{0})$,$q(x_{t}|x_{0})$已知,因此:
$q(x_{t-1}|x_{t},x_{0})=\frac{q(x_{t}|x_{t-1},x_{0})q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$
因为每个分布都是高斯分布,即:
$q(x_{t}|x_{t-1})=\mathcal{N}(x_{t};\sqrt{1-\beta_{t}}*x_{t-1},\beta_{t}I)$
$q(x_{t}|x_{0})=\mathcal{N}(x_{t};\sqrt{\bar{\alpha_{t}}}*x_{0},(1-\bar{\alpha_{t}})I)$
$q(x_{t-1}|x_{0})=\mathcal{N}(x_{t-1};\sqrt{\bar{\alpha_{t-1}}}*x_{0},(1-\bar{\alpha_{t-1}})I)$
推理得到:
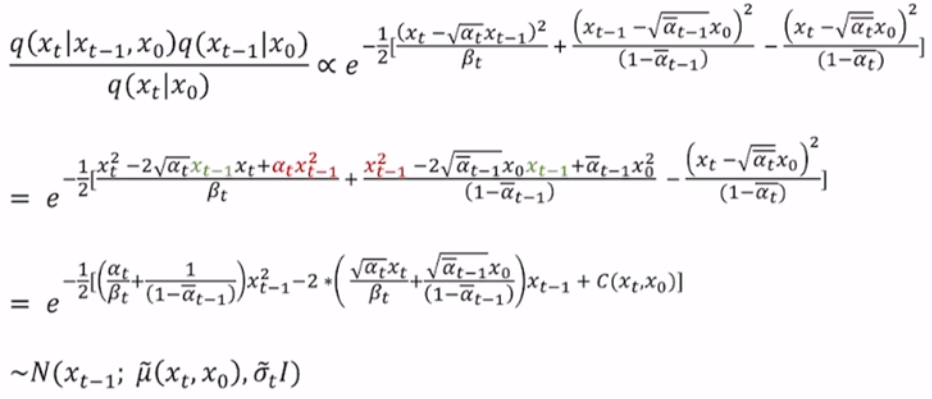

因此DDPM的前向和反向过程如下:
前向扩散:$q(x_{t}|x_{t-1})=\mathcal{N}(x_{t};\sqrt{1-\beta_{t}}*x_{t-1},\beta_{t}I)$
反向生成:$q(x_{t-1}|x_{t},x_{0})=\mathcal{N}(x_{t};\frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{1-\alpha_{t}}{\sqrt[]{1-\bar{\alpha_{t}}}}\varepsilon_{t}),\beta _{t}*\frac{1-\bar{\alpha _{t-1}}}{1-\bar{\alpha _{t}}}I)$
这里只需要通过模型预测$\varepsilon_{t}$即可。
这里预测的高斯噪声$\varepsilon_{t} $只是均值$\mu$里面的一部分,所以在生成的时候,还需要加噪一个额外的高斯噪声, 这样才能使得$q(x_{t-1}|x_{t})$符合高斯噪声。
DDPM训练优化目标
和所有的生成式模型一样,DDPM就是求模型的最大对数似然。
因为扩散过程的如下:
$P_{\theta}(x_{0})=\int_{x_{1}:x_{T}}p(x_{T})p_{\theta}(x_{T-1}|x_{T})...p_{\theta}(x_{t-1}|x_{t})...p_{\theta}(x_{0}|x_{1})dx_{1}:x_{T}$
因此,由Jensen不等式$f(E[X])\ge E[f(X)]$,可得:
$logP_{\theta}(x_{0})=log\int p_{\theta}(x_{0:T})dx_{1:T}=log\int \frac{p_{\theta(x_{0:T})}q(x_{1:T}|x_{0})}{q(x_{1:T}|x_{0})}dx_{1:T}\ge \int q(x_{1:T}|x_{0})log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_{0})}dx_{1:T}=E_{q(x_{1:T}|x_{0})}[log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_{0})}]=E_{q(x_{1:T}|x_{0})}[logp(x_{T})+\sum_{t\ge1}log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t}|x_{t-1})}]$
因此扩散模型就是最大化$logP_{\theta}(x_{0})$,即损失函数为最小化负对数似然,即:
$E_{q(x_{1:T}|x_{0})}[-log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_{0})}]$
经过如下推导:
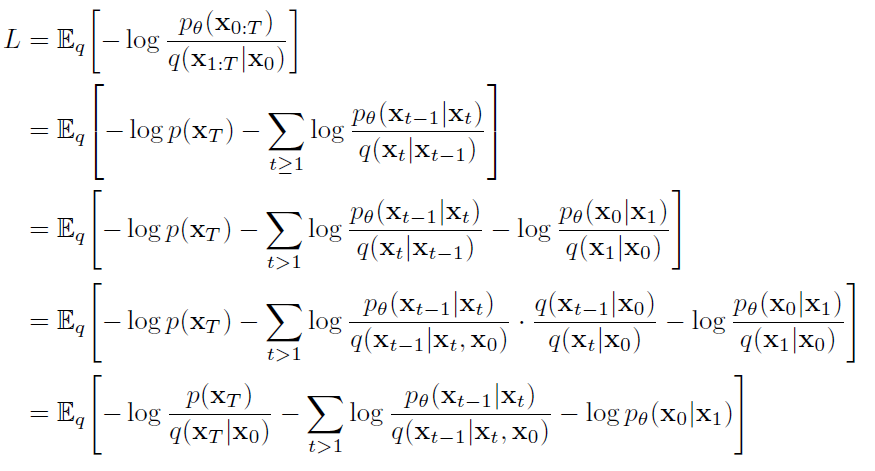
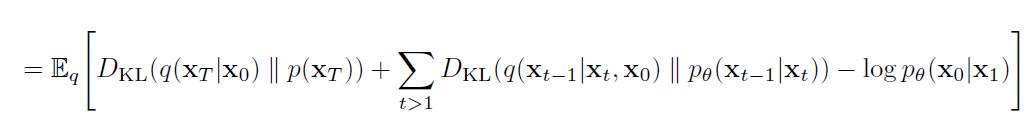
其中的三个分量分别为$L_{T}$,$L_{t-1}$,L_{0},如下所示。
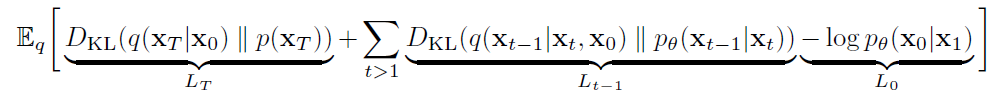
对于$L_{T}$而言,其含义为前向加噪的终点和模型推理的时候的起点高斯噪声尽可能接近。即$x_{t}=\sqrt{\bar{\alpha_{t}}}*x_{0}+\sqrt{1-\bar{\alpha_{t}}}*\varepsilon$和$\varepsilon$尽可能接近。因为在超参数设置的时候,$\bar{\alpha_{t}}$在t=T时趋近于0。因此不需要考虑$L_{T}$。
对于$L_{0}$而言,其含义为$x_{1}$和$x_{0}$尽可能接近,这一项也可以通过设置超参数实现,因此这一项也不考虑。
所以,只考虑$L_{t-1}$,即:
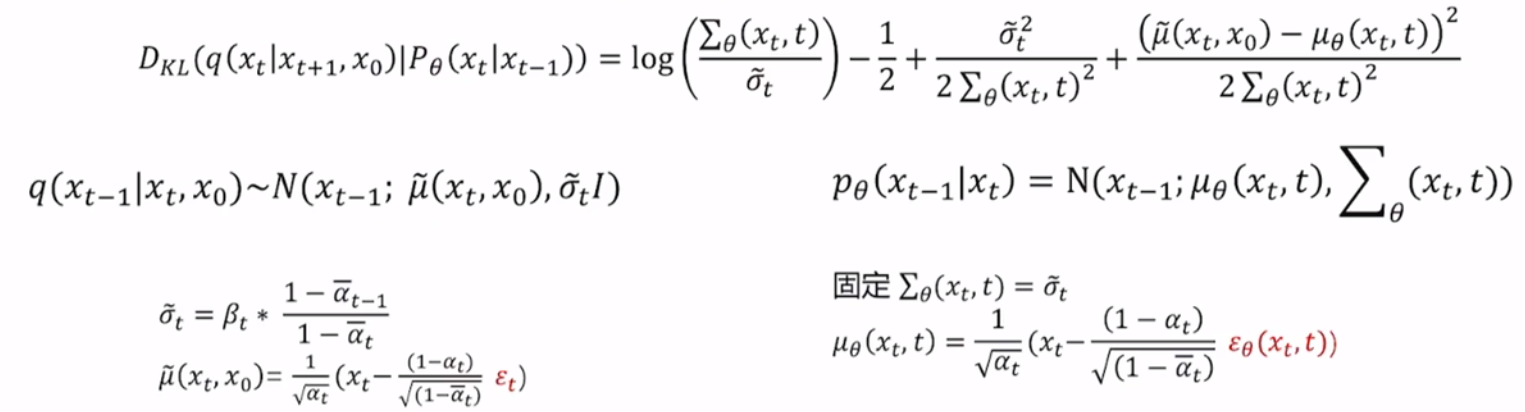
最终就是训练一个去噪模型。
最终的算法:

DDPM代码在DDPM生成人脸代码一节。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号