递归思想

一、递归
什么是递归？
从字面意思来看，递---传递，归---回归。那么从传递开始回归到传递的开始，就是从一个地方出发，回到了出发的地方，就完成了一次循环，
而不断地重复这个循环，就是递归。这里有一个耳熟能详的故事：从前有座山，山里有一座庙，庙里有一个老和尚和小和尚，他们在说故事，
故事是什么呢？从前有座山，山里有一座庙，庙里有一个老和尚和小和尚，他们在说故事，故事是什么呢？从前有座山，山里有一座庙，
庙里有一个老和尚和小和尚，他们在说故事，故事是什么呢？从前有座山，山里有一座庙......等等......

二、经典的递归案例(一)-----斐波那契数列
众所周知：斐波那契数列是[1，1，2，3，5，8，13.....]，就是后一个数是前两项之和，不断地相加。
那么能不能通过python代码来实现，比如说，随便说出一个位置，把该位置对应的数值立马就显示出来，另外还把这之前的斐波那契数列也显示出来
我们先分析这个数列，请看下图这张图

 然后继续看如下的python代码分析

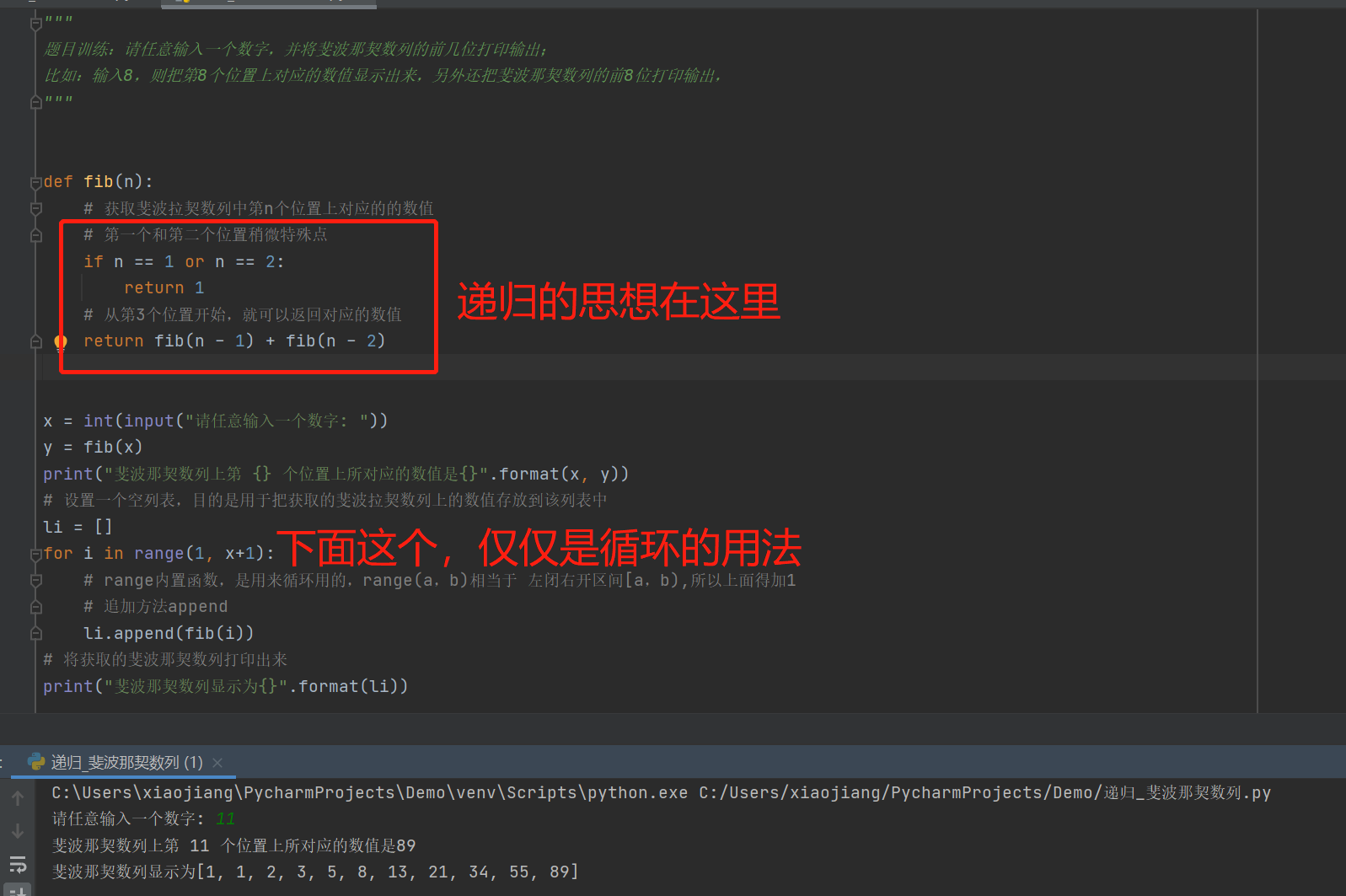
def fib(n):
    # 获取斐波拉契数列中第n个位置上对应的的数值
    # 第一个和第二个位置稍微特殊点
    if n == 1 or n == 2:
        return 1
    # 从第3个位置开始，就可以返回对应的数值
    return fib(n - 1) + fib(n - 2)


x = int(input("请任意输入一个数字: "))
y = fib(x)
print("斐波那契数列上第 {} 个位置上所对应的数值是{}".format(x, y))
# 设置一个空列表，目的是用于把获取的斐波拉契数列上的数值存放到该列表中
li = []
for i in range(1, x+1):
    # range内置函数，是用来循环用的，range(a，b)相当于 左闭右开区间[a，b),所以上面得加1
    # 追加方法append
    li.append(fib(i))
# 将获取的斐波那契数列打印出来
print("斐波那契数列显示为{}".format(li))

三、经典的递归案例(二)-----汉诺塔问题

汉诺塔问题：汉诺塔(Tower of Hanoi)源于印度传说中，大梵天创造世界时造了三根金钢石柱子，其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘
从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。碰到这个问题怎么解？
我们简单分析一下，既然出了这个题，肯定是有解法的，而且会很有规律，这个时候就基本可以用到递归的思想了
解法：是不是，咱们可以这样理解：三根柱子A、B、C；在A柱子上，分别从小到大放了3个盘子(甲乙丙)，现在要求所有的3个盘子从A柱子全部移到B柱子，规则就是：
可以使用柱子C用来临时存放，每次只能移动一个盘子，且每根柱子上不能出现大盘压小盘，只能小的在上面才没有违规，找出移动次数最小的方案。

 这样，甲乙丙三个盘子就顺利的从A柱子上完美的移动到了B柱子上。

上面的图解分析，相信各位应该能看懂。这就是解法，可是有的同学说，假如是四个盘子，五个盘子，怎么办？你这三个盘子太简单了，能不能再示范其他的？

可以，我照样拿出分析来给你看；请各位同学看下图，甲乙丙丁四个盘子，从小到大依次叠放在一起；其实我们刚刚就已经把3个盘子的挪过来了，这个时候，把最上面的3个盘子看作是一个整体

因为它可以经过一系列的步骤，准备的从A柱子挪动到B柱子，于是就有了开始的下图第一行

 由此可见，即使是4个盘子也是可以的；那么同理可推，64个盘子也是一样；只是，你要把除了底部最大的盘子独立之外，其余的63个盘子，看作一个整体，这样就可以照搬刚刚的思路。

这种不断地利用自己本身的循环，就是递归的思想。

以下是我对递归的几点思考：

1、要完成最后一步，那么在完成最后一步之前该做什么？

2、得根据小的例子，发现规律，以小见大；大型递归跟踪分析不可取，拆分最佳

3、递归的优点是能使程序的结构更清晰，更简洁，更容易让人理解；但是缺点是会耗费大量的时间和内存

四、递归的练习

1、1+2+3+...+n的前n项和
2、求n个整数的积
3、已知：数列1,1,2,4,7,13,24,44,...求数列的第 n项

感兴趣的同学可以自己练练手，有助于加深你对递归的理解。