『转载』关于HSL和HSV颜色空间的详细论述
原文转载自 博客园 brave-sailor https://www.cnblogs.com/Free-Thinker/p/4952741.html
目前在计算机视觉领域存在着较多类型的颜色空间(color space)。HSL和HSV是两种最常见的圆柱坐标表示的颜色模型,它重新影射了RGB模型,从而能够视觉上比RGB模型更具有视觉直观性。
HSV颜色空间
HSV(hue,saturation,value)颜色空间的模型对应于圆柱坐标系中的一个圆锥形子集,圆锥的顶面对应于V=1. 它包含RGB模型中的R=1,G=1,B=1 三个面,所代表的颜色较亮。色彩H由绕V轴的旋转角给定。红色对应于 角度0° ,绿色对应于角度120°,蓝色对应于角度240°。在HSV颜色模型中,每一种颜色和它的补色相差180° 。 饱和度S取值从0到1,所以圆锥顶面的半径为1。HSV颜色模型所代表的颜色域是CIE色度图的一个子集,这个 模型中饱和度为百分之百的颜色,其纯度一般小于百分之百。在圆锥的顶点(即原点)处,V=0,H和S无定义, 代表黑色。圆锥的顶面中心处S=0,V=1,H无定义,代表白色。从该点到原点代表亮度渐暗的灰色,即具有不同 灰度的灰色。对于这些点,S=0,H的值无定义。可以说,HSV模型中的V轴对应于RGB颜色空间中的主对角线。 在圆锥顶面的圆周上的颜色,V=1,S=1,这种颜色是纯色。HSV模型对应于画家配色的方法。画家用改变色浓和 色深的方法从某种纯色获得不同色调的颜色,在一种纯色中加入白色以改变色浓,加入黑色以改变色深,同时 加入不同比例的白色,黑色即可获得各种不同的色调。
HSI颜色空间
HSI色彩空间是从人的视觉系统出发,用色调(Hue)、色饱和度(Saturation或Chroma)和亮度 (Intensity或Brightness)来描述色彩。HSI色彩空间可以用一个圆锥空间模型来描述。用这种 描述HIS色彩空间的圆锥模型相当复杂,但确能把色调、亮度和色饱和度的变化情形表现得很清楚。 通常把色调和饱和度通称为色度,用来表示颜色的类别与深浅程度。由于人的视觉对亮度的敏感 程度远强于对颜色浓淡的敏感程度,为了便于色彩处理和识别,人的视觉系统经常采用HSI色彩空间, 它比RGB色彩空间更符合人的视觉特性。在图像处理和计算机视觉中大量算法都可在HSI色彩空间中 方便地使用,它们可以分开处理而且是相互独立的。因此,在HSI色彩空间可以大大简化图像分析 和处理的工作量。HSI色彩空间和RGB色彩空间只是同一物理量的不同表示法,因而它们之间存在着 转换关系。
HSI 色彩模型是从人的视觉系统出发,用 H 代表色相 (Hue)、S 代表饱和度 (Saturation) 和 I 代表亮度 (Intensity) 来描述色彩。饱和度与颜色的白光光量刚好成反比,它可以说是一个颜色鲜明与否的指标。因此如果我们在显示器上使用 HIS 模型来处理图像,将能得到较为逼真的效果。
色相 (Hue):指物体传导或反射的波长。更常见的是以颜色如红色,橘色或绿色来辨识,取 0 到 360 度的数值来衡量。
饱和度 (Saturation):又称色度,是指色彩的强度或纯度。饱和度代表灰色与色调的比例,并以 0% (灰色) 到 100% (完全饱和) 来衡量。
亮度 (Intensity):是指颜色的相对明暗度,通常以 0% (黑色) 到 100% (白色) 的百分比来衡量。
HSL代表色调(Hue),饱和度(Saturation)和亮度(Lightness),通常也称为HLS。HSV代表色调,饱和度和值(Value)。注意HSL 和HSV的两个H的含义是相同的,而饱和度的定义是不同的,虽然都叫饱和度,从后面的定义可以看出二者的不同。
HSL 和 HSV 二者都把颜色描述在圆柱体内的点,这个圆柱的中心轴取值为自底部的黑色到顶部的白色而在它们中间是的灰色,绕这个轴的角度对应于“色相”,到这个轴的距离对应于“饱和度”,而沿着这个轴的距离对应于“亮度”,“色调”或“明度”。 HSV 以人类更熟悉的方式封装了关于颜色的信息:“这是什么颜色?深浅如何?明暗如何?”。HSL 颜色空间类似于 HSV,在某些方面甚至比它还好。HSL的模型为双圆锥形状。
这两种表示在用目的上类似,但在方法上有区别。二者在数学上都是圆柱,但 HSV(色相,饱和度,明度)在概念上可以被认为是颜色的倒圆锥体(黑点在下顶点,白色在上底面圆心),HSL 在概念上表示了一个双圆锥体和圆球体(白色在上顶点,黑色在下顶点,最大横切面的圆心是半程灰色)。HSV 模型在 1978 年由埃尔维?雷?史密斯创立。下图给出了HSL和HSV的圆柱模型。
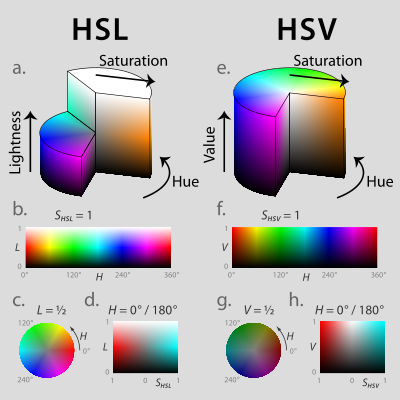
用圆锥模型如图:


在圆锥上,角度代表色调H,饱和度S表示为点到中心竖线的距离,而亮度或者值V用中心竖线表示。红色的角度为0度,依次为黄色、绿色、青色、蓝色、橙色。连续两种颜色的角度相差60度。
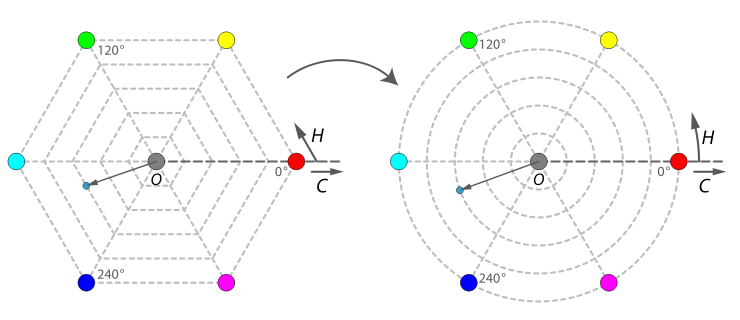
下图给出了一个RGB到HS平面的影射例子。
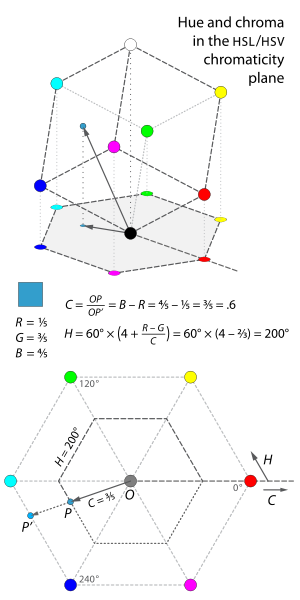
下表给出了RGB到HSL和HSV的影射样例。
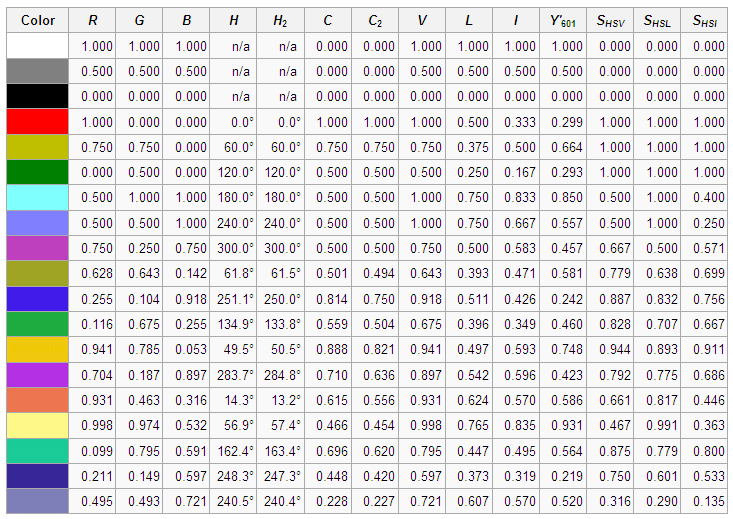
那么如何从RGB到HSL和HSV的转换呢?利用下面的步骤就可以实现从RGB到HSL和HSV的转换。
已知一点的R、G、B,计算最大值和最小值

计算H:
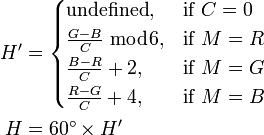
计算L和V:
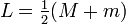

计算S:
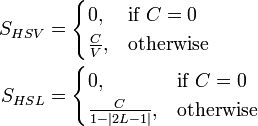
上面的公式实现了从RGB到HSL和HSV的转换。那么当采用Opencv的彩色空间转化函数cvCvtColor(orgFrame,destFrame, CV_BGR2HSV),如果图像的数据类型为8位字符型时,则H、S、V都量化到整数{0~255},可以看出H的精度不是很高。
当在HSL和HSV空间进行处理后,需要转换到RGB,可以采用下面的公式计算RGB。
先讨论HSV到RGB的转换,这里H ∈ [0°, 360°], S ∈ [0, 1], V ∈ [0, 1]。转换公式如下:
计算C

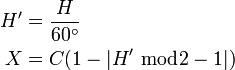
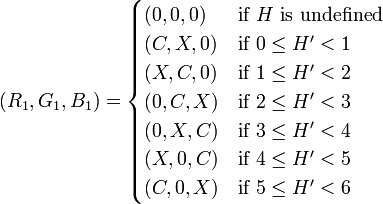
最后得到:
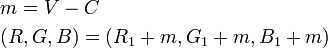
从HSL到RGB的转换。这里H ∈ [0°, 360°], S ∈ [0, 1], V ∈ [0, 1]。转换公式如下:
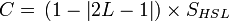
然后:

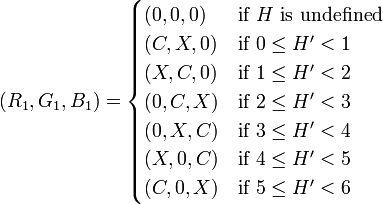
最后得到:

展示的 RGB 值的范围是 0.0 到 1.0。
下面用C实现RGB到HSV的转换,采用宏定义的方式。
1 // ///////////////////////////////////////////////////////////////////// 2 // 3 // cvlab.net 4 // C/C++ Macro RGB to HSV 5 #define PIX_RGB_TO_HSV_COMMON(R,G,B,H,S,V,NORM) \ 6 if((B > G) && (B > R)) \ 7 { \ 8 V = B; \ 9 if(V != 0) \ 10 { \ 11 double min; \ 12 if(R > G) min = G; \ 13 else min = R; \ 14 const double delta = V - min; \ 15 if(delta != 0) \ 16 { S = (delta/V); H = 4 + (R - G) / delta; } \ 17 else \ 18 { S = 0; H = 4 + (R - G); } \ 19 H *= 60; if(H < 0) H += 360; \ 20 if(!NORM) V = (V/255); \ 21 else S *= (100); \ 22 } \ 23 else \ 24 { S = 0; H = 0;} \ 25 } \ 26 else if(G > R) \ 27 { \ 28 V = G; \ 29 if(V != 0) \ 30 { \ 31 double min; \ 32 if(R > B) min = B; \ 33 else min = R; \ 34 const double delta = V - min; \ 35 if(delta != 0) \ 36 { S = (delta/V); H = 2 + (B - R) / delta; } \ 37 else \ 38 { S = 0; H = 2 + (B - R); } \ 39 H *= 60; if(H < 0) H += 360; \ 40 if(!NORM) V = (V/255); \ 41 else S *= (100); \ 42 } \ 43 else \ 44 { S = 0; H = 0;} \ 45 } \ 46 else \ 47 { \ 48 V = R; \ 49 if(V != 0) \ 50 { \ 51 double min; \ 52 if(G > B) min = B; \ 53 else min = G; \ 54 const double delta = V - min; \ 55 if(delta != 0) \ 56 { S = (delta/V); H = (G - B) / delta; } \ 57 else \ 58 { S = 0; H = (G - B); } \ 59 H *= 60; if(H < 0) H += 360; \ 60 if(!NORM) V = (V/255); \ 61 else S *= (100); \ 62 } \ 63 else \ 64 { S = 0; H = 0;} \ 65 } 66 67 // ////////////////////////////////////////////////////////////////// 68 // 69 // cvlab.net 70 // C/C++ Macro HSV to RGB 71 #define PIX_HSV_TO_RGB_COMMON(H,S,V,R,G,B) \ 72 if( V == 0 ) \ 73 { R = 0; G = 0; B = 0; } \ 74 else if( S == 0 ) \ 75 { \ 76 R = V; \ 77 G = V; \ 78 B = V; \ 79 } \ 80 else \ 81 { \ 82 const double hf = H / 60.0; \ 83 const int i = (int) floor( hf ); \ 84 const double f = hf - i; \ 85 const double pv = V * ( 1 - S ); \ 86 const double qv = V * ( 1 - S * f ); \ 87 const double tv = V * ( 1 - S * ( 1 - f ) ); \ 88 switch( i ) \ 89 { \ 90 case 0: \ 91 R = V; \ 92 G = tv; \ 93 B = pv; \ 94 break; \ 95 case 1: \ 96 R = qv; \ 97 G = V; \ 98 B = pv; \ 99 break; \ 100 case 2: \ 101 R = pv; \ 102 G = V; \ 103 B = tv; \ 104 break; \ 105 case 3: \ 106 R = pv; \ 107 G = qv; \ 108 B = V; \ 109 break; \ 110 case 4: \ 111 R = tv; \ 112 G = pv; \ 113 B = V; \ 114 break; \ 115 case 5: \ 116 R = V; \ 117 G = pv; \ 118 B = qv; \ 119 break; \ 120 case 6: \ 121 R = V; \ 122 G = tv; \ 123 B = pv; \ 124 break; \ 125 case -1: \ 126 R = V; \ 127 G = pv; \ 128 B = qv; \ 129 break; \ 130 default: \ 131 LFATAL("i Value error in Pixel conversion, Value is %d",i); \ 132 break; \ 133 } \ 134 } \ 135 R *= 255.0F; \ 136 G *= 255.0F; \ 137 B *= 255.0F; 138 139 140 ==============================================================================================================
在图像和视频处理中,经常需要在颜色空间YUV和RGB间转换。下面介绍如何在这两种格式间进行转换。
YUV可以实现较高的数据压缩率,这主要是由于U、V分量可以实现高度压缩。而RGB888采用8bits分别表示R、G、B三个分量。黑色:R = G = B = 0;白色:R = G = B = 255。
RGB888的采样格式为4:4:4。
转换RGB888为YUV
转换公式为:
1 Y = ( ( 66 * R + 129 * G + 25 * B + 128) >> 8) + 16 2 U = ( ( -38 * R - 74 * G + 112 * B + 128) >> 8) + 128 3 V = ( ( 112 * R - 94 * G - 18 * B + 128) >> 8) + 128
上述公式的结果为8bit,但中间结果需要16bits的精度。
转换YUV到RGB888
转换公式为:
1 C = Y - 16 2 D = U - 128 3 E = V - 128
利用上述结果,然后计算RGB,1 R = clip(( 298 * C + 409 * E + 128) >> 8) 2 G = clip(( 298 * C - 100 * D - 208 * E + 128) >> 8) 3 B = clip(( 298 * C + 516 * D + 128) >> 8)
这里clip()
表示限制RGB的值的范围在(0~255)。这些转换结果精度仍然为8bit,但是中间结果需要16bits精度。
注意当结果超出范围时,需要进行饱和截止。
如何要转换4:2:0 或者 4:2:2 YUV,需要首先转换YUV为4:4:4格式的YUV,然后再转换4:4:4 YUV为RGB888。