Educational Codeforces Round 170 (Rated for Div. 2)
B. Binomial Coefficients, Kind Of
题目大意: 先是给了你一份程序代码,然后嘞,输入了两行,一行是 n1、n2、……nt,第二行是k1、k2、……kt。问你C[nx][kx]的答案。
input:
7
2 5 5 100000 100000 100000 100000
1 2 3 1 33333 66666 99999output:
2
4
8
2
326186014
984426998
303861760分析: 是一个打表找规律的题(不知道,为什么赛时压根没想到打表…… 一直在纠结题目代码什么意思 -_- )打表就按照题目给的代码就行了。
打表代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 5e3 + 100;
int cc[maxn][maxn];
int main(){
int n;
cin >> n;
for (int i = 0;i < n;i++){
cc[i][0] = 1;
cc[i][1] = 1;
for (int j = 1;j < n;j++) {
cc[i][j] = cc[i][j - 1] + cc[i - 1][j - 1];
}
}
for (int i = 1;i <= n ;i++){
cout << i << " ----- " << cc[i][i] << endl;
}
return 0;
}打表结果:
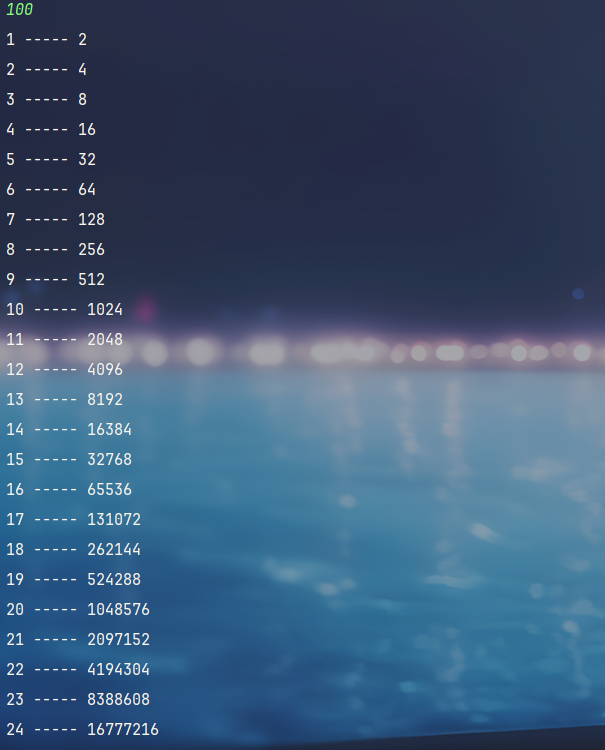
结果很明显 第几组就是 2的第几组次方 这时候再看样例输出是怎么构造的:
第一组:(2,1) -> 2
第二组:(5,2)-> 4
第三组:(5,3)-> 8
第四组:(100000,1) -> 2
不难发现,每组答案是选择了当前组Ni和Ki的最小值(因为Ni>=Ki,所以只用取Ki就行了) 当作2的次方的 ,所以快速幂,求一下就行了;
AC代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll const maxn = 2e6 + 100;
const ll mod = 1e9 + 7;
int cc[maxn];
ll pw(ll n,ll x){
ll ans = 1;
n = n % mod;
while (x > 0){
if (x & 1)ans = ans * n % mod;
x >>= 1;
n = n * n % mod;
}
return ans % mod;
}
int main(){
int n;
cin >> n;;
for (int i = 0;i < n;i++){
cin >> cc[i];
}
for (int i = 0,num;i < n;i++){
cin >> num;
cout << pw(2,num) % mod << endl;
}
return 0;
}
C. New Game
题目大意: 给你n张卡片(每张都有一个编号,且同一个编号的卡片数量不唯一)和一个阈值k,每次在当前卡片里面选一张,这张的编号要么和上一次选的一样,要么只是大一号,选完某张,某张就从卡组里面消失了,更重要的是,选择的卡片的不同种类数目不能大于k,让你求在不违反规则的条件下能选的最多卡片数量。
分析:
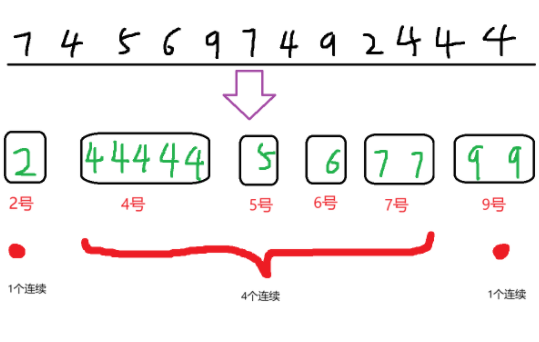
既然只能选择比上一个大一或者相同的编号,那么这不就是只能挨着选嘛,既然是挨着,那么思路不妨往“连续”上面靠。对于相同的编号,我们无论选多少次,对当前不同种类数逼近k的影响只有1次(第一次选的时候)因为k是不同种类的数量,这是很好想的一点。所以我们可以将每个编号有多少个统计出来,只对不同编号去分析。
又因为在不同编号里面只能选择比上一个大一的号码,即只能选连续加一的,遇到不连续的就不能选了,所以我们又可以将每段连续的编号分离出来 上图已经画出来了。
那么如何统计答案呢?请看下图
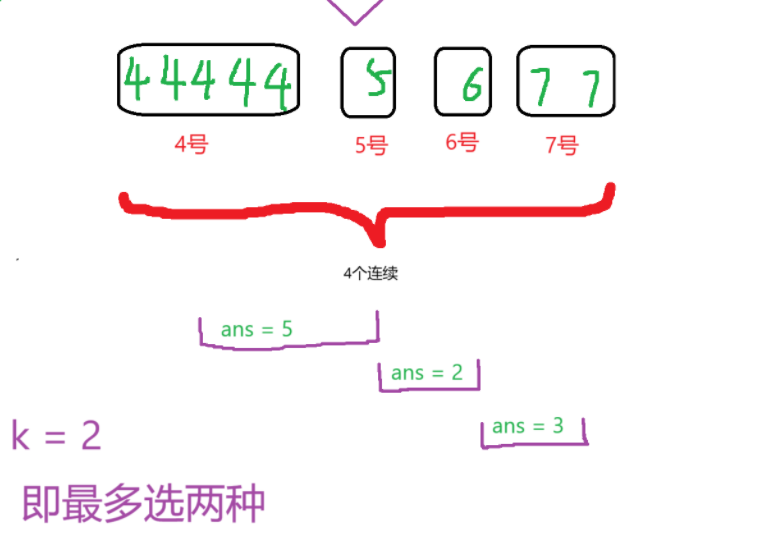
对于这里段连续的编号(4、5、6、7)我们可以,遍历长度为k的区间就能获取到这块儿连续段的答案,那么总答案,就是将所有卡号码分成多个连续段,再以最大为k的长度去遍历所有连续段的号码,取一个最大值即可,(注意 如果当前连续段的长度小于等于k的话只去要取当前段所有种类数量和即可。)
AC代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll const maxn = 2e6 + 100;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t,n,k;
cin >> t;
while (t--){
map<int,int> mp;//维护每个编号出现了多少次
vector<int> num;//维护编号集合(去重过)
stack<vector<pair<int,int> > >st;//维护多少个连续段,每个段里面维护了,每个编号和编号的数量
cin >> n >> k;
for (int i = 1;i <= n;i++){
int id;
cin >> id;
mp[id] += 1;
}
for (auto &c : mp){
num.push_back(c.first);
}
//将连续的段分离提取
st.push(vector<pair<int,int > >(1,make_pair(num.front(),mp[num.front()])));//先放一个进去
for (int i = 1;i < num.size();i++){
int id = num[i],v = mp[num[i]];//编号,编号数量
if (id - st.top().back().first == 1){//是否连续
st.top().push_back(make_pair(id,v));//连续就直接放进来
}
else {//不然就另开一个放进去
st.push(vector<pair<int,int > >(1,make_pair(id,v)));
}
}
ll ans = 0;//记录答案
while (!st.empty()){
vector<ll> sum(st.top().size() + 2,0);//维护每段里面每个编号数量的前缀和(优化查询)
for (int i = 0,j = 1;i < st.top().size();i++,j++){
sum[j] = sum[j - 1] + st.top()[i].second;
}
if (k >= st.top().size()){//如果这段连续的长度不大于k
ans = max(ans,sum[st.top().size()]);
}
else {//如果大于k就要遍历所有长度为k的区间了
for (int i = 0,j = 1;i <= st.top().size() - k;i++,j++){
ans =max(ans,sum[j + k - 1] - sum[j - 1]);
}
}
st.pop();
}
cout << ans << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号