python不用库求解根号N

问题描述

我们需要在不使用库的情况下求解\(\sqrt{n}\)。

方法一：二分法

令\(y=\sqrt{x}\)，问题转换为求得y，使得\(y^{2}-x=0, (x>=0)\)。我们令\(f(y)=y^{2}-x\)。注意到:

\[f(0)-x<=0 \]

\[f(x+1)=(x+1)^{2}-x=(x+\frac{1}{2})^{2}+\frac{7}{4}>0 \]

我们可以在区间\((0,x+1)\)上必可以得到一个解\(y_{0}\)，使得\(y_{0}^{2}-x=0\)。
代码如下：

def cal(x, err):
    """
    y = x**(1/2)
    y**2-x=0
    f(y)=y**2-x
    f(0)=-x小于等于0
    f(x+1)=(x+1)**2-x=x**2+2x+2-x=x**2+x+2=(x+1/2)**2+7/4>0
    """
    left = 0
    right = x + 1
    mid = left
    while abs(right - left) > err:
        mid = (left + right) / 2
        y = mid * mid - x
        if y > 0:
            right = mid
        else:
            left = mid
    print(mid)
    return mid
cal(4, 1e-6)
# 2.0000000000436557

方法二：使用泰勒公式

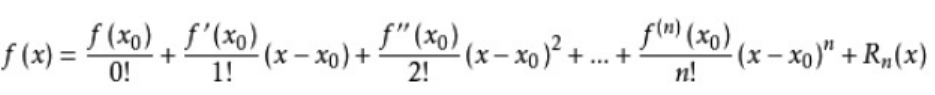
记\(f(y)=y_{2}-x\)，根据泰勒公式展开到一阶：

\[f(y)=f(y_{0})+f^{'}(y_{0})(y-y_{0}) \]

令\(f(y)=0\)继而可以求得：

\[y=y_{0}-\frac{f_{y_{0}}}{f^{'}(y_{0})} \]

假设\(y_{1}=y\)，那么会发现\(y_{1}\)会比\(y_{0}\)更接近于最终答案，因此，我们可以通过以下递推公式求解：

\[y_{n+1} = y_{n}-\frac{f(y_{n})}{f^{'}(y_{n})} \]

代码如下：

def cal2(x):
    """
    f(x)=f(x0)+f'(x0)(x-x0)+(f''(x0)(x-x0)**2/2!)+......+err
    """
    y = 1
    for i in range(100):
        y = y - (y * y - x) / (y * 2)
    print(y)
    return y

cal2(4)
# 2.0