实战-电力窃露漏电用户自动识别

问题描述：判断用户是否窃漏电

问题解决：二分类问题

缺失值：拉格朗日插值法进行填充

使用的特征：电量趋势下降指标、线损指标、警告类指标

这里使用的数据来<python数据分析与实战第六章>

数据：

代码实现：

1、加载数据

import pandas as pd
from random import shuffle

datafile = path + 'chapter6/model.xls'
data = pd.read_excel(datafile)

2、划分训练集和测试集

#data = data.as_matrix() 旧版本的pandas是这么使用的，将dataframe转换为矩阵
data = data.iloc[:,:].values #新版本这么使用
shuffle(data)

p = 0.8 #设置训练数据比例
train = data[:int(len(data)*p),:]
test = data[int(len(data)*p):,:]

3、使用keras定义模型

from keras.models import Sequential #导入神经网络初始化函数
from keras.layers.core import Dense, Activation #导入神经网络层函数、激活函数

netfile = path + 'chapter6/net.model' #构建的神经网络模型存储路径

net = Sequential() #建立神经网络
net.add(Dense(3, 10)) #添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu')) #隐藏层使用relu激活函数
net.add(Dense(10, 1)) #添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid')) #输出层使用sigmoid激活函数
net.compile(loss = 'binary_crossentropy', optimizer = 'adam', class_mode = "binary") #编译模型，使用adam方法求解

net.fit(train[:,:3], train[:,3], nb_epoch=100, batch_size=1) #训练模型，循环100次
net.save_weights(netfile) #保存模型

由于keras版本导致的错误：

常见错误（均是因为keras版本改动）

• TypeError: Dense can accept only 1 positional arguments ('units',), but you passed the following positional arguments: [23, 34]
• 解决方法：在Dense中写好参数名称改为Dense(input_dim=23,units=34)
• ValueError: ('Some keys in session_kwargs are not supported at this time: %s', dict_keys(['class_mode']))
解决方法：模型编译代码中去掉class_mode这一属性
• UserWarning: The nb_epoch argument in fit has been renamed epochs


  解决方法：

  修改代码中的“nb_epoch”为“epochs”即可

修改后的代码：

from keras.models import Sequential #导入神经网络初始化函数
from keras.layers.core import Dense, Activation #导入神经网络层函数、激活函数

netfile = path + 'chapter6/net.model' #构建的神经网络模型存储路径

net = Sequential() #建立神经网络
net.add(Dense(input_dim=3, units=10)) #添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu')) #隐藏层使用relu激活函数
net.add(Dense(input_dim=10, units=1)) #添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid')) #输出层使用sigmoid激活函数
net.compile(loss = 'binary_crossentropy', optimizer = 'adam') #编译模型，使用adam方法求解

net.fit(train[:,:3], train[:,3], epochs=100, batch_size=1) #训练模型，循环100次
net.save_weights(netfile) #保存模型

部分结果：

Epoch 97/100
232/232 [==============================] - 1s 3ms/step - loss: 0.3171
Epoch 98/100
232/232 [==============================] - 1s 3ms/step - loss: 0.3196
Epoch 99/100
232/232 [==============================] - 1s 3ms/step - loss: 0.3194
Epoch 100/100
232/232 [==============================] - 1s 3ms/step - loss: 0.3144

我们也可以训练时加入更多的评价指标：（二分类指标）

具体的评价指标的使用可参考文档：

https://keras.io/api/metrics/classification_metrics/#precision-class

import tensorflow as tf
import numpy as np
#精确率评价指标
from keras.models import Sequential #导入神经网络初始化函数
from keras.layers.core import Dense, Activation #导入神经网络层函数、激活函数

netfile = path + 'chapter6/net.model' #构建的神经网络模型存储路径

net = Sequential() #建立神经网络
net.add(Dense(input_dim=3, units=10)) #添加输入层（3节点）到隐藏层（10节点）的连接
net.add(Activation('relu')) #隐藏层使用relu激活函数
net.add(Dense(input_dim=10, units=1)) #添加隐藏层（10节点）到输出层（1节点）的连接
net.add(Activation('sigmoid')) #输出层使用sigmoid激活函数

net.compile(loss = 'binary_crossentropy', optimizer = 'adam', 
            metrics=['accuracy',
            tf.keras.metrics.Precision(),
            tf.keras.metrics.Recall()]) #编译模型，使用adam方法求解

net.fit(train[:,:3], train[:,3], epochs=100, batch_size=1) #训练模型，循环1000次
net.save_weights(netfile) #保存模型

部分结果：

Epoch 97/100
232/232 [==============================] - 1s 4ms/step - loss: 0.1729 - accuracy: 0.9526 - precision: 0.8902 - recall: 0.8770
Epoch 98/100
232/232 [==============================] - 1s 4ms/step - loss: 0.1740 - accuracy: 0.9526 - precision: 0.8908 - recall: 0.8774
Epoch 99/100
232/232 [==============================] - 1s 4ms/step - loss: 0.1693 - accuracy: 0.9569 - precision: 0.8910 - recall: 0.8780
Epoch 100/100
232/232 [==============================] - 1s 4ms/step - loss: 0.1750 - accuracy: 0.9526 - precision: 0.8915 - recall: 0.8783

对模型进行验证：

scores = net.evaluate(test[:,:3], test[:,3], verbose=0)
for i in range(1,len(net.metrics_names)):
  print("%s: %.2f%%" % (net.metrics_names[i], scores[i]*100)) # 打印出验证集准确率

accuracy: 88.14%

precision: 89.14%

recall: 87.85%

使用模型进行预测：这里注意有两个api，一个得到的是概率值，另一个得到的是类别：

使用predict()得到的是概率值：这里将其用round进行四舍五入后进行展开。

predict_result = tf.round(net.predict(test[:,:3]).reshape(len(test)))
with tf.Session() as sess:
  print(predict_result.eval())

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 0. 0. 1. 0. 0. 1. 1. 1. 1. 0. 0. 1. 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 1. 0. 0. 0.]

使用predict_classes()得到的是类别：

predict_result2 = net.predict_classes(test[:,:3]).reshape(len(test))
predict_result2 

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0], dtype=int32)

打印一下真实的标签：

y_true = np.array(test[:,3])

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

4、评价指标的计算方式以及混淆矩阵

我们可以直接通过sklearn api来计算评价指标：

from sklearn.metrics import classification_report
target_names = ['no','yes']
print(classification_report(test[:,3],predict_result2,target_names=target_names))

结果：

              precision    recall  f1-score   support

          no       0.98      0.88      0.93        50
         yes       0.57      0.89      0.70         9

    accuracy                           0.88        59
   macro avg       0.77      0.88      0.81        59
weighted avg       0.92      0.88      0.89        59

或者我们可以通过混淆矩阵自己来计算：首先是获得混淆矩阵

from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(test[:,3], predict_result2)
print(cnf_matrix)

#行、列的索引就是标签id，这里有两类，用0,1,表示
[[44  6]
 [ 1  8]]

混淆矩阵中的四个值分别代表TP、FP、TN、PN

根据混淆矩阵，我们可以计算二分类评价指标：（标签为1的是正样本，因此TP是[1][1]）

TP=cnf_matrix[1][1] #预测为正的真实标签为正
FP=cnf_matrix[0][1] #预测为正的真实标签为负
FN=cnf_matrix[1][0] #预测为负的真实标签为正
TN=cnf_matrix[0][0] #预测为负的真实标签为负
accuracy=(TP+TN)/(TP+FP+FN+TN)
precision=TP/(TP+FP)
recall=TP/(TP+FN)
f1score=2 * precision * recall/(precision + recall)
print(accuracy,precision,recall,f1score)

0.8813559322033898 0.5714285714285714 0.8888888888888888 0.6956521739130435

这也上面api计算的yes的评价指标的值一致。

5、绘制混淆矩阵

import matplotlib.pyplot as plt 
%matplotlib inline
def cm_plot(y, yp, labels_name):
  
  from sklearn.metrics import confusion_matrix #导入混淆矩阵函数

  cm = confusion_matrix(y, yp) #混淆矩阵
  
  plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
  plt.colorbar() #颜色标签
  num_local = np.array(range(len(labels_name))) 
  plt.xticks(num_local, labels_name)    # 将标签印在x轴坐标上
  plt.yticks(num_local, labels_name)    # 将标签印在y轴坐标上

  for x in range(len(cm)): #数据标签
    for y in range(len(cm)):
      plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')

  plt.ylabel('True label') #坐标轴标签
  plt.xlabel('Predicted label') #坐标轴标签
  return plt
cm_plot(test[:,3],predict_result2,['no', 'yes']).show()

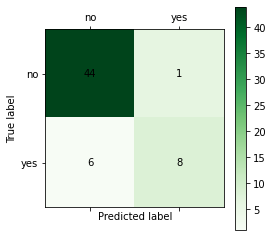
6、二分类其他评价指标（这两个我重新在colab上运行的，因此数据和上面不一样）

ROC曲线：

横坐标：假正率（False positive rate， FPR），预测为正但实际为负的样本占所有负例样本的比例；

FPR = FP / ( FP +TN)   

纵坐标：真正率（True positive rate， TPR），这个其实就是召回率，预测为正且实际为正的样本占所有正例样本的比例。

TPR = TP / ( TP+ FN) 

AUC：就是roc曲线和横坐标围城的面积。

如何绘制？

对于二值分类问题，实例的值往往是连续值，通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。上述中我们直接利用四舍五入来区分正类和负类。因此，可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。ROC curve经过(0,0) (1,1)，实际上(0,0)和(1,1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于(0,0)和(1,1)连线的上方，

代码实现：

from sklearn.metrics import roc_curve, auc
# 为每个类别计算ROC曲线和AUC
predict_res=net.predict(test[:,:3]).reshape(len(test))
fpr,tpr,threholds=roc_curve(test[:,3],predict_res,pos_label=1)
roc_auc=auc(fpr,tpr)
plt.plot(fpr,tpr,linewidth=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

绘制Precision-Recall曲线：

from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
precision,recall,_ = precision_recall_curve(test[:,3],predict_res,pos_label=1)
average_precision = average_precision_score(test[:,3],predict_res,pos_label=1)
plt.plot(recall, precision,label='Precision-recall curve of class (area = {1:0.2f})'.format(i, average_precision))
plt.xlabel('Recall', fontsize=16)
plt.ylabel('Precision',fontsize=16)
plt.title('Extension of Precision-Recall curve to 2-class',fontsize=16)
plt.legend(loc="upper right")#legend 是用于设置图例的函数
plt.show()

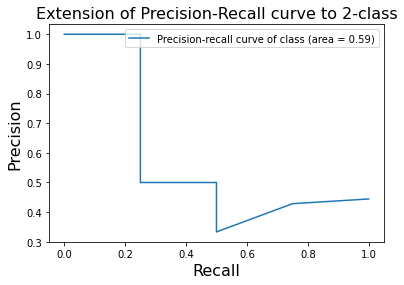
关于二分类评价指标网上已经有很多讲解的很清楚的了，就不仔细讲了，还是注重实际的代码。本来是应该对比不同的模型的，结果搞成了讲解二分类指标了。。。 

 

参考：

《python数据分析与挖掘实战》 

https://www.cnblogs.com/liweiwei1419/p/9870034.html

https://blog.csdn.net/weixin_39541558/article/details/82708832