sklearn自带的数据集以及生成数据
1、自带的数据集
sklearn自动了下面几种数据用于算法练习。
load_boston([return_X_y]) 加载波士顿房价数据;用于回归问题
load_iris([return_X_y]) 加载iris 数据集;用于分类问题
load_diabetes([return_X_y]) 加载糖尿病数据集;用于回归问题
load_digits([n_class, return_X_y]) 加载手写字符集;用于分类问题
load_linnerud([return_X_y]) 加载linnerud 数据集;用于多元回归问题
波士顿房价数据,回归使用。样本数据集的特征默认是一个(506, 13)大小的矩阵,样本值是一个包含506个数值的向量。
# 房价数据 from sklearn.datasets import load_boston from sklearn import linear_model boston = load_boston() data=boston.data target = boston.target print(data.shape) print(target.shape) print('系数矩阵:\n',linear_model.LinearRegression().fit(data,target).coef_)
iris花卉数据,分类使用。样本数据集的特征默认是一个(150, 4)大小的矩阵,样本值是一个包含150个类标号的向量,包含三种分类标号。
# 花卉数据 from sklearn.datasets import load_iris from sklearn import svm iris = load_iris() data=iris.data target = iris.target print(data.shape) print(target.shape) print('svm模型:\n',svm.SVC().fit(data,target))
糖尿病数据集,回归使用。样本数据集的特征默认是一个(442, 10)大小的矩阵,样本值是一个包含442个数值的向量。
# 糖尿病数据集 from sklearn.datasets import load_diabetes from sklearn import linear_model diabetes = load_diabetes() data=diabetes.data target = diabetes.target print(data.shape) print(target.shape) print('系数矩阵:\n',linear_model.LinearRegression().fit(data,target).coef_)
手写体数据,分类使用。每个手写体数据使用8*8的矩阵存放。样本数据为(1797, 64)大小的数据集。
# # ===========手写体数据=========== from sklearn.datasets import load_digits import matplotlib.pyplot as plt # 画图工具 digits = load_digits() data=digits.data print(data.shape) plt.matshow(digits.images[3]) # 矩阵像素点的样式显示3 # plt.imshow(digits.images[3]) # 图片渐变的样式显示3 # plt.gray() # 图片显示为灰度模式 plt.show()
linnerud数据集,多元回归使用。样本数据集的特征默认是一个(20, 3)大小的矩阵,样本值也是(20, 3)大小的矩阵。也就是3种特征,有3个输出结果,所以系数矩阵w为(3, 3)
# # ===========多元回归=========== from sklearn.datasets import load_linnerud from sklearn import linear_model linnerud = load_linnerud() data=linnerud.data target = linnerud.target print(data.shape) print(target.shape) print('系数矩阵:\n',linear_model.LinearRegression().fit(data,target).coef_)
2、加载图像
# 图像样本数据集 from sklearn.datasets import load_sample_image import matplotlib.pyplot as plt # 画图工具 img=load_sample_image('flower.jpg') # 加载sk自带的花朵图案 plt.imshow(img) plt.show()
3、生成自定义分类数据集
sklearn.datasets.make_classification(n_samples=100, n_features=20, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True,shift=0.0, scale=1.0, shuffle=True, random_state=None)
通常用于分类算法。
n_features :特征个数= n_informative + n_redundant + n_repeated
n_informative:多信息特征的个数
n_redundant:冗余信息,informative特征的随机线性组合
n_repeated :重复信息,随机提取n_informative和n_redundant 特征
n_classes:分类类别
n_clusters_per_class :某一个类别是由几个cluster构成的
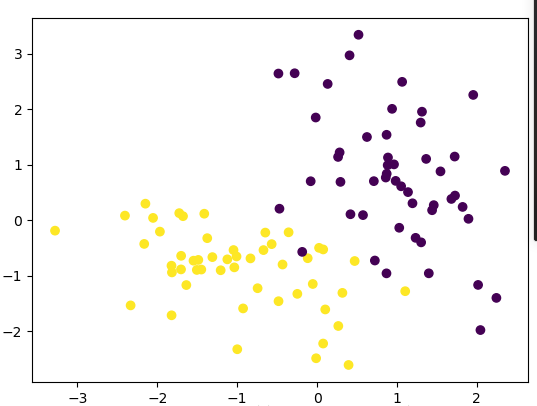
# # ===========生成分类样本数据集=========== from sklearn import datasets import matplotlib.pyplot as plt # 画图工具 data,target=datasets.make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0,n_repeated=0, n_classes=2, n_clusters_per_class=1) print(data.shape) print(target.shape) plt.scatter(data[:,0],data[:,1],c=target) plt.show()
这里生成的数据集图如下,由于每次生成的数据都不一样,所以读者看到的图片和这里也不一样的
4、生成其它分类样本的函数
make_blobs函数会根据用户指定的特征数量、中心点数量、范围等来生成几类数据,这些数据可用于测试聚类算法的效果。
sklearn.datasets.make_blobs(n_samples=100, n_features=2, centers=3, cluster_std=1.0, center_box=(-10.0, 10.0), shuffle=True, random_state=None)
其中:
n_samples是待生成的样本的总数。
n_features是每个样本的特征数。
centers表示类别数。
cluster_std表示每个类别的方差,例如我们希望生成2类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0]。
make_gaussian_quantiles函数利用高斯分位点区分不同数据
sklearn.datasets.make_hastie_10_2(n_samples=12000, random_state=None)
make_hastie_10_2函数利用Hastie算法,生成2分类数据
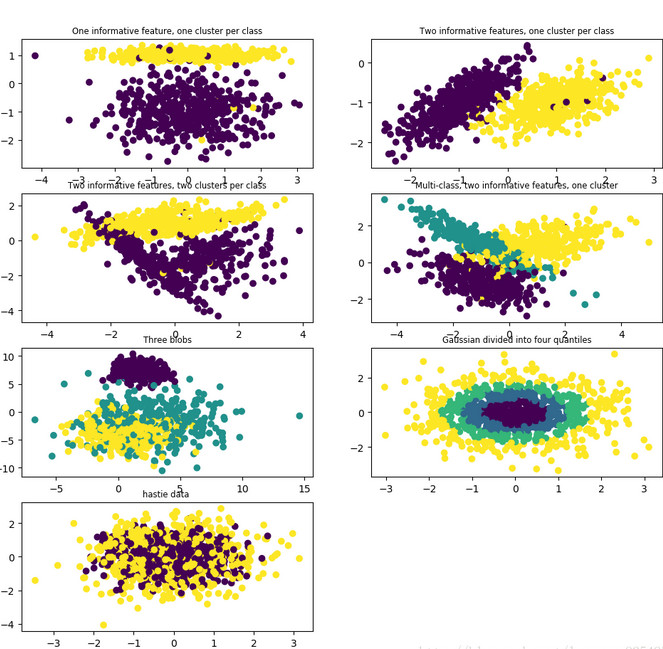
下面我们通过代码的比较一下这些样本数据的生成。
import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.datasets import make_blobs from sklearn.datasets import make_gaussian_quantiles from sklearn.datasets import make_hastie_10_2 plt.figure(figsize=(10, 10)) plt.subplots_adjust(bottom=.05, top=.9, left=.05, right=.95) plt.subplot(421) plt.title("One informative feature, one cluster per class", fontsize='small') X1, Y1 = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=1,n_clusters_per_class=1) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.subplot(422) plt.title("Two informative features, one cluster per class", fontsize='small') X1, Y1 = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2,n_clusters_per_class=1) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.subplot(423) plt.title("Two informative features, two clusters per class", fontsize='small') X2, Y2 = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2) plt.scatter(X2[:, 0], X2[:, 1], marker='o', c=Y2) plt.subplot(424) plt.title("Multi-class, two informative features, one cluster",fontsize='small') X1, Y1 = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2,n_clusters_per_class=1, n_classes=3) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.subplot(425) plt.title("Three blobs", fontsize='small') # 1000个样本,2个属性,3种类别,方差分别为1.0,3.0,2.0 X1, Y1 = make_blobs(n_samples=1000, n_features=2, centers=3,cluster_std=[1.0,3.0,2.0]) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.subplot(426) plt.title("Gaussian divided into four quantiles", fontsize='small') X1, Y1 = make_gaussian_quantiles(n_samples=1000, n_features=2, n_classes=4) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.subplot(427) plt.title("hastie data ", fontsize='small') X1, Y1 = make_hastie_10_2(n_samples=1000) plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1) plt.show()
5、自定义生成圆形和月型数据
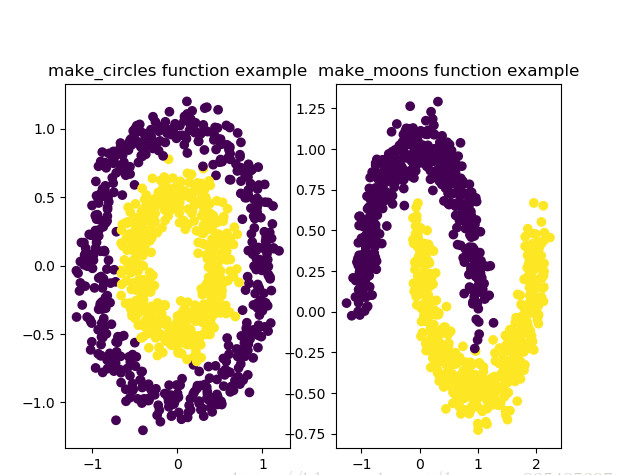
生成圆形数据
klearn.datasets.make_circles(n_samples=100, shuffle=True, noise=None, random_state=None, factor=0.8)
factor :外圈与内圈的尺度因子<1
生成半环形数据
sklearn.datasets.make_moons(n_samples=100, shuffle=True, noise=None, random_state=None)
from sklearn.datasets import make_circles from sklearn.datasets import make_moons import matplotlib.pyplot as plt fig = plt.figure(1) x1, y1 = make_circles(n_samples=1000, factor=0.5, noise=0.1) plt.subplot(121) plt.title('make_circles function example') plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1) plt.subplot(122) x1, y1 = make_moons(n_samples=1000, noise=0.1) plt.title('make_moons function example') plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1) plt.show()
参考:https://blog.csdn.net/luanpeng825485697/article/details/79808669



