python实现感知机

什么是感知机？

感知机是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型。

感知机的定义？

其图像表示为：

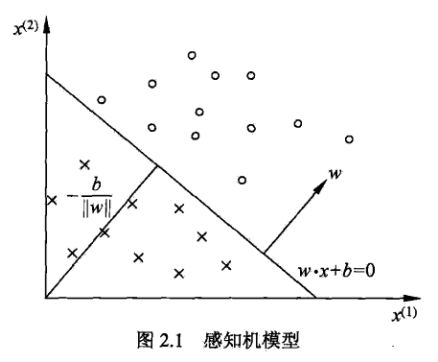
即找到分离超平面将不同类别的数据区分开来。

感知机的线性可分性？

感知机的损失函数？

感知机学习算法的原始形式？

举个例子：

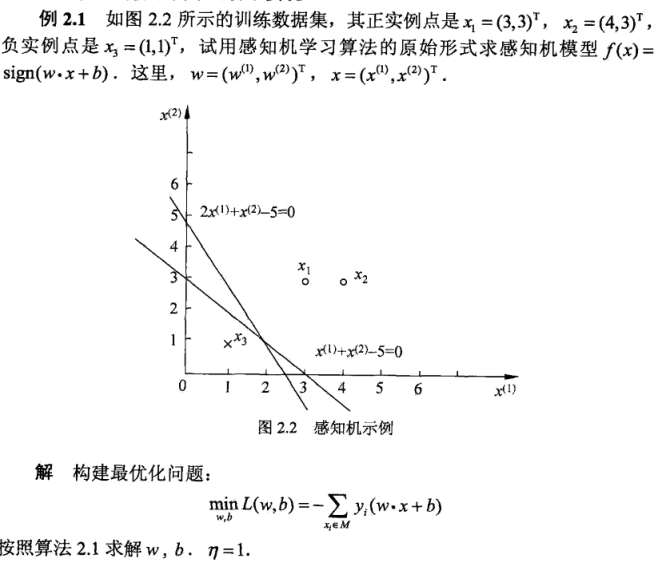
感知机学习的对偶形式？

 举个例子：

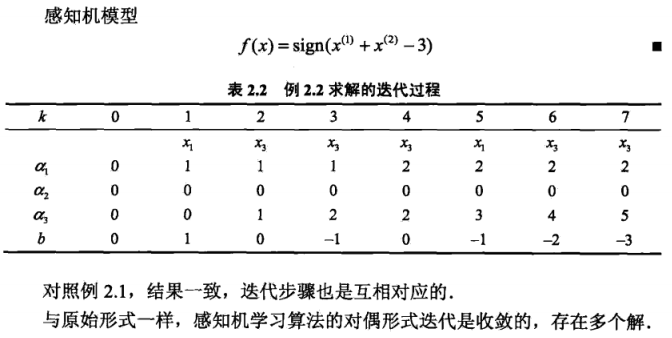
上述解释摘自《统计学习方法》 。

下面是代码实现：代码来源：https://github.com/eriklindernoren/ML-From-Scratch 

from __future__ import print_function, division
import math
import numpy as np

# Import helper functions
from mlfromscratch.utils import train_test_split, to_categorical, normalize, accuracy_score
from mlfromscratch.deep_learning.activation_functions import Sigmoid, ReLU, SoftPlus, LeakyReLU, TanH, ELU
from mlfromscratch.deep_learning.loss_functions import CrossEntropy, SquareLoss
from mlfromscratch.utils import Plot
from mlfromscratch.utils.misc import bar_widgets
import progressbar

class Perceptron():
    """The Perceptron. One layer neural network classifier.

    Parameters:
    -----------
    n_iterations: float
        The number of training iterations the algorithm will tune the weights for.
    activation_function: class
        The activation that shall be used for each neuron.
        Possible choices: Sigmoid, ExpLU, ReLU, LeakyReLU, SoftPlus, TanH
    loss: class
        The loss function used to assess the model's performance.
        Possible choices: SquareLoss, CrossEntropy
    learning_rate: float
        The step length that will be used when updating the weights.
    """
    def __init__(self, n_iterations=20000, activation_function=Sigmoid, loss=SquareLoss, learning_rate=0.01):
        self.n_iterations = n_iterations
        self.learning_rate = learning_rate
        self.loss = loss()
        self.activation_func = activation_function()
        self.progressbar = progressbar.ProgressBar(widgets=bar_widgets)

    def fit(self, X, y):
        n_samples, n_features = np.shape(X)
        _, n_outputs = np.shape(y)

        # Initialize weights between [-1/sqrt(N), 1/sqrt(N)]
        limit = 1 / math.sqrt(n_features)
        self.W = np.random.uniform(-limit, limit, (n_features, n_outputs))
        self.w0 = np.zeros((1, n_outputs))

        for i in self.progressbar(range(self.n_iterations)):
            # Calculate outputs
            linear_output = X.dot(self.W) + self.w0
            y_pred = self.activation_func(linear_output)
            # Calculate the loss gradient w.r.t the input of the activation function
            error_gradient = self.loss.gradient(y, y_pred) * self.activation_func.gradient(linear_output)
            # Calculate the gradient of the loss with respect to each weight
            grad_wrt_w = X.T.dot(error_gradient)
            grad_wrt_w0 = np.sum(error_gradient, axis=0, keepdims=True)
            # Update weights
            self.W  -= self.learning_rate * grad_wrt_w
            self.w0 -= self.learning_rate  * grad_wrt_w0

    # Use the trained model to predict labels of X
    def predict(self, X):
        y_pred = self.activation_func(X.dot(self.W) + self.w0)
        return y_pred

运行主代码：

from __future__ import print_function
from sklearn import datasets
import numpy as np

# Import helper functions
import sys
sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/")
from mlfromscratch.utils import train_test_split, normalize, to_categorical, accuracy_score
from mlfromscratch.deep_learning.activation_functions import Sigmoid
from mlfromscratch.deep_learning.loss_functions import CrossEntropy 
from mlfromscratch.utils import Plot
from mlfromscratch.supervised_learning import Perceptron


def main():
    data = datasets.load_digits()
    X = normalize(data.data)
    y = data.target

    # One-hot encoding of nominal y-values
    y = to_categorical(y)

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, seed=1)

    # Perceptron
    clf = Perceptron(n_iterations=5000,
        learning_rate=0.001, 
        loss=CrossEntropy,
        activation_function=Sigmoid)
    clf.fit(X_train, y_train)

    y_pred = np.argmax(clf.predict(X_test), axis=1)
    y_test = np.argmax(y_test, axis=1)

    accuracy = accuracy_score(y_test, y_pred)

    print ("Accuracy:", accuracy)

    # Reduce dimension to two using PCA and plot the results
    Plot().plot_in_2d(X_test, y_pred, title="Perceptron", accuracy=accuracy, legend_labels=np.unique(y))


if __name__ == "__main__":
    main()

其中相关函数如下：

def normalize(X, axis=-1, order=2):
    """ Normalize the dataset X """
    l2 = np.atleast_1d(np.linalg.norm(X, order, axis))
    l2[l2 == 0] = 1
    return X / np.expand_dims(l2, axis)

def train_test_split(X, y, test_size=0.5, shuffle=True, seed=None):
    """ Split the data into train and test sets """
    if shuffle:
        X, y = shuffle_data(X, y, seed)
    # Split the training data from test data in the ratio specified in
    # test_size
    split_i = len(y) - int(len(y) // (1 / test_size))
    X_train, X_test = X[:split_i], X[split_i:]
    y_train, y_test = y[:split_i], y[split_i:]

    return X_train, X_test, y_train, y_test

def shuffle_data(X, y, seed=None):
    """ Random shuffle of the samples in X and y """
    if seed:
        np.random.seed(seed)
    idx = np.arange(X.shape[0])
    np.random.shuffle(idx)
    return X[idx], y[idx]

class Sigmoid():
    def __call__(self, x):
        return 1 / (1 + np.exp(-x))

    def gradient(self, x):
        return self.__call__(x) * (1 - self.__call__(x))

class CrossEntropy(Loss):
    def __init__(self): pass

    def loss(self, y, p):
        # Avoid division by zero
        p = np.clip(p, 1e-15, 1 - 1e-15)
        return - y * np.log(p) - (1 - y) * np.log(1 - p)

    def acc(self, y, p):
        return accuracy_score(np.argmax(y, axis=1), np.argmax(p, axis=1))

    def gradient(self, y, p):
        # Avoid division by zero
        p = np.clip(p, 1e-15, 1 - 1e-15)
        return - (y / p) + (1 - y) / (1 - p)

运行结果：

Training: 100% [------------------------------------------------] Time: 0:00:09 Accuracy: 0.9527824620573356