python实现朴素贝叶斯

什么是朴素贝叶斯？

朴素贝叶斯是jiyu贝叶斯定理和特征条件独立假设的分类方法。即对于给定训练数据集，首先基于特征条件独立假设学习输入\输出的联合概率分布，然后基于此模型，对于给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

什么是贝叶斯法则？

在贝叶斯法则中，每个名词都有约定俗成的名称：
Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。
按这些术语，Bayes法则可表述为：
后验概率 = (似然度 * 先验概率)/标准化常量　也就是说，后验概率与先验概率和似然度的乘积成正比。
另外，比例Pr(B|A)/Pr(B)也有时被称作标准似然度（standardised likelihood），Bayes法则可表述为：
后验概率 = 标准似然度 * 先验概率。 

什么是条件独立性假设？

也就是Z事件发生时，X事件是否发生与Y无关，Y事件是否发生与X事件无关。

什么是联合概率分布？

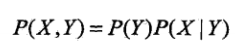
如何由联合概率模型得到朴素贝叶斯 模型？

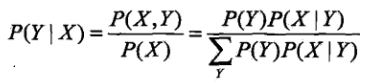
朴素贝叶斯参数估计：极大似然估计

朴素贝叶斯算法描述：

具体例子：

极大似然估计存在的问题？

使用贝叶斯估计求解上述问题？

朴素贝叶斯优缺点？

优点：
    （1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
    （2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
    （3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。
缺点：
    （1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
    （2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
    （3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
    （4）对输入数据的表达形式很敏感。

代码实现：

from __future__ import division, print_function
import numpy as np
import math
from mlfromscratch.utils import train_test_split, normalize
from mlfromscratch.utils import Plot, accuracy_score

class NaiveBayes():
    """The Gaussian Naive Bayes classifier. """
    def fit(self, X, y):
        self.X, self.y = X, y
        self.classes = np.unique(y)
        self.parameters = []
        # Calculate the mean and variance of each feature for each class
        for i, c in enumerate(self.classes):
            # Only select the rows where the label equals the given class
            X_where_c = X[np.where(y == c)]
            self.parameters.append([])
            # Add the mean and variance for each feature (column)
            for col in X_where_c.T:
                parameters = {"mean": col.mean(), "var": col.var()}
                self.parameters[i].append(parameters)

    def _calculate_likelihood(self, mean, var, x):
        """ Gaussian likelihood of the data x given mean and var """
        eps = 1e-4 # Added in denominator to prevent division by zero
        coeff = 1.0 / math.sqrt(2.0 * math.pi * var + eps)
        exponent = math.exp(-(math.pow(x - mean, 2) / (2 * var + eps)))
        return coeff * exponent

    def _calculate_prior(self, c):
        """ Calculate the prior of class c
        (samples where class == c / total number of samples)"""
        frequency = np.mean(self.y == c)
        return frequency

    def _classify(self, sample):
        """ Classification using Bayes Rule P(Y|X) = P(X|Y)*P(Y)/P(X),
            or Posterior = Likelihood * Prior / Scaling Factor

        P(Y|X) - The posterior is the probability that sample x is of class y given the
                 feature values of x being distributed according to distribution of y and the prior.
        P(X|Y) - Likelihood of data X given class distribution Y.
                 Gaussian distribution (given by _calculate_likelihood)
        P(Y)   - Prior (given by _calculate_prior)
        P(X)   - Scales the posterior to make it a proper probability distribution.
                 This term is ignored in this implementation since it doesn't affect
                 which class distribution the sample is most likely to belong to.

        Classifies the sample as the class that results in the largest P(Y|X) (posterior)
        """
        posteriors = []
        # Go through list of classes
        for i, c in enumerate(self.classes):
            # Initialize posterior as prior
            posterior = self._calculate_prior(c)
            # Naive assumption (independence):
            # P(x1,x2,x3|Y) = P(x1|Y)*P(x2|Y)*P(x3|Y)
            # Posterior is product of prior and likelihoods (ignoring scaling factor)
            for feature_value, params in zip(sample, self.parameters[i]):
                # Likelihood of feature value given distribution of feature values given y
                likelihood = self._calculate_likelihood(params["mean"], params["var"], feature_value)
                posterior *= likelihood
            posteriors.append(posterior)
        # Return the class with the largest posterior probability
        return self.classes[np.argmax(posteriors)]

    def predict(self, X):
        """ Predict the class labels of the samples in X """
        y_pred = [self._classify(sample) for sample in X]
        return y_pred

这里实现的是高斯贝叶斯估计，具体原理可参考：https://zhuanlan.zhihu.com/p/64498790

接着是主运行：

from __future__ import division, print_function
from sklearn import datasets
import numpy as np
import sys
sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/")
from mlfromscratch.utils import train_test_split, normalize, accuracy_score, Plot
from mlfromscratch.supervised_learning import NaiveBayes

def main():
    data = datasets.load_digits()
    X = normalize(data.data)
    y = data.target

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

    clf = NaiveBayes()
    clf.fit(X_train, y_train)
    y_pred = clf.predict(X_test)

    accuracy = accuracy_score(y_test, y_pred)

    print ("Accuracy:", accuracy)

    # Reduce dimension to two using PCA and plot the results
    Plot().plot_in_2d(X_test, y_pred, title="Naive Bayes", accuracy=accuracy, legend_labels=data.target_names)

if __name__ == "__main__":
    main()

运行结果：

Accuracy: 0.9122562674094707

 

 

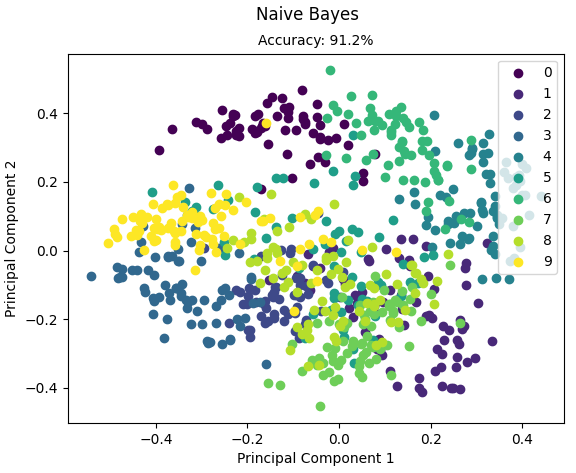
代码来源：https://github.com/eriklindernoren/ML-From-Scratch 

参考：

百度百科

https://blog.csdn.net/qiu_zhi_liao/article/details/90671932 

统计学习方法