python实现支持向量机之求解线性支持向量机（理论二）

上节讲到了支持向量机转换为以下问题了：

在线性可分的情况下，将距离分离超平面最近的样本点的实例称为支持向量，支持向量是使yi(wxi+b) -1=0的点。对于yi=+1的正例点，支持向量在超平面wx+b=1上，对于yi=-1的负例点，支持向量在wx+b=-1上，如图所示：

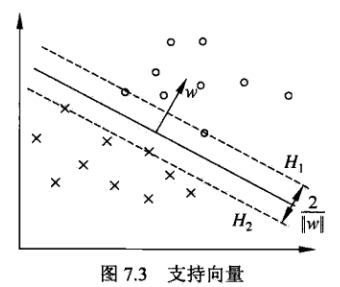
举个例子：

使用对偶算法求解支持向量机的好处：

1、对偶问题更易于求解

2、自然引入核函数，进而推广到非线性分类问题

如何利用对偶算法来求解？

首先建立拉格朗日函数：

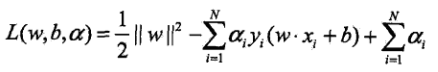
其中αi>=0，i=1,2,...,N。根据拉个朗日对偶性，原始问题的对偶问题是极大极小问题：

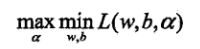
为了求得对偶问题的解，需要先求L(w,b,α)对w,b的极小，再求对α的极大。

所以，支持向量机就可以转换为以下问题了：

举个计算的例子：

以上摘自统计学习方法，仅为自己方便复习所用。