【python实现卷积神经网络】优化器的实现（SGD、Nesterov、Adagrad、Adadelta、RMSprop、Adam）
代码来源：https://github.com/eriklindernoren/ML-From-Scratch
卷积神经网络中卷积层Conv2D（带stride、padding）的具体实现：https://www.cnblogs.com/xiximayou/p/12706576.html
激活函数的实现（sigmoid、softmax、tanh、relu、leakyrelu、elu、selu、softplus）：https://www.cnblogs.com/xiximayou/p/12713081.html
损失函数定义（均方误差、交叉熵损失）：https://www.cnblogs.com/xiximayou/p/12713198.html
先看下优化器实现的代码：
import numpy as np from mlfromscratch.utils import make_diagonal, normalize # Optimizers for models that use gradient based methods for finding the # weights that minimizes the loss. # A great resource for understanding these methods: # http://sebastianruder.com/optimizing-gradient-descent/index.html class StochasticGradientDescent(): def __init__(self, learning_rate=0.01, momentum=0): self.learning_rate = learning_rate self.momentum = momentum self.w_updt = None def update(self, w, grad_wrt_w): # If not initialized if self.w_updt is None: self.w_updt = np.zeros(np.shape(w)) # Use momentum if set self.w_updt = self.momentum * self.w_updt + (1 - self.momentum) * grad_wrt_w # Move against the gradient to minimize loss return w - self.learning_rate * self.w_updt class NesterovAcceleratedGradient(): def __init__(self, learning_rate=0.001, momentum=0.4): self.learning_rate = learning_rate self.momentum = momentum self.w_updt = np.array([]) def update(self, w, grad_func): # Calculate the gradient of the loss a bit further down the slope from w approx_future_grad = np.clip(grad_func(w - self.momentum * self.w_updt), -1, 1) # Initialize on first update if not self.w_updt.any(): self.w_updt = np.zeros(np.shape(w)) self.w_updt = self.momentum * self.w_updt + self.learning_rate * approx_future_grad # Move against the gradient to minimize loss return w - self.w_updt class Adagrad(): def __init__(self, learning_rate=0.01): self.learning_rate = learning_rate self.G = None # Sum of squares of the gradients self.eps = 1e-8 def update(self, w, grad_wrt_w): # If not initialized if self.G is None: self.G = np.zeros(np.shape(w)) # Add the square of the gradient of the loss function at w self.G += np.power(grad_wrt_w, 2) # Adaptive gradient with higher learning rate for sparse data return w - self.learning_rate * grad_wrt_w / np.sqrt(self.G + self.eps) class Adadelta(): def __init__(self, rho=0.95, eps=1e-6): self.E_w_updt = None # Running average of squared parameter updates self.E_grad = None # Running average of the squared gradient of w self.w_updt = None # Parameter update self.eps = eps self.rho = rho def update(self, w, grad_wrt_w): # If not initialized if self.w_updt is None: self.w_updt = np.zeros(np.shape(w)) self.E_w_updt = np.zeros(np.shape(w)) self.E_grad = np.zeros(np.shape(grad_wrt_w)) # Update average of gradients at w self.E_grad = self.rho * self.E_grad + (1 - self.rho) * np.power(grad_wrt_w, 2) RMS_delta_w = np.sqrt(self.E_w_updt + self.eps) RMS_grad = np.sqrt(self.E_grad + self.eps) # Adaptive learning rate adaptive_lr = RMS_delta_w / RMS_grad # Calculate the update self.w_updt = adaptive_lr * grad_wrt_w # Update the running average of w updates self.E_w_updt = self.rho * self.E_w_updt + (1 - self.rho) * np.power(self.w_updt, 2) return w - self.w_updt class RMSprop(): def __init__(self, learning_rate=0.01, rho=0.9): self.learning_rate = learning_rate self.Eg = None # Running average of the square gradients at w self.eps = 1e-8 self.rho = rho def update(self, w, grad_wrt_w): # If not initialized if self.Eg is None: self.Eg = np.zeros(np.shape(grad_wrt_w)) self.Eg = self.rho * self.Eg + (1 - self.rho) * np.power(grad_wrt_w, 2) # Divide the learning rate for a weight by a running average of the magnitudes of recent # gradients for that weight return w - self.learning_rate * grad_wrt_w / np.sqrt(self.Eg + self.eps) class Adam(): def __init__(self, learning_rate=0.001, b1=0.9, b2=0.999): self.learning_rate = learning_rate self.eps = 1e-8 self.m = None self.v = None # Decay rates self.b1 = b1 self.b2 = b2 def update(self, w, grad_wrt_w): # If not initialized if self.m is None: self.m = np.zeros(np.shape(grad_wrt_w)) self.v = np.zeros(np.shape(grad_wrt_w)) self.m = self.b1 * self.m + (1 - self.b1) * grad_wrt_w self.v = self.b2 * self.v + (1 - self.b2) * np.power(grad_wrt_w, 2) m_hat = self.m / (1 - self.b1) v_hat = self.v / (1 - self.b2) self.w_updt = self.learning_rate * m_hat / (np.sqrt(v_hat) + self.eps) return w - self.w_updt
这里导入了了mlfromscratch.utils中的make_diagonal, normalize函数，它们在data_manipulation.py中。但是好像没有用到，还是去看一下这两个函数：
def make_diagonal(x): """ Converts a vector into an diagonal matrix """ m = np.zeros((len(x), len(x))) for i in range(len(m[0])): m[i, i] = x[i] return m
def normalize(X, axis=-1, order=2): """ Normalize the dataset X """ l2 = np.atleast_1d(np.linalg.norm(X, order, axis)) l2[l2 == 0] = 1 return X / np.expand_dims(l2, axis)
make_diagonal()的作用是将x中的元素变成对角元素。
normalize()函数的作用是正则化。
补充：
- np.linalg.norm(x, ord=None, axis=None, keepdims=False)：需要注意ord的值表示的是范数的类型。
- np.atleast_1d()：改变维度，将输入直接视为1维，比如np.atleast_1d([1])的输出就是[1]
- np.expand_dims()：用于扩展数组的维度，要深入了解还是得去查一下。
然后再看看优化器的实现，以最常用的随机梯度下降为例：
class StochasticGradientDescent(): def __init__(self, learning_rate=0.01, momentum=0): self.learning_rate = learning_rate self.momentum = momentum self.w_updt = None def update(self, w, grad_wrt_w): # If not initialized if self.w_updt is None: self.w_updt = np.zeros(np.shape(w)) # Use momentum if set self.w_updt = self.momentum * self.w_updt + (1 - self.momentum) * grad_wrt_w # Move against the gradient to minimize loss return w - self.learning_rate * self.w_updt
直接看带动量的随机梯度下降公式：
这里的β就是动量momentum的值，一般取值是0.9。正好是对应上面的公式，最后更新W和b就是：
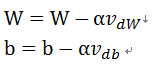
其中 α就表示学习率learning_rate。
至于不同优化器之间的优缺点就不在本文的考虑追之中了，可以自行去查下。
