洛谷 P3625 [APIO2009]采油区域

Description

原题链接

Solution

很巧妙的一种思想：分类讨论

分为 6 种情况，如下图：

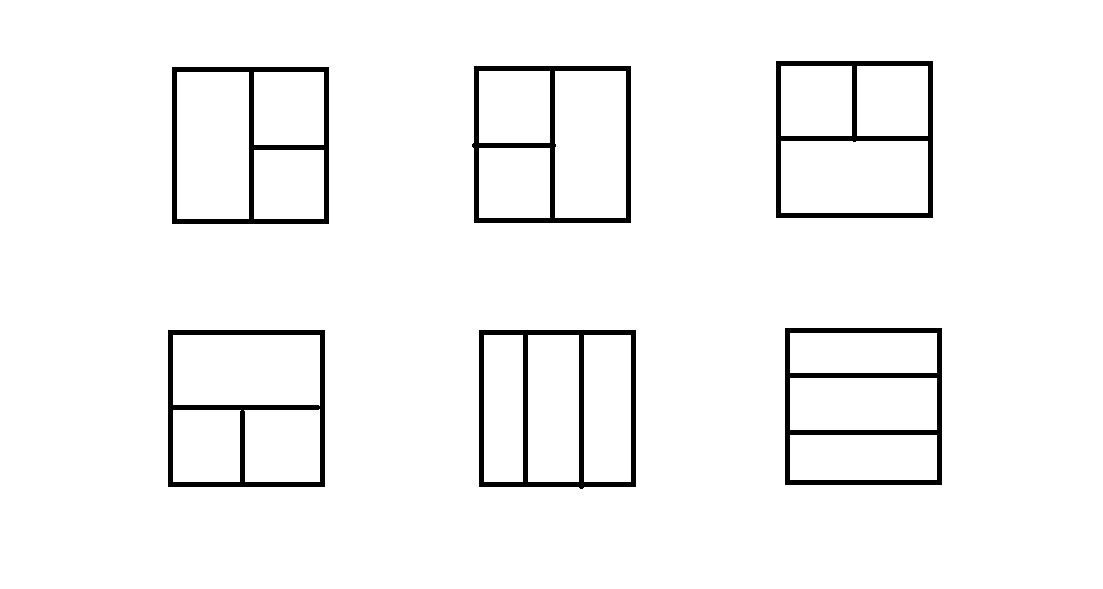
可以发现，每一张图都被分为了 3 块，我们就可以分别在这三个部分中各选择一个 \(k * k\) 的矩形，取最大值。

具体实现：

首先要进行预处理，设一个点为 \((x, y)\)

我们要预处理出以这个点为端点向左上，右上，左下，右下，四个方向分别的最大子矩阵。

然后我们枚举上图中每个矩形中的那两条线，再取最大值即可。

具体看代码吧。

Code

#include <iostream>
#include <cstdio>
#include <algorithm>
#define ri register int

using namespace std;

const int N = 1510;
int n, m, k, ans;
int sum[N][N], s[N][N], a[N][N], b[N][N], c[N][N], d[N][N];
//sum:前缀和  s: k * k区间和（详见下面） a,b,c,d: 四个方向，下面有图

inline int read(){
	int x = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
	return x;
}

/*
a  |  b 
———+————
c  |  d
*/

inline void init(){
	for(ri i = 1; i <= n; ++i)
		for(ri j = 1; j <= m; ++j)
			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + read();//二维前缀和
	for(ri i = k; i <= n; ++i)
		for(ri j = k; j <= m; ++j)
			s[i][j] = sum[i][j] - sum[i][j - k] - sum[i - k][j] + sum[i - k][j - k];//k * k区间和
//4 个方向预处理最大子矩阵
	for(ri i = k; i <= n; ++i)
		for(ri j = k; j <= m; ++j)
			a[i][j] = max(s[i][j], max(a[i][j - 1], a[i - 1][j]));
	for(ri i = k; i <= n; ++i)
		for(ri j = m - k + 1; j >= 1; j--)
			b[i][j] = max(s[i][j + k - 1], max(b[i - 1][j], b[i][j + 1]));
	for(ri i = n - k + 1; i >= 1; i--)
		for(ri j = k; j <= m; ++j)
			c[i][j] = max(s[i + k - 1][j], max(c[i + 1][j], c[i][j - 1]));
	for(ri i = n - k + 1; i >= 1; i--)
		for(ri j = m - k + 1; j >= 1; j--)
			d[i][j] = max(s[i + k - 1][j + k - 1], max(d[i + 1][j], d[i][j + 1]));
}

/*
a  |  b 
———+————
c  |  d
*/

inline void solve(){
	//两条竖线，两条横线的情况
	for(ri i = k; i <= n; ++i)
		for(ri j = k; j <= m; ++j){
			ans = max(ans, a[i - k][m] + s[i][j] + c[i + 1][m]);//两条横线
			ans = max(ans, a[n][j - k] + s[i][j] + b[n][j + 1]);//两条竖线
		}
	//剩下 4 种情况
	for(ri i = 1; i <= n; ++i)
		for(ri j = 1; j <= m; ++j){
			ans = max(ans, a[i][j] + b[i][j + 1] + c[i + 1][m]);
			ans = max(ans, a[i][m] + c[i][j] + d[i + 1][j + 1]);
			ans = max(ans, a[i][j] + b[n][j + 1] + c[i + 1][j]);
			ans = max(ans, a[n][j] + b[i][j + 1] + d[i + 1][j + 1]);
		}
}

signed main(){
	n = read(), m = read(), k = read();
	init();
	solve();
	printf("%lld\n", ans);
	return 0;
}

End