leetcode刷题记录——数组与矩阵
@
283. 移动零
开始的想法是把零都挪到后面,看到了一种效率更高的写法,思路是先遍历一遍数组,把遇到的非零数按顺序重新复制,后面的全修改成零
public void moveZeroes(int[] nums) {
int idx = 0;
for (int num : nums) {
if (num != 0) {
nums[idx++] = num;
}
}
while (idx < nums.length) {
nums[idx++] = 0;
}
}
566. 重塑矩阵
遍历
class Solution {
public int[][] matrixReshape(int[][] nums, int r, int c) {
int m = nums.length, n = nums[0].length;
if (m * n != r * c) {
return nums;
}
int[][] reshapedNums = new int[r][c];
int index = 0;
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
reshapedNums[i][j] = nums[index / n][index % n];
index++;
}
}
return reshapedNums;
}
}
485. 最大连续1的个数
双指针法
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int front = 0;
int last = 0;
int res = 0;
while (last < nums.length) {
if (nums[last] == 1) {
last ++;
}
/** 若出现0 保存当前最大连续值 重置指针*/
else {
res = Math.max(res, last - front);
front = last + 1;
last = front;
}
}
/** 判断最后的连续值是否是最大值 */
res = Math.max(res, last - front);
return res;
}
}
240. 搜索二维矩阵 II
因为每一行递增,每一列递增。
所以本题的思路是从右上角往左下角找或者从左下角往右上角找。每次比较可以排除一行或者一列,时间复杂度为O(m+n)
和之前剑指offer上的一个题差不多
https://blog.csdn.net/hide_on_rush/article/details/105165885
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return false;
int m = matrix.length, n = matrix[0].length;
int row = 0, col = n - 1;
while (row < m && col >= 0) {
if (target == matrix[row][col]) return true;
else if (target < matrix[row][col]) col--;
else row++;
}
return false;
}
}
378. 有序矩阵中第K小的元素
二分查找法
public int kthSmallest(int[][] matrix, int k) {
int m = matrix.length, n = matrix[0].length;
int lo = matrix[0][0], hi = matrix[m - 1][n - 1];
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
int cnt = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n && matrix[i][j] <= mid; j++) {
cnt++;
}
}
if (cnt < k) lo = mid + 1;
else hi = mid - 1;
}
return lo;
}
645. 错误的集合
开始的想法是先排序,这种方法时间复杂度为 O(NlogN)。但是可以通过交换数组元素,使得数组上的元素在正确的位置上。这样的话时间复杂度为O(N),
空间复杂度为O(1)。
class Solution {
public int[] findErrorNums(int[] nums) {
for (int i = 0; i < nums.length; i++) {
while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i]) {
swap(nums, i, nums[i] - 1);
}
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] != i + 1) {
return new int[]{nums[i], i + 1};
}
}
return null;
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
287. 寻找重复数
双指针解法要比二分法效率高
题解里找到的思路:
这里一共有n+1个元素,且元素的值为 [ 1 , n ],因此这里把下标i当做结点的标志,nums[ i ]当做是结点i的下一个结点的标志。这样从结点1到结点n中的任一个结点开始跳,必然会出现两种情况:
1.形成局部环(循环起始点不是初始点)
2.形成全局环(循环起始点是初始点)
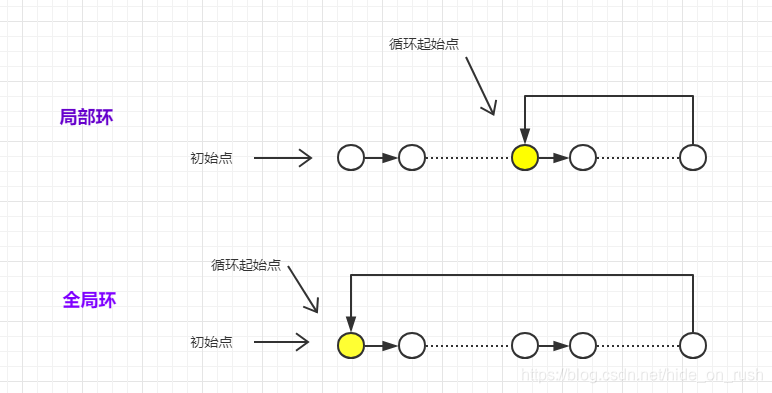
情况1:如果是局部环,那么循环起始点的标志就是重复数字。
情况2:如果是全局环,则稍微复杂一点,因为它只能说明环内的结点所对应的值不重复,但整个全局环不一定包含所有结点。为了判断是否含有重复,还需要从剩下的点继续跳。
解决办法:由于情况2比较难处理(因为要判断剩余的结点是哪些),因此这里有一个小小的tips,我们不再是从结点1到结点n中任意位置起跳,而是从结点nums[ 0 ]起跳,这样即使形成的是全局环,循环的起点依然是重复数字(因为全局环意味着环内的末节点指向初始结点,而结点0又指向初始结点,因此,初始结点即循环起始点就是重复数字)。这样,无论情况1还是情况2,我们只需要找到循环起始点就可以了。
作者:shi-wen
链接:https://leetcode-cn.com/problems/find-the-duplicate-number/solution/kuai-man-zhi-zhen-de-yuan-li-0ms-100-by-shi-wen/
public int findDuplicate(int[] nums) {
int slow = nums[0], fast = nums[nums[0]];
while (slow != fast) {
slow = nums[slow];
fast = nums[nums[fast]];
}
fast = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
667. 优美的排列 II
class Solution {
public int[] constructArray(int n, int k) {
int[] ret = new int[n];
ret[0] = 1;
for (int i = 1, interval = k; i <= k; i++, interval--) {
ret[i] = i % 2 == 1 ? ret[i - 1] + interval : ret[i - 1] - interval;
}
for (int i = k + 1; i < n; i++) {
ret[i] = i + 1;
}
return ret;
}
}
697. 数组的度
使用HashMap
class Solution {
public int findShortestSubArray(int[] nums) {
Map<Integer, Integer> numsCnt = new HashMap<>();
Map<Integer, Integer> numsLastIndex = new HashMap<>();
Map<Integer, Integer> numsFirstIndex = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
numsCnt.put(num, numsCnt.getOrDefault(num, 0) + 1);
numsLastIndex.put(num, i);
if (!numsFirstIndex.containsKey(num)) {
numsFirstIndex.put(num, i);
}
}
int maxCnt = 0;
for (int num : nums) {
maxCnt = Math.max(maxCnt, numsCnt.get(num));
}
int ret = nums.length;
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
int cnt = numsCnt.get(num);
if (cnt != maxCnt) continue;
ret = Math.min(ret, numsLastIndex.get(num) - numsFirstIndex.get(num) + 1);
}
return ret;
}
}
766. 托普利茨矩阵
每个元素都跟左上角元素比较,因为第0行和第0列都没有左上角元素,所以两个索引都从1开始。
class Solution {
public boolean isToeplitzMatrix(int[][] matrix) {
for(int i = 1; i < matrix.length; i ++)
for(int j = 1; j < matrix[0].length; j ++)
if(matrix[i][j] != matrix[i-1][j-1])
return false;
return true;
}
}
565. 数组嵌套
将访问过的数标位-1,访问到-1直接跳出。原理是如果访问到之前一个循环中访问过的数,则说明也进入了之前的循环,没有必要再进行下去。
class Solution {
public int arrayNesting(int[] nums) {
int res = 0;
for(int i = 0; i < nums.length; i++){
int count = 0;
int k = i;
while(nums[k]!=-1){
int temp = k;
k = nums[k];
nums[temp] = -1;
count++;
}
res = Math.max(res,count);
}
return res;
}
}
769. 最多能完成排序的块
class Solution {
public int maxChunksToSorted(int[] arr) {
if (arr == null) return 0;
int ret = 0;
int right = arr[0];
for (int i = 0; i < arr.length; i++) {
right = Math.max(right, arr[i]);
if (right == i) ret++;
}
return ret;
}
}


