HDU - 6395 Sequence (分块+快速矩阵幂)

给定递推式：

　　

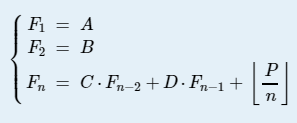
求Fn.

分析：给出的公式可以用快速矩阵幂运算得到，但 P/n 整除对于不同的i，值是不同的。

可以根据P将3-n分成若干块，每块中P整除n的值是相同的。分块的时候要注意判断。

将每块的快速幂结果累乘得到结果。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int MAXN = 1e5+10;
const int SIZE = 3;
const int MOD = 1e9+7;
int N;
int A, B, C, D, P;
int cc;

LL ret_multi[SIZE][SIZE];
void multi(LL a[][SIZE], LL b[][SIZE])
{
    memset(ret_multi, 0, sizeof ret_multi);
    for( int i = 0; i < SIZE; i++ )
        for( int j = 0; j < SIZE; j++)
            for( int k = 0; k < SIZE; k++ )
                ret_multi[i][j] = (ret_multi[i][j] + a[i][k] *b[k][j]) %MOD;
    for( int i = 0; i < SIZE; i++ )
        for( int j = 0; j < SIZE; j++)
            a[i][j] = ret_multi[i][j];
}

LL ret_qpow[SIZE][SIZE];
LL base[SIZE][SIZE];
void qpow(LL b[][SIZE], LL index)
{
    memset(ret_qpow, 0, sizeof ret_qpow);
    memcpy(base, b, sizeof base);

    for( int i = 0; i < SIZE; i++) ret_qpow[i][i] = 1;
    while(index){
        if( index &1)
            multi(ret_qpow, base);
        index /= 2;
        multi(base, base);
    }
}

LL m[][SIZE] = {
    {D, C, cc},
    {1, 0, 0},
    {0, 0, 1}
};

LL f[][SIZE] = {
    {B, 0, 0},
    {A, 0, 0},
    {1, 0, 0}
};

int getRight(int cc)
{
    int L = 1, R = N;
    int ret = N;
    while(L <= R){
        int mid = L + (R-L)/2;
        if( P/mid >= cc){
            ret = mid;
            L = mid+1;
        }
        else R = mid-1;
    }
    return ret;
}

vector<PII> range;

int main()
{
    #ifndef ONLINE_JUDGE
            freopen("in.txt","r",stdin);
            freopen("out.txt","w",stdout);
    #endif

    int T;  scanf("%d",&T);
    while(T--){
        range.clear();
        scanf("%d%d%d%d%d%d",&A,&B,&C,&D,&P,&N);
        if(N==1){
            printf("%d\n",A); continue;
        }
        else if(N==2){
            printf("%d\n",&B); continue;
        }
        for( int i = 3; i <= N; i++ )       //分块
        {
            int cc = P/i;
            int j = getRight(cc);
            range.push_back({i, j});
            i = j;
        }

        LL m[][SIZE] = {
            {D, C, cc},
            {1, 0, 0},
            {0, 0, 1}
        };

        LL f[][SIZE] = {
            {B, 0, 0},
            {A, 0, 0},
            {1, 0, 0}
        };

        for( PII rng :range){
            const int &n1 = rng.first;
            const int &n2 = rng.second;
            cc = P/n1;

            m[0][2] = cc;

            qpow(m, n2-(n1-1));
            multi(ret_qpow, f);

            memcpy(f, ret_multi, sizeof f);
        }
        printf("%lld\n",f[0][0]%MOD);
    }
    return 0;
}