uva 11426 GCD - Extreme (II) (欧拉函数打表)

题意：给一个N，和公式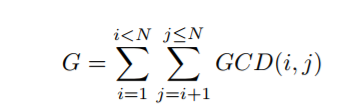

求G(N)。

分析：设F(N)= gcd(1,N)+gcd(2,N)+...gcd(N-1,N)。则 G(N ) = G(N-1) + F(N)。

设满足gcd(x,N) 值为 i 的且1<=x<=N-1的x的个数为 g(i,N)。 则F(N)  = sigma{ i * g(i,N) }。

因为gcd(x,N) == i 等价于 gcd(x/i, N/i)  == 1，且满足gcd(x/i , N/i)==1的x的个数就是 N/i 的欧拉函数值。所以g(i,N) 的值 就是phi(N/i)。

打表预处理出每个数的欧拉函数值和每个数对应的答案即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 4e6+5;
int phi[maxn];              //欧拉函数
LL ans[maxn];
void Euler()
{             //欧拉函数表
    for(int i=1;i<maxn;++i) phi[i] = i;
    for(int i=2;i<maxn;++i){
        if(phi[i]!=i) continue;
        for(int j=i;j<maxn;j+=i)
            phi[j] = phi[j] - phi[j]/ i;
    }
    for(int i=1;i<maxn;++i){
        for(int j=i+i;j<maxn;j+=i){
            ans[j] += i*phi[j/i];
        }
    }
    for(int i=2;i<maxn;++i) ans[i]+=ans[i-1];
}

int main() 
{
    #ifndef ONLINE_JUDGE
            freopen("in.txt","r",stdin);
            freopen("out.txt","w",stdout);
    #endif
    Euler();
    int N;
    while(scanf("%d",&N)==1){
        if(!N) break;
        printf("%lld\n",ans[N]);
    }
    return 0;
}