算法——归并和归并排序

一、归并

　　假设现在的列表分两段有序，如何将其合成为一个有序列表。这种操作称为一次归并。

1、归并过程图示

　　当一个列表两段有序合并为一个有序列表的一次归并的过程如下：

　　将列表分为两段，两个箭头分别指向每段的第一个：

　　

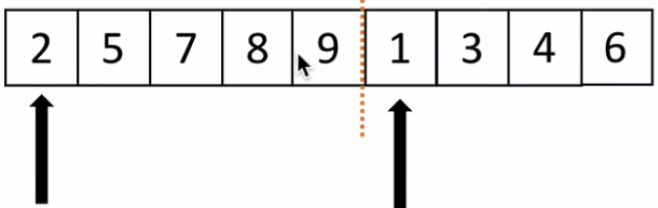
　　比较两段中最小的数2和1，将最小的那个值，箭头后移：

　　

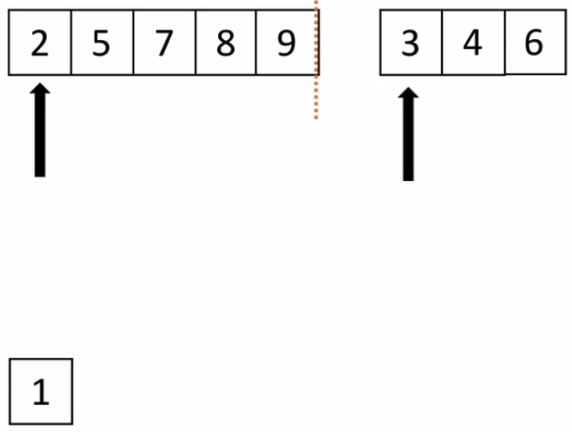
　　接着比较两段中最小的数，将2取出，箭头后移，以此类推：

　　

 

2、归并代码实现

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

def merge(li, low, mid, high):     """     归并过程     :param li:列表     :param low:第一段第一个元素     :param mid:第一段最后一个元素     :param high:第二段最后一个元素     :return:     """     i = low     j = mid + 1   # 第二段第一个元素     ltmp = []  # 新列表     while i <= mid and j<= high:    # 只要左右两边都有数         if li[i] < li[j]:             ltmp.append(li[i])             i += 1         else:             ltmp.append(li[j])             j += 1     # while执行完，肯定会有一部分没数了     while i<= mid :   # 如果是第一部分仍有数         ltmp.append(li[i])         i += 1     while j <= high:   # 如果是第二部分仍有数         ltmp.append(li[j])         j += 1     # 将ltmp的值写回到li     li[low:high+1] = ltmp   # 切片往回写     li = [2, 4, 5, 7, 1, 3, 6, 8] merge(li, 0, 3, 7) print(li) """ [1, 2, 3, 4, 5, 6, 7, 8] """

二、归并排序——使用归并

　　归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

1、归并排序图示

　　

　　分解：将列表越分越小，直至分成一个元素。

　　终止条件：一个元素是有序的。

　　合并：将两个有序列表归并，列表越来越大。

2、归并排序代码实现

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

def merge(li, low, mid, high):     """     归并过程     :param li:列表     :param low:第一段第一个元素     :param mid:第一段最后一个元素     :param high:第二段最后一个元素     :return:     """     i = low     j = mid + 1   # 第二段第一个元素     ltmp = []  # 新列表     while i <= mid and j<= high:    # 只要左右两边都有数         if li[i] < li[j]:             ltmp.append(li[i])             i += 1         else:             ltmp.append(li[j])             j += 1     # while执行完，肯定会有一部分没数了     while i<= mid :   # 如果是第一部分仍有数         ltmp.append(li[i])         i += 1     while j <= high:   # 如果是第二部分仍有数         ltmp.append(li[j])         j += 1     # 将ltmp的值写回到li     li[low:high+1] = ltmp   # 切片往回写     def _merge_sort(li, low, high):     # 递归函数     """归并排序"""     if low < high:    # 翟少有两个元素，递归         mid = (low + high) // 2         _merge_sort(li, low, mid)    # 把左边排好序         _merge_sort(li, mid+1, high)   # 把右边排好序         merge(li, low, mid, high)         print(li[low: high+1])     def merge_sort(li):     return _merge_sort(li, 0, len(li)-1)     li = list(range(10)) import random random.shuffle(li) print(li) merge_sort(li) print(li) """ [6, 2, 8, 3, 1, 9, 7, 5, 4, 0] [2, 6] [2, 6, 8] [1, 3] [1, 2, 3, 6, 8] [7, 9] [5, 7, 9] [0, 4] [0, 4, 5, 7, 9] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] """

3、归并和归并排序时间、空间复杂度　　

　　每一层的时间复杂度是O(n)，层数是logn。因此总的时间复杂度是O(nlogn)。

　　由于merge函数创建了一个ltmp的临时空间，到最大的时候长度是n，空间复杂度是O(n)。不再是原地排序。