算法——堆和堆排序介绍
一、什么是堆?
堆:一种特殊的完全二叉树结构。

大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大;
小根堆:一棵完全二叉树,满足任一节点都比其他孩子节点小。
二、堆的向下调整性质
假设:节点的左右子树都是堆,但自身不是堆。
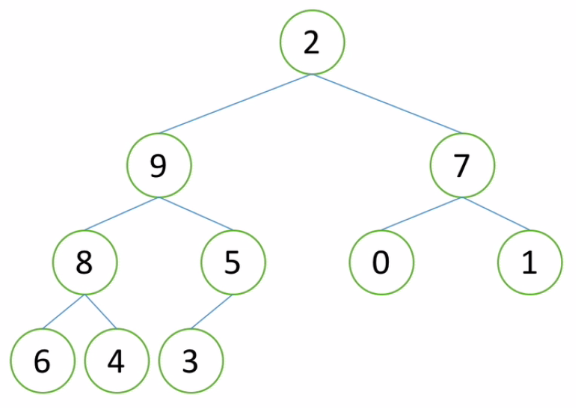
1、图示向下调整过程
由于左右子树都是大根堆,但是2并不比其孩子节点大,因此2不称职,需要更换新的领导

2也不够资格做8、5的父节点,继续下移,8提上来做父节点:
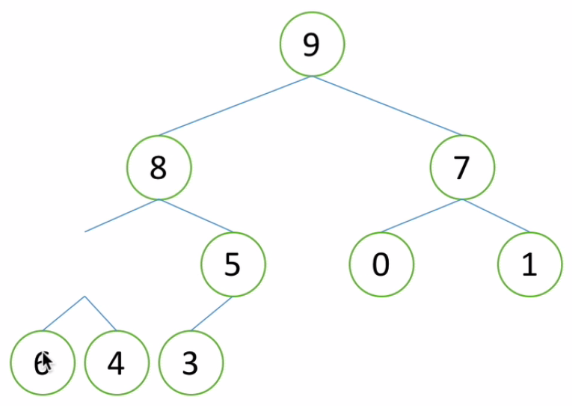
2也不够资格做6、4的父节点,将6提上来做父节点,2放到6原来的位置,成为叶子节点:

2、堆向下调整总结
当根节点的左右子树都是堆时(根节点不满足堆的性质),可以通过一次向下的调整来将其变换成一个堆。
三、堆排序
1、堆排序过程
1、建立堆
2、得到堆顶元素为最大元素
3、去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。
4、堆顶元素为第二大元素。
5、重复步骤3,知道堆变空
2、堆排序过程——挨个出数图示
(1)如下图所示为一个堆,9为堆顶元素,也是堆的最大元素

(2)去除堆顶元素9,将堆最后元素3放到堆顶

(3)此时满足了向下调整的条件,用向下调整以保证仍为一个堆(完全二叉树)

(4)此时堆顶元素8是第二大元素,再次去除堆顶元素8,再次将3提到堆顶。

(5)再次满足向下调整的条件,做向下调整,依此类推。

3、堆排序过程——构造堆图示
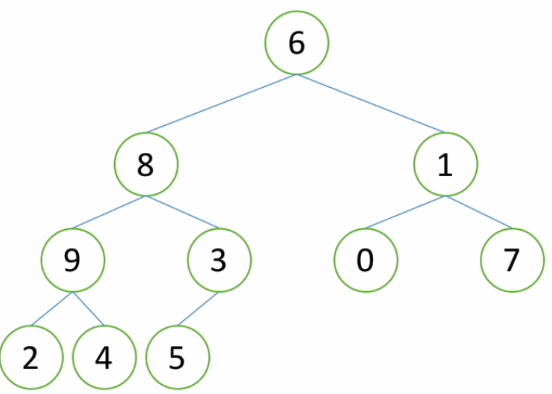
如上图所示的二叉树不符合堆的结构特征,由于向下调整的性质,构造堆首先要让下级先有序。
(1)如果有很多层怎么看?看最后一个非叶子节点!对子树做一次调整

(2)再看前一个非叶子节点,该子树符合堆的结构特点因此不做调整
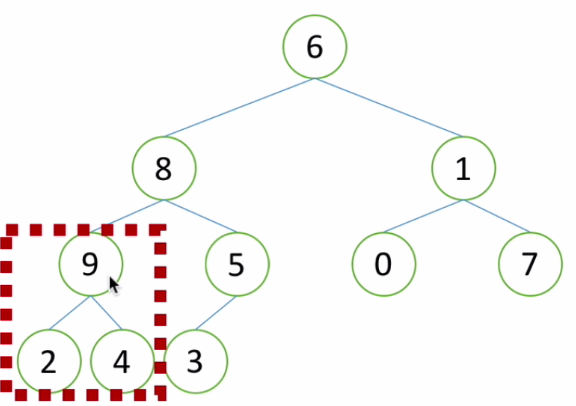
(3)再看前一个非叶子节点,该子树不符合堆结构,进行子树调整
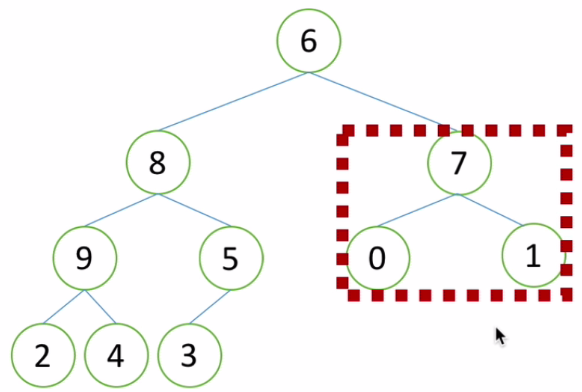
(4)再观察前一个非叶子节点,以整体作为子树调整

(5)到这一步之后就又开始了向下调整,堆也就构造完成了

四、堆排序代码实现

在实际实现中为了最大节省空间和时间,并不会重新生成一个空间存放堆顶元素。而是将堆顶元素(9)和最后一个元素(3)进行交换。并标记9这个元素不在堆内,只是占用了一个位置,标记元素(4)是堆的最后一个元素。
1、向下调整函数的实现
def sift(li, low, high):
"""
向下调整函数
:param li:列表
:param low:堆的根节点位置
:param high:堆的最后一个元素的位置
:return:
"""
i = low # 父节点位置(编号下标)最开始指向根节点(0)
j = 2 * i + 1 # 子节点位置(左孩子节点编号下标为2i+1)
tmp = li[low] # 把堆顶存起来
while j<= high: # 只要j位置有值就一直循环(保证不越界)
if j<= high and li[j+1] > li[j]: # 如果右孩子存在并且大于左孩子
j = j + 1 # 将j指向右孩子
if li[j] > tmp: # 如果下标j节点元素大于堆顶元素
li[i] = li[j] # 将j位置上的数写到i位置(空位置)上
i = j # 再往下看一层
j = 2 * i +1 # j指向下一层的左子孩子
else: # 如果tmp更大,将tmp放到i的位置上
li[i] = tmp # 循环跳出条件一:tmp放到了某一个父节点位置上
break
else: # 循环跳出条件二:j>high ,此时i已经指向了叶子节点,i不存在子节点了
li[i] = tmp # 将tmp放在叶子节点上
2、使用sift函数实现堆排序
def heap_sort(li):
n = len(li)
"""建堆"""
for i in range((n-2)//2, -1, -1): # i从n-2整除2开始倒着遍历到0,一个一个子树调整
# i表示建堆的时候调整的部分根的下标。
sift(li, i, n-1)
"""挨个出数"""
for i in range(n-1, -1, -1): # i从n-1开始一直到零
# i指向当前堆的最后一个元素
li[0], li[i] = li[i], li[0] # 堆顶(li[0])和最后一个元素(li[i])交换位置
sift(li, 0, i-1) # i-1是新的high,堆中最后一个元素
五、堆排序时间复杂度
首先sift函数最多是走一个树的高度层(走左边右边就不用考虑),因此它的时间复杂度是logn。
由此可见heap_sort是2个nlogn,因此堆排序的时间复杂度是nlogn级别。
六、python堆排序内置模块(heapq)
import heapq # q——》queue优先队列
import random
li = list(range(10))
random.shuffle(li)
print(li)
heapq.heapify(li) # 建堆
print(li)
n = len(li)
for i in range(n):
print(heapq.heappop(li), end=',') # 每次弹出最小元素
"""
[3, 4, 7, 6, 2, 5, 1, 0, 8, 9]
[0, 2, 1, 4, 3, 5, 7, 6, 8, 9]
0,1,2,3,4,5,6,7,8,9,
"""
七、topk问题(堆应用)
1、什么是topk问题?
现在有n个数,设计算法得到前k大的数。(k<n)
常用于实现网站热搜榜等。
2、解决思路
(1)排序后切片:O(nlogn)
(2)排序LowB三人组:O(kn)
(3)堆排序的思路:O(nlogk)
取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数(最小的数)。
依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且对堆进行依次调整。
遍历列表所有元素后,倒序弹出堆顶。
3、堆排序思路图解
比如要从以下这十个数中取前五大的数:

先取前五个数建立一个小根堆:

现在堆顶1就是小根堆中第五大的数,下一个数是0,比1还要小,直接排除。
再下一个数是7,7比1大,因此7把1换掉:

小根堆向下调整:

接着看2,2比3小,直接排除,4比3大替换3,5比4大替换4.均不需要做向下调整:
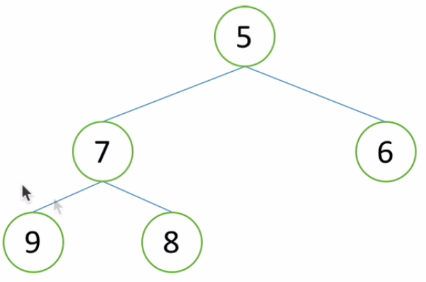
这样就得到了前5大的数。它还是需要遍历所有的数来判断每个数是否进堆(O(n)),同时堆的大小是k,因此调整的复杂度是O(logk)。所以总的时间复杂度是O(nlogk)
4、基于堆排序的topk代码实现
def sift(li, low, high):
"""
向下调整函数 (小根堆)
:param li:列表
:param low:堆的根节点位置
:param high:堆的最后一个元素的位置
:return:
"""
i = low # 父节点位置(编号下标)最开始指向根节点(0)
j = 2 * i + 1 # 子节点位置(左孩子节点编号下标为2i+1)
tmp = li[low] # 把堆顶存起来
while j<= high: # 只要j位置有值就一直循环(保证不越界)
# if j+1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且大于左孩子
if j + 1 <= high and li[j + 1] < li[j]: # 取两个孩子里小的那个
j = j + 1 # 将j指向右孩子
# if li[j] > tmp: # 如果下标j节点元素大于堆顶元素
if li[j] < tmp: # 只要小于省长就放过来,满足父亲比孩子小
li[i] = li[j] # 将j位置上的数写到i位置(空位置)上
i = j # 再往下看一层
j = 2 * i +1 # j指向下一层的左子孩子
else: # 如果tmp更大,将tmp放到i的位置上
li[i] = tmp # 循环跳出条件一:tmp放到了某一个父节点位置上
break
else: # 循环跳出条件二:j>high ,此时i已经指向了叶子节点,i不存在子节点了
li[i] = tmp # 将tmp放在叶子节点上
def topk(li, k):
heap = li[0:k]
for i in range((k-2)//2, -1, -1): # i从k-2整除2开始倒着遍历到-1
sift(heap, i, k-1)
# 1.建堆
for i in range(k, len(li)-1):
if li[i] > heap[0]:
heap[0] = li[i] # 用li[i]覆盖heap[0]的值
sift(heap, 0, k-1) # 将小根堆做一次调整
# 2.遍历heap
for i in range(k-1, -1, -1): # i从k-1开始一直到零
# i指向当前堆的最后一个元素
heap[0], heap[i] = heap[i], heap[0] # 堆顶(li[0])和最后一个元素(li[i])交换位置
sift(heap, 0, i-1) # i-1是新的high,堆中最后一个元素
# 3.出数
return heap
li = list(range(100))
import random
random.shuffle(li)
print(li)
print(topk(li, 5))
"""
[28, 82, 65, 98, 54, 47, 79, 46, 19, 85, 26, 52, 69, 97, 91, 36, 81, 58, 87, 50, 24, 3, 17, 35, 39, 94, 11, 90, 74, 48, 68, 8, 7, 77, 57, 6, 44, 40, 14, 86, 23, 30, 45, 89, 31, 96, 9, 93, 84, 20, 15, 22, 67, 34, 66, 71, 59, 73, 41, 92, 63, 55, 12, 10, 99, 21, 49, 2, 4, 29, 0, 70, 51, 32, 27, 64, 76, 38, 53, 56, 61, 5, 62, 13, 78, 25, 18, 88, 16, 60, 83, 72, 43, 33, 80, 75, 1, 37, 95, 42]
[99, 98, 97, 96, 95]
"""



 浙公网安备 33010602011771号
浙公网安备 33010602011771号