算法——列表排序和常用排序算法
一、列表排序
排序就是将一组“无序”的记录序列调整为“有序”的记录序列。
列表排序：将无序列表变为有序列表。
输入：列表
输出：有序列表
两种基本的排序方式：升序和降序。
python内置的排序函数：sort()。
二、常见排序算法
|
名称 |
复杂度 |
说明 |
备注 |
|
冒泡排序 |
O(N*N) |
将待排序的元素看作是竖着排列的“气泡”，较小的元素比较轻，从而要往上浮 |
|
|
插入排序 Insertion sort |
O(N*N) |
逐一取出元素，在已经排序的元素序列中从后向前扫描，放到适当的位置 |
起初，已经排序的元素序列为空 |
|
选择排序 |
O(N*N) |
首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾。以此递归。 |
|
|
快速排序 Quick Sort |
O(n *log2(n)) |
先选择中间值，然后把比它小的放在左边，大的放在右边（具体的实现是从两边找，找到一对后交换）。然后对两边分别使用这个过程（递归）。 |
|
|
堆排序HeapSort |
O(n *log2(n)) |
利用堆（heaps）这种数据结构来构造的一种排序算法。堆是一个近似完全二叉树结构，并同时满足堆属性：即子节点的键值或索引总是小于（或者大于）它的父节点。 |
近似完全二叉树 |
|
希尔排序 SHELL |
O(n1+￡) 0<￡<1 |
选择一个步长(Step) ,然后按间隔为步长的单元进行排序.递归,步长逐渐变小,直至为1. |
|
|
箱排序 |
O(n) |
设置若干个箱子，把关键字等于 k 的记录全都装入到第k 个箱子里 ( 分配 ) ，然后按序号依次将各非空的箱子首尾连接起来 ( 收集 ) 。 |
分配排序的一种：通过" 分配 " 和 " 收集 " 过程来实现排序。 |
1、冒泡排序（Bubble Sort）
列表每两个相邻的数，如果前面比后面大，则交换这两个数。
一趟排序完成后，则无序区减少一个数，有序区增加一个数。
代码关键点：趟、无序区范围。
（1）图示说明
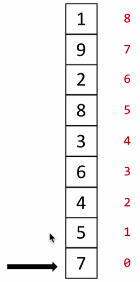
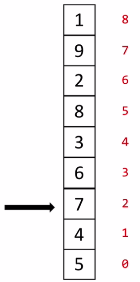
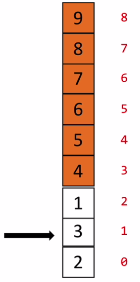
这样排序一趟后，最大的数9，就到了列表最顶成为了有序区，下面的部分则还是无序区。然后在无序区不断重复这个过程，每完成一趟排序，无序区减少一个数，有序区增加一个数。图示最后一张图要开始第六趟排序，排序从第0趟开始计数。剩一个数的时候不需要排序了，因此整个排序排了n-1趟。
（2）代码示例
import random
def bubble_sort(li):
for i in range(len(li)-1): # 总共是n-1趟
for j in range(len(li)-i-1): # 每一趟都有箭头，从0开始到n-i-1
if li[j] > li[j+1]: # 比对箭头指向和箭头后面的那个数的值
# 当箭头所指数大于后面的数时交换位置, 升序排列；条件相反则为降序排列
li[j], li[j+1] = li[j+1], li[j]
li = [random.randint(0, 10000) for i in range(30)]
print(li)
bubble_sort(li)
print(li)
"""
[5931, 5978, 6379, 4217, 9597, 4757, 4160, 3310, 6916, 2463, 9330, 8043, 8275, 5614, 8908, 7799, 9256, 3097, 9447, 9327, 7604, 9464, 417, 927, 1720, 145, 6451, 7050, 6762, 6608]
[145, 417, 927, 1720, 2463, 3097, 3310, 4160, 4217, 4757, 5614, 5931, 5978, 6379, 6451, 6608, 6762, 6916, 7050, 7604, 7799, 8043, 8275, 8908, 9256, 9327, 9330, 9447, 9464, 9597]
"""
如果要打印出每次排序结果：
import random
def bubble_sort(li):
for i in range(len(li)-1): # 总共是n-1趟
for j in range(len(li)-i-1): # 每一趟都有箭头，从0开始到n-i-1
if li[j] > li[j+1]: # 比对箭头指向和箭头后面的那个数的值
# 当箭头所指数大于后面的数时交换位置, 升序排列；条件相反则为降序排列
li[j], li[j+1] = li[j+1], li[j]
print(li)
li = [random.randint(0, 10000) for i in range(5)]
print(li)
bubble_sort(li)
print(li)
"""
[1806, 212, 4314, 1611, 8355]
[212, 1806, 1611, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
"""
（3）算法时间复杂度
n是列表的长度，算法中也没有发生循环折半的过程，具备两层关于n的循环，因此它的时间复杂度是O(n2)。
（4）冒泡排序优化
如果在一趟排序过程中没有发生交换就可以认定已经排好序了。因此可做如下优化：
import random
def bubble_sort(li):
for i in range(len(li)-1): # 总共是n-1趟
exchange = False
for j in range(len(li)-i-1): # 每一趟都有箭头，从0开始到n-i-1
if li[j] > li[j+1]: # 比对箭头指向和箭头后面的那个数的值
# 当箭头所指数大于后面的数时交换位置, 升序排列；条件相反则为降序排列
li[j], li[j+1] = li[j+1], li[j]
exchange = True # 如果发生了交换就置为true
print(li)
if not exchange:
# 如果exchange还是False，说明没有发生交换，结束代码
return
# li = [random.randint(0, 10000) for i in range(5)]
li = [1806, 212, 4314, 1611, 8355]
bubble_sort(li)
"""
[212, 1806, 1611, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
[212, 1611, 1806, 4314, 8355]
"""
对比前面排序的次数少了很多，算法得到了优化~
2、选择排序（Selection Sort）
一趟遍历完记录最小的数，放到第一个位置；再一趟遍历记录剩余列表中的最小的数，继续放置。
算法关键点：有序区和无序区、无序区最小数的位置。
（1）简单的选择排序
def select_sort_simple(li):
li_new = []
for i in range(len(li)):
min_val = min(li) # 找到最小的数，也需要遍历一边O(n)
li_new.append(min_val)
li.remove(min_val) # 按值删除，如果有重复的先删除最左边的,删除之后，后面元素需要向前移动补位，因此也是O(n)
return li_new
li = [3, 2, 4, 1, 5, 6, 8, 7, 9]
print(select_sort_simple(li))
"""
[1, 2, 3, 4, 5, 6, 7, 8, 9]
"""
注意这里的remove操作和min操作都不是O(1)的操作，都需要进行遍历，因此它的时间复杂度是O(n2)。
而且前面冒泡排序是原地排序不需要开启一个新的列表，二这个版本的选择排序不是原地排序，多占了一份内存。
（2）优化后的选择排序
def select_sort(li):
# 和冒泡排序类似，在n-1趟完成后，无序区只剩一个数，这个数一定是最大的
for i in range(len(li)-1): # i是第几趟
min_loc = i # 最小值的位置
for j in range(i+1, len(li)): # 遍历无序区，从i开始是自己跟自己比，因此从i+1开始
if li[j] < li[min_loc]: # 如果遍历的这个数小于现在min_loc位置上的数
min_loc = j # 修改min_loc的index，循环完后，min_loc一定是无序区最小数的下标
li[i], li[min_loc] = li[min_loc], li[i] # 将i和min_loc对应的值进行位置交换
print(li) # 打印每趟执行完的排序，分析过程
li = [3, 2, 4, 1, 5, 6, 8, 7, 9]
select_sort(li)
# print(li) # [1, 2, 3, 4, 5, 6, 7, 8, 9]
这里只有两层循环，时间复杂度是O(n2)。
3、插入排序（Insertion Sort）
元素被分为有序区和无序区两部分。初始时手里（有序区）只有一张牌，每次（从无序区）摸一张牌，插入到手里已有牌的正确位置，直到无序区变空。
（1）图示说明
一开始手里的牌只有5
第一张摸到的牌是7，比5大插到5的右边：
第二张摸到的牌是4，需要将5和7的位置向右挪，将4插到最前面：
后面的情况依次类推。
（2）代码示例
def insert_sort(li):
for i in range(1, len(li)): # i表示摸到牌的下标
tmp = li[i] # 摸到的牌
j = i - 1 # j指得是手里牌的下标
while li[j] > tmp and j >= 0: # 循环条件
"""
循环终止条件：如果手里最后一张牌 <= 摸到的牌 or j == -1
比如手里有牌457，新摸到一张6(index=3)，当比对5与6时，5<6,满足了循环终止条件，插到列表j+1处，即index=2处.
比如手里的牌是4567,新摸到一张3(index=4)，一个个比对均比3大，到4与3比较时，由于比4小，再次循环j=-1，满足终止条件插到列表j+1处，即最前面
"""
li[j + 1] = li[j] # 通过循环条件，将手里的牌左移
j -= 1 # 手里的牌对比箭头左移
li[j + 1] = tmp # 将摸到的牌插入有序区
print(li) # 打印每一趟排序过程
li = [3, 2, 4, 1, 5, 6, 9, 6, 8]
print('原列表', li)
insert_sort(li)
print('排序结果', li)
这个循环主要是在找插入的位置。
时间复杂度：O(n2)。
（3）查看排序算法执行时间和效率
准备好cal_time.py:
import time
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
检查10000个随机数字排序：
import random
from cal_time import *
@cal_time
def insert_sort(li):
for i in range(1, len(li)): # i表示摸到牌的下标
tmp = li[i] # 摸到的牌
j = i - 1 # j指得是手里牌的下标
while li[j] > tmp and j >= 0: # 循环条件
li[j + 1] = li[j] # 通过循环条件，将手里的牌左移
j -= 1 # 手里的牌对比箭头左移
li[j + 1] = tmp # 将摸到的牌插入有序区
# print(li) # 打印每一趟排序过程
li = list(range(10000))
random.shuffle(li)
insert_sort(li)
"""
insert_sort running time: 4.496495723724365 secs.
"""
4、快速排序（Quick Sort）
快速排序思路：取一个元素p（第一个元素），使元素p归位；列表被p分为两部分，左边都比p小，右边都比p大；递归完成排序。
算法关键点：归位、递归。
（1）图示说明
（2）元素归位过程分析
5要归位，先用一个变量将5存起来，两个箭头表示当前列表的left和right:
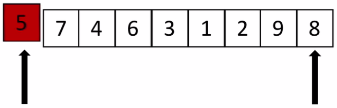
列表左边有了一个空位，从右边开始找一个比5小的数填入：
此时右边有了一个空位，右边是给比5大的数准备的，从左边开始找比5大的数填入：
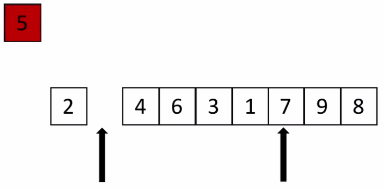
同理，此时左边又有了空位继续从右边开始找比5小的数填过去，以此类推
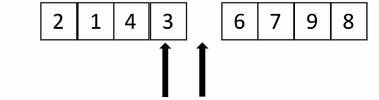
最后要找比5大的数放到右边去，但是3<5，这时left和right重合了，此时说明位置已经在中间了，将5放回。
（3）归位代码实现
def partition(li, left, right):
"""
归位函数
:param li: 列表
:param left: 左箭头
:param right: 右箭头
:return:
"""
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: # 从右边找一个比tmp小的数放过来
# 注意由于循环条件是li[right] >= tep，在两个箭头相遇时不会退出循环，因此添加left<right条件
right -= 1 # 如果比tmp大则right往左走一步
li[left] = li[right] # 将右边找的数插入到左边空位处
print(li) # 打印排序过程
while left<right and li[left] <= tmp: # 从左边找一个比tmp大的数放入右边的空位
left += 1 # 如果比tmp小则left往右走一步
li[right] = li[left] # 将左边的值写入到右边空位处
print(li) # 打印排序过程
# 循环终止条件：left>=right
li[left] = tmp # 将tmp归位
li = [5,7,4,6,3,1,2,9,8]
print("原列表", li)
partition(li, 0, len(li)-1)
print("排序结果", li)
"""
原列表 [5, 7, 4, 6, 3, 1, 2, 9, 8]
[2, 7, 4, 6, 3, 1, 2, 9, 8]
[2, 7, 4, 6, 3, 1, 7, 9, 8]
[2, 1, 4, 6, 3, 1, 7, 9, 8]
[2, 1, 4, 6, 3, 6, 7, 9, 8]
[2, 1, 4, 3, 3, 6, 7, 9, 8]
[2, 1, 4, 3, 3, 6, 7, 9, 8]
排序结果 [2, 1, 4, 3, 5, 6, 7, 9, 8]
"""
注意无论从左边找还是从右边找，都需要添加left<right条件，在箭头相遇时跳出循环。还可以注意到每次写入空位，并不是真正的空位，仍由原元素占位在空位出，直到tmp归位，整个列表才没有了重复的元素。
（4）快速排序代码实现
def partition(li, left, right):
"""
归位函数
:param li: 列表
:param left: 左箭头
:param right: 右箭头
:return:
"""
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: # 从右边找一个比tmp小的数放过来
# 注意由于循环条件是li[right] >= tep，在两个箭头相遇时不会退出循环，因此添加left<right条件
right -= 1 # 如果比tmp大则right往左走一步
li[left] = li[right] # 将右边找的数插入到左边空位处
print(li) # 打印排序过程
while left<right and li[left] <= tmp: # 从左边找一个比tmp大的数放入右边的空位
left += 1 # 如果比tmp小则left往右走一步
li[right] = li[left] # 将左边的值写入到右边空位处
print(li) # 打印排序过程
# 循环终止条件：left>=right
li[left] = tmp # 将tmp归位
return left
def quick_sort(li, left, right):
"""快速排序两个关键：归位、递归"""
if left < right: # 至少有两个元素
mid = partition(li, left, right)
quick_sort(li, left, mid-1)
quick_sort(li, mid+1, right)
li = [5,7,4,6,3,1,2,9,8]
quick_sort(li, 0, len(li)-1)
print(li)
注意这里使用了partition归位函数和快速排序递归框架完成了快速排序设计。
（5）快速排序的效率
快速排序的时间复杂度：O(nlogn)，每一层排序的复杂度是O(n)，总共有logn层。
（6）快速排序改写
想给quick_sort添加装饰器查看排序运行效率，但是递归函数不能添加装饰器，因此需要做如下改写：
from cal_time import *
def partition(li, left, right):......
def _quick_sort(li, left, right):
"""快速排序两个关键：归位、递归"""
if left < right: # 至少有两个元素
mid = partition(li, left, right)
_quick_sort(li, left, mid-1)
_quick_sort(li, mid+1, right)
@cal_time
def quick_sort(li):
_quick_sort(li, 0, len(li)-1)
（7）测试验证快排和冒泡排序执行效率
# -*- coding:utf-8 -*- __author__ = 'Qiushi Huang' import random from cal_time import * import copy # 复制模块 def partition(li, left, right): """ 归位函数 :param li: 列表 :param left: 左箭头 :param right: 右箭头 :return: """ tmp = li[left] while left < right: while left < right and li[right] >= tmp: # 从右边找一个比tmp小的数放过来 # 注意由于循环条件是li[right] >= tep，在两个箭头相遇时不会退出循环，因此添加left<right条件 right -= 1 # 如果比tmp大则right往左走一步 li[left] = li[right] # 将右边找的数插入到左边空位处 # print(li) # 打印排序过程 while left<right and li[left] <= tmp: # 从左边找一个比tmp大的数放入右边的空位 left += 1 # 如果比tmp小则left往右走一步 li[right] = li[left] # 将左边的值写入到右边空位处 # print(li) # 打印排序过程 # 循环终止条件：left>=right li[left] = tmp # 将tmp归位 return left def _quick_sort(li, left, right): """快速排序两个关键：归位、递归""" if left < right: # 至少有两个元素 mid = partition(li, left, right) _quick_sort(li, left, mid-1) _quick_sort(li, mid+1, right) @cal_time def quick_sort(li): _quick_sort(li, 0, len(li)-1) @cal_time def bubble_sort(li): for i in range(len(li)-1): # 总共是n-1趟 exchange = False for j in range(len(li)-i-1): # 每一趟都有箭头，从0开始到n-i-1 if li[j] > li[j+1]: # 比对箭头指向和箭头后面的那个数的值 # 当箭头所指数大于后面的数时交换位置, 升序排列；条件相反则为降序排列 li[j], li[j+1] = li[j+1], li[j] exchange = True # 如果发生了交换就置为true # print(li) if not exchange: # 如果exchange还是False，说明没有发生交换，结束代码 return li = list(range(10000)) random.shuffle(li) li1 = copy.deepcopy(li) # 深拷贝 li2 = copy.deepcopy(li) quick_sort(li1) bubble_sort(li2) """ quick_sort running time: 0.03162503242492676 secs. bubble_sort running time: 10.773478269577026 secs. """ print(li1) # [0, 1, 2, 3, 4,..., 9997, 9998, 9999] print(li2)
对比运行时间，可以发现针对10000个元素的数组排序，快速排序的效率比冒泡排序高了几百倍。
时间复杂度O(nlogn)和O(n2)在数量越大的情况下，效率相差将越来越大。
快速排序的最好情况时间复杂度是O(n)，一般情况时间复杂度是O(nlogn)，最坏情况时间复杂度是O(n2)。
（8）快速排序存在的问题
首先python有一个递归最大深度的问题，默认是999，修改递归最大深度方法：
import sys sys.setrecursionlimit(100000) # 修改递归最大深度
虽然可以修改；而且递归会相当消耗一部分的系统资源。
其次快速排序有一个最坏情况出现：倒序排列的数组，在这种情况下，快速排序无法两边同时排序，每次只能排序一个数字。因此在这种情况下快速排序的时间复杂度是：O(n2)。
加入随机化解决该问题：即不再找第一个元素归位，而是随机找一个值与第一个元素交换，然后继续执行快速排序，就可以解决倒序例子时间复杂度特别高的情况。但是这个方法不能完全避免最坏情况，比如每次随机都恰好选中了最大的一个数，但是这种修改可以让最坏情况无法被设计出来，发生最坏情况的概率也会非常非常小。
5、堆排序（Heap-Sort）
6、归并排序（Merge-Sort）
三、排序总结
1、冒泡排序、选择排序、插入排序
冒泡排序、选择排序、插入排序的时间复杂度都是O(n2)，且都是原地排序。
2、快速排序、堆排序、归并排序
快速排序、堆排序、归并排序这三种排序算法的时间复杂度都是O(nlogn)。 但有常数差异。
（1）一般情况下，就运行时间来比较：
快速排序（速度最快）< 归并排序 < 堆排序
（2）三种排序算法的缺点：
快速排序：极端情况下排序效率低。
归并排序：需要额外的内存开销。
堆排序：在快的排序算法中相对较慢。
3、六种排序算法对比总结
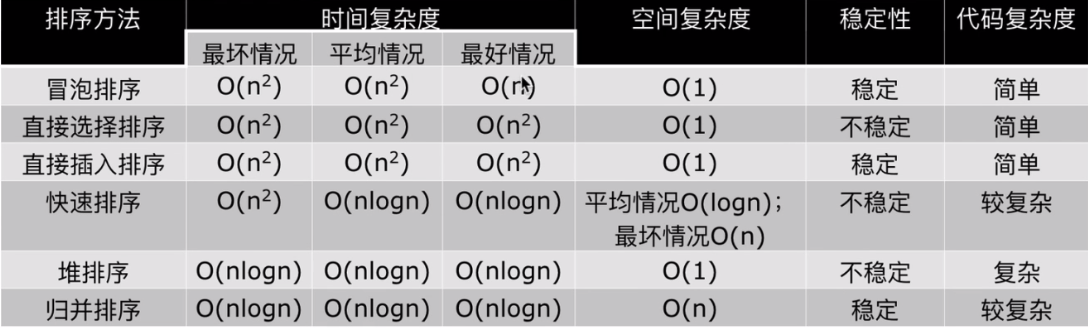
（1）递归占用空间
递归需要用系统占的空间，快速排序在平均情况下需要递归logn层，所以平均情况下需要消耗O(logn)的空间复杂度；最坏情况下需要递归n层，因此需要消耗O(n)的时间复杂度。
归并虽然也有递归，但他已经开了一个列表了占用O(n)，归并递归需要的空间复杂度是O(logn)小于O(n)，因此统计空间复杂度是O(n)。
（2）排序算法稳定性
假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
判断是否算法是否稳定：挨着换的稳定，不挨着换的不稳定。
（3）代码复杂度
算法是否好写，是否容易理解。
