线性回归算法实验分析

一、线性回归实验目标

　　算法推导过程中已经给出了求解方法，基于最小乘法直接求解，但这并不是机器学习的思想，由此引入了梯度下降方法。

　　实验主要内容：

　　（1）线性回归方程实现

　　（2）梯度下降效果

　　（3）对比不同梯度下降测量

　　（4）建模曲线分析

　　（5）过拟合与欠拟合

　　（6）正则化的作用

　　（7）提前停止策略

二、实验步骤

　　首先准备环境，配置画图参数，过滤警告。

import numpy as np
import os
import warnings
import matplotlib
import matplotlib.pyplot as plt

# 画图参数设置
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

# 过滤警告
warnings.filterwarnings('ignore')

　　构造数据点（样本）：

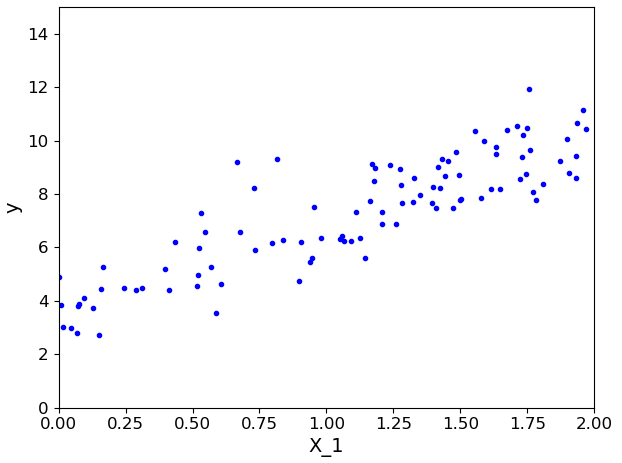
# 通过rand函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1
X = 2 * np.random.rand(100, 1)
# 构造线性方程，加入随机抖动
# numpy.random.randn()是从标准正态分布中返回一个或多个样本值
# 1.当函数括号内没有参数时，返回一个浮点数；
# 2.当函数括号内有一个参数时，返回秩为1的数组，不能表示向量和矩阵
# 3.当函数括号内有两个及以上参数时，返回对应维度的数组，能表示向量或矩阵。np.random.randn(行,列)
# 4.np.random.standard_normal()函数与np.random.randn类似，但是输入参数为元组（tuple）
y = 3*X + 4 + np.random.randn(100, 1)

plt.plot(X, y, 'b.')     # b指定为蓝色,.指定线条格式
plt.xlabel('X_1')
plt.ylabel('y')

# 设置x轴为0-2，y轴为0-15
plt.axis([0, 2, 0, 15])
plt.show()

　　执行显示数据点如下所示：

　　

1、线性回归方程实现

　　

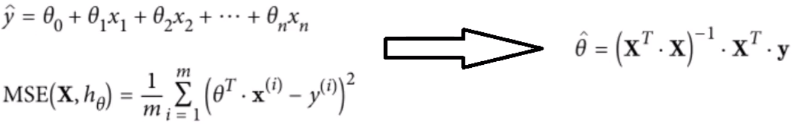
"""线性回归方程实现"""
# numpy.c_:按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。
# numpy.r_:按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。
# ones()返回一个全1的n维数组，同样也有三个参数：shape（用来指定返回数组的大小）、dtype（数组元素的类型）、order（是否以内存中的C或Fortran连续（行或列）顺序存储多维数据）。后两个参数都是可选的，一般只需设定第一个参数。
X_b = np.c_[(np.ones((100, 1)), X)]
# np.linalg.inv:矩阵求逆
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)
'''
[[3.99844262]
 [3.09461187]]
'''

# 测试数据
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
# 预测结果
y_predict = X_new_b.dot(theta_best)
print(y_predict)

plt.plot(X_new, y_predict, 'r--')   # 指定红色和线条
plt.plot(X, y, 'b.')     # 指定蓝色和点
plt.axis([0, 2, 0, 15])
plt.show()

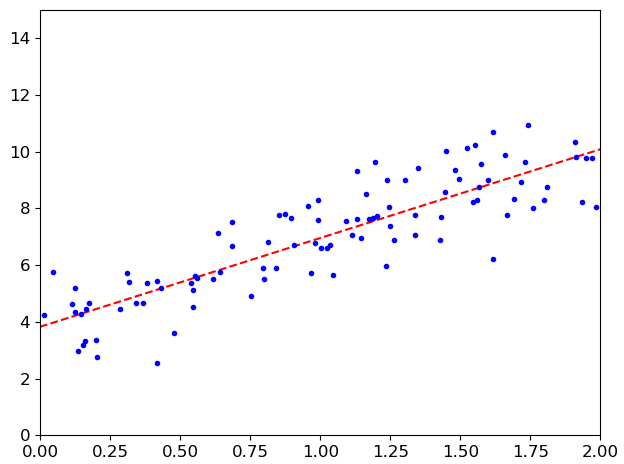
　　执行显示效果：

　　

（1）np.c_和np.r_

　　numpy.c_：按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。
　　numpy.r_：按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。

（2）numpy.linalg模块

　　numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。

• np.linalg.inv()：矩阵求逆
• np.linalg.det()：矩阵求行列式（标量）

（3）ones函数

　　ones()返回一个全1的n维数组，同样也有三个参数：shape（用来指定返回数组的大小）、dtype（数组元素的类型）、order（是否以内存中的C或Fortran连续（行或列）顺序存储多维数据）。后两个参数都是可选的，一般只需设定第一个参数。

（4）dot函数

　　dot()返回的是两个数组的点积(dot product)

　　1.如果处理的是一维数组，则得到的是两数组的內积；

　　2.如果是二维数组（矩阵）之间的运算，则得到的是矩阵积（mastrix product）。所得到的数组中的每个元素为，第一个矩阵中与该元素行号相同的元素与第二个矩阵与该元素列号相同的元素，两两相乘后再求和。

　　3.dot()函数可以通过numpy库调用，也可以由数组实例对象进行调用。a.dot(b) 与 np.dot(a,b)效果相同。

2、slearn实现线性回归

# sklearn线性回归实现
from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()    # 线性回归实例化
lin_reg.fit(X, y)     # 拟合线性模型
print(lin_reg.intercept_)   # intercept_:线性模型中的独立项
print(lin_reg.coef_)        # coef_:线性回归的估计系数
"""
[3.92151171]
[[2.98627461]]
"""

　　可以看到得出的结果和前面计算的 theta_best 相同。

3、梯度下降

　　

 

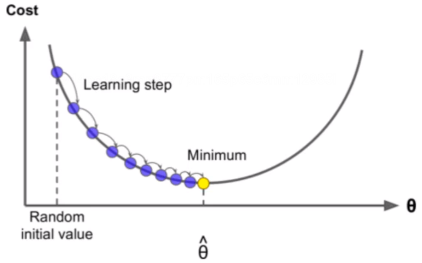
　　选择一个初始值，沿着一个方向去走。

（1）步长问题

　　步长太小：收敛速度太慢，等不起。

　　

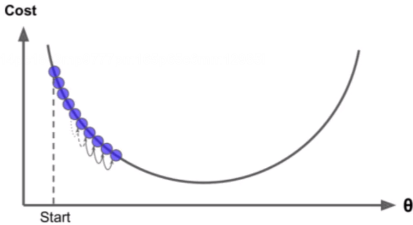
　　步长太大：得到的结果不准确

　　

（2）收敛的问题

　　有可能是找到的是局部的最低点，而不是全局的最低点。

　　

 

（3）标准化的作用

　　消除数据的量纲，这个过程叫做无量纲化。

　　无量纲化：我们的数据一般都是有单位的，比如身高的单位有m，cm，这个无量纲化并不是说把m变成cm，而是说，无论是m还是cm，最后都会变成1，也就是没有了单位。比如 当前身高的单位为cm，经过这个式子的处理变成了一个没有单位的数字。

　　当两个特征的量级差别很大的时候，这样的操作是有意义的，假如你有身高和体重两个个特征。身高的单位是m，它的取值经常是这样的值：1.65,1,70,1.67等，而体重的单都位是kg，它经常取这样的值：53,68,73等，我们可以看到体重的值要远远大于身高的值，它们已经不是一个量级了。进行数据的缩放可以避免我们的结果由取值较大的特征决定。

　　加快模型的收敛速度

　　

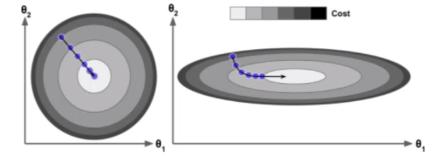
　　在上图当中，左边表示在没有进行缩放以前模型的收敛情况，右边表示在进行缩放以后模型收敛的情况。在SVM、线性回归还有PCA当中经常用到。

　　数据的标准化Standardization，也叫作（去中心化+方差缩放）,通过把一组数据的均值变为0，方差变为1实现数据的缩放。数据的标准化是我们对数据的进行缩放的时候最容易想到的操作，也是最常用到的操作。它也叫z-score方法。