logistic回归介绍以及原理分析
1.什么是logistic回归?
logistic回归虽然说是回归,但确是为了解决分类问题,是二分类任务的首选方法,简单来说,输出结果不是0就是1
举个简单的例子:
癌症检测:这种算法输入病理图片并且应该辨别患者是患有癌症(1)或没有癌症(0)
2.logistic回归和线性回归的关系
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。
逻辑回归假设因变量 y 服从二项分布,而线性回归假设因变量 y 服从高斯分布。
因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。
可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
换种说法:
线性回归,直接可以分为两类,
但是对于图二来说,在角落加上一块蓝色点之后,线性回归的线会向下倾斜,参考紫色的线,
但是logistic回归(参考绿色的线)分类的还是很准确,logistic回归在解决分类问题上还是不错的


3.logistic回归的原理
Sigmoid函数:
曲线: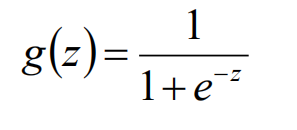
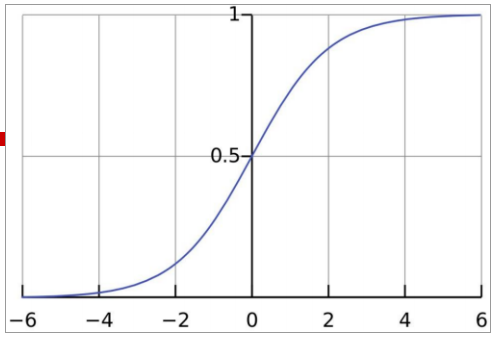
之后推导公式中会用到:

我们希望随机数据点被正确分类的概率最大化,这就是最大似然估计。
最大似然估计是统计模型中估计参数的通用方法。
你可以使用不同的方法(如优化算法)来最大化概率。
牛顿法也是其中一种,可用于查找许多不同函数的最大值(或最小值),包括似然函数。也可以用梯度下降法代替牛顿法。
既然是为了解决二分类问题,其实也就是概率的问题,分类其实都是概率问题,
那咱们先看个概率的问题:
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。
我们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。
现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。
这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。
假如在前面的一百次重复记录中,
有七十次是白球,请问罐中白球所占的比例最有可能是多少?
解答:
假设白球的概率是p,黑球的概率是1-p
取出100个球,70是白球,30个是黑球,概率:p**70*(1-p)**30
要求出白球所占比例最有可能是多少,其实就是最大似然估计,求导令导函数等于0,求出概率
𝑓(𝑝)=𝑝70∗(1−𝑝)30
70∗𝑝69∗(1−𝑝)30+𝑝70∗30∗(1−𝑝)29∗(−1)=0
70∗(1−𝑝)−𝑝∗30=0
同理一下,logistic回归解决二分类问题,跟这个概率问题很相似,logistic回归也是求概率最大,使用的同样是似然函数
假定:
y=1和y=0的时候的概率
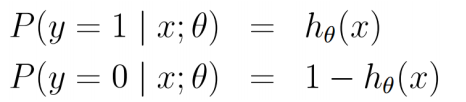
![]()
似然函数:其实就是概率相乘,然后左右两边同时取对数
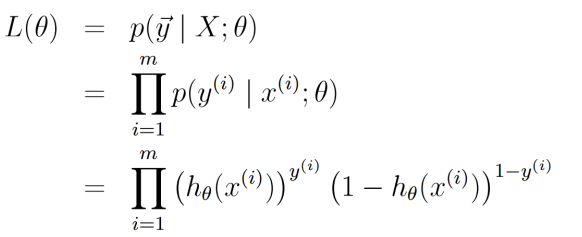
![]()
对数似然函数,求导,得到θ的梯度
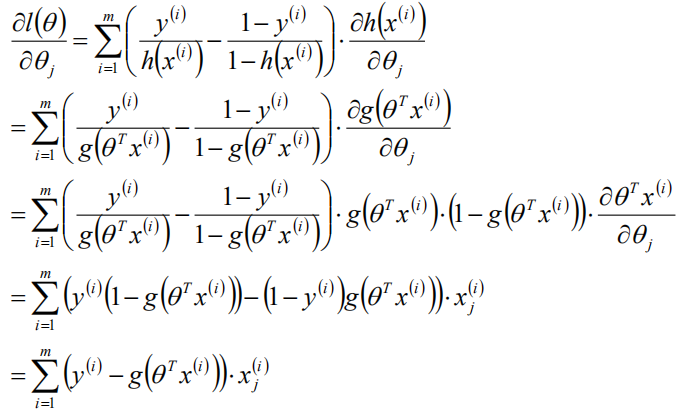
因为P=g(θX),P其实是θ的函数,X已知,要想P越大,就要θ越大,梯度上升问题
得到θ的学习规则:α为学习率
![]()
最后将θ带入h(x)函数,求出概率
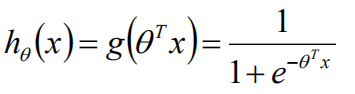
总结来说:
比较一下logistic回归的参数学习规则和线性回归的参数学习规则
两个都是如下,形式一样,只是不同的是
线性回归 h(x)=θX
logistic回归 ![]()
一个使用的模型是线性函数,一个使用的是sigmoid函数
![]()
4.logistic回归的使用
对于鸢尾花分类案例,计算概率,鸢尾花有三种类别,使用三次logistic回归即可
# 导包
import numpy as np from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split
# 加载数据 X,y = datasets.load_iris(True) # logistic回归解决的是二分类问题,所以先剔除一个种类 cond = y!=2 X = X[cond] y = y[cond] # 划分训练数据和测试数据 result = train_test_split(X,y,test_size = 0.2) result
lr = LogisticRegression() # 训练数据 lr.fit(result[0],result[2]) 求出w斜率和b截距的值 w = lr.coef_ b = lr.intercept_ print(w,b)
# 预测一下概率 proba_ = lr.predict_proba(result[1]) proba_
得到的预测结果:

# 手动计算概率 h = result[1].dot(w[0].T) + b # 类别1的概率,p;另一类的概率是 1-p # sigmoid函数中计算概率 p = 1/(1 + np.e**(-h)) np.c_[1-p,p]
计算得到的结果,相同的

5.logistic回归的损失函数:
其实就是似然函数加个负号

5.logistic回归的优缺点:
Logistic 回归是一种被人们广泛使用的算法,因为它非常高效,不需要太大的计算量,又通俗易懂,不需要缩放输入特征,不需要任何调整,且很容易调整,并且输出校准好的预测概率。
与线性回归一样,当你去掉与输出变量无关的属性以及相似度高的属性时,logistic 回归效果确实会更好。因此特征处理在 Logistic 和线性回归的性能方面起着重要的作用。
Logistic 回归的另一个优点是它非常容易实现,且训练起来很高效。在研究中,我通常以 Logistic 回归模型作为基准,再尝试使用更复杂的算法。
由于其简单且可快速实现的原因,Logistic 回归也是一个很好的基准,你可以用它来衡量其他更复杂的算法的性能。
它的一个缺点就是我们不能用 logistic 回归来解决非线性问题,因为它的决策边界是线性的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号