数据结构和算法_02时间复杂度和空间复杂度

高级语言编写的程序在计算机上运行时所消耗的时间取决于下列因素：

1.算法采用的策略，方案；

2.编译产生的代码质量(编译器)；

3.问题的输入规模(输入量的多少)；

4.机器执行指令的速度。

研究算法的复杂度，侧重的是研究算法随着输入规模扩大增大量的一个抽象！！

一、算法时间复杂度概念

一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数， 用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函 数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

这种用大写O()来体现算法时间复杂度的激发，我们称之为大O记法。

分析：随着模块n的增大，算法执行的时间的增长率和 f(n) 的增长率成正比，所以 f(n) 越小，算法的时间复杂度越低，算法的效率越高。

 

1、推导大O阶方法(如果分析一个算法的时间复杂度)：

1）用常数1取代运行时间中的所有加法常数

2）在修改后的运行次数中，只保留最高项(如：2 + 2n + n^2 + n^3，则保留n^3)

3）如果最高阶项存在且不是1，则去除与这个项相乘的常数(如：3n^3，则保留n^3)

4）得到的最后结果就是大O阶

 

• 常数阶：

    int sum = 0, n = 100;
    printf("I'll move on.\n");
    printf("I'll move on.\n");
    printf("I'll move on.\n");
    printf("I'll move on.\n");
    printf("I'll move on.\n");
    printf("I'll move on.\n");

上面代码的大O阶并不是O(8)，按照概念"T(n)是关于问题规模n的函数来说"、"1)"证明，O(1)才是正确答案;

 

• 线性阶：

一般含有非嵌套循环涉及线性阶，线性阶就是随着问题规模n的扩大，对应计算次数呈直线增长。

    int i, sum = 0, n = 100;
    
    for (i = 0; i < n; i ++ ) {
        sum += i;
    }

上面这段代码，它的循环的时间复杂度为O(n)，因为循环体中代码需要执行n次。

 

• 平方阶：

    int i, j, n = 100;
    for (i = 0; i < n; i ++ ) {
        for (j = 0; j < n; j ++) {
            printf("I'll move on.\n");
        }
    }

n等于100，也就是说外层循环每执行一次，内层循环就执行100次，那总共想要从这两个循环出来，需要执行100*100次，也就是n的平方。所以这段代码的复杂度为 O(n^2)。

如果三个嵌套循环，那就是n^3。所以我们就可以得出结论：循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。

 

    int i, j, n = 100;
    for (i = 0; i < n; i ++ ) {
        for (j = i; j < n; j ++) { // 此处j=i
            printf("I'll move on.\n");
        }
    }

分析该代码，最后执行的次数为：n * (n + 1) /2 = n^2/2 + n/2;

使用推导大O阶的攻略，第一条忽略(没有常数相加)。第二条只保留最高项(去掉)。第三条，去除与最高项相乘的常数，最终得O(n^2)。

 

• 对数阶：

    int i = 1, n = 100;
    while (i < n) {
        i = i * 2;
    }
    printf("%d", i);

假设有x个2相乘后大于或等于n，则退出循环。

得到 2^x = n → x = log(2)n，所以这个循环的时间复杂度为 O(logn)。

 

函数调用的时间复杂度分析：

1）

// 大O阶为 O(1)
void function(int count) {
    printf("%d", count);
}


int main(int argc, const char * argv[]) {
    
    // 大O阶为O(n)
    int i, n = 100;
    for (i = 0; i < n; i ++) {
        function(i);
    }
    
    return 0;
}

 

 2）

// 大O阶为 O(n)
void function(int count) {
    // 大O阶为O(n)
    int j, n = 100;
    for (j = 0; j < n; j ++) {
        printf("%d", j);
    }
}

int main(int argc, const char * argv[]) {
    
    // 大O阶为O(n^2)
    int i, n = 100;
    for (i = 0; i < n; i ++) {
        function(i);
    }
    
    return 0;
}

 

常见的时间复杂度：

 

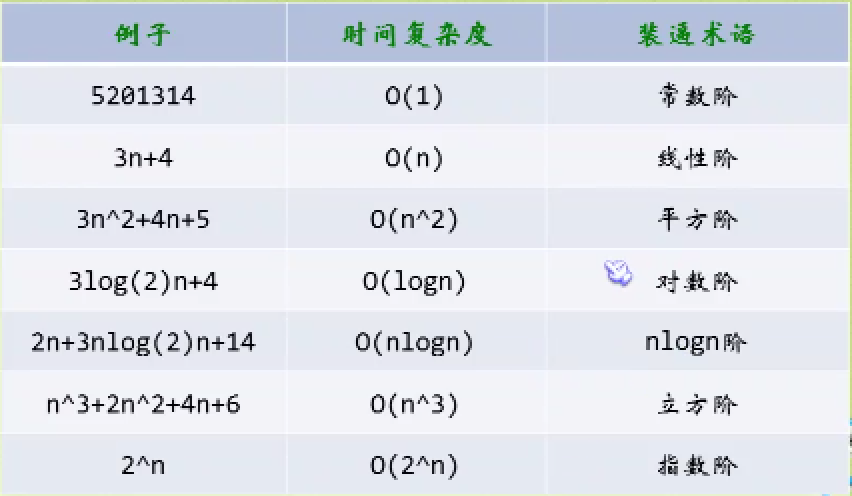
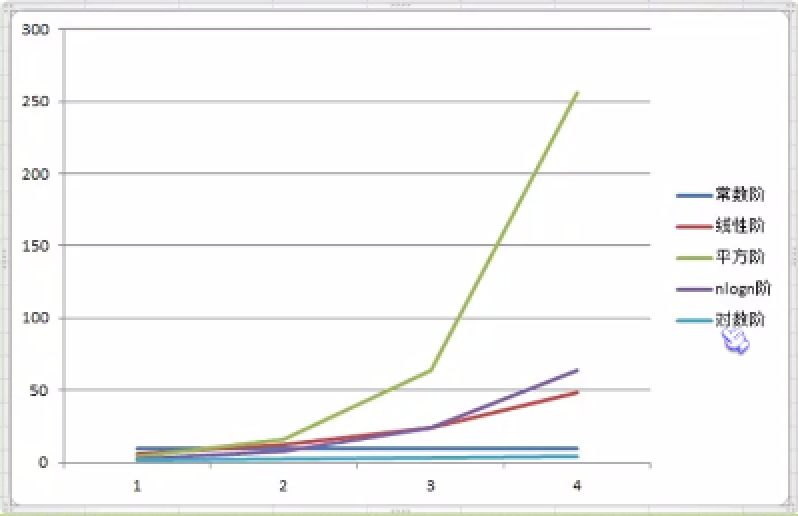
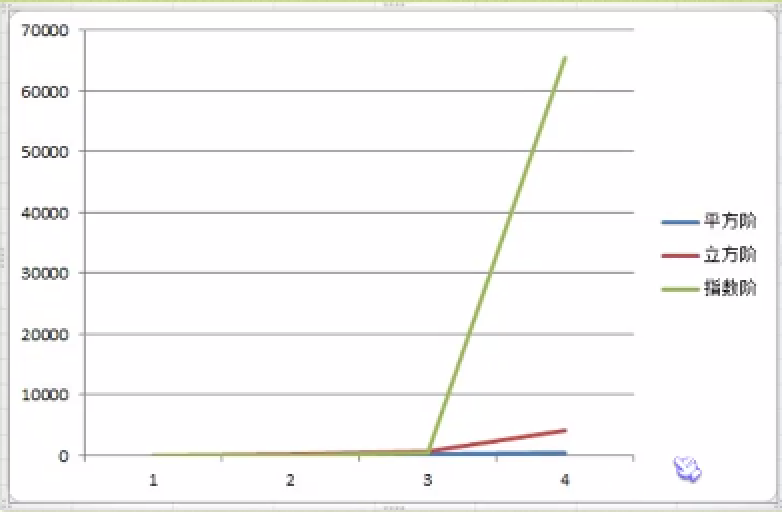
 常用的时间复杂度所耗费的时间从小到大依次是：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n).

最坏情况与平均情况：

平均运行时间是期望的运行时间。

最坏运行时间是一种保证。在应用中，这是一种最重要的需求，通常除非特别指定，我们提到的运行时间都是最坏情况的运行时间。

 

二、算法的空间复杂度

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。

通常所说的复杂度指的是时间复杂度！

 尊重作者劳动成果，转载请注明： 转载自【kingdev】