算法题：ID数量

目录

• 题目描述
• 示例
• Java解答

注意

1.在何处取余不影响结果正确性？

对乘法和加法的运算表达式里取余都不会，因为有取模运算的分配律

(a * b) mod m = [(a mod m) * (b mod m)] mod m

(a * b) mod m = [(a mod m) * (b mod m)] mod m

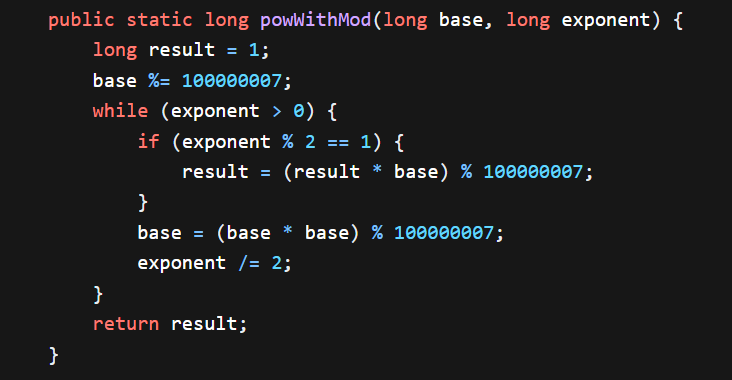
2.不建立数组，用快速幂可以吗
快速幂也可以

题目描述

大学生小名设计了一种语言，他的语言最大支持N个字不同的字符，
并且他规定了由这些字符组成的ID，任何ID的长度需要大于等于1月小于等于L个字符，
他希望设计一个程序，计算他的语言总共能组成多少个ID

例如，当N=2(假设字符可以是0或1)，并且L=3时，他具有如下的ID:{0,1,00,01,10,11,000,001,010,011,100,101,110,111},因此当N=2,L=3时总共有14种
ID。你需要编写一个程序，可以帮助小明找到可能的ID的总数

由于答案可能非常大，最后的结果需要对1000000007取余。

示例

输入

2 3
100 15
0 0

输出

14
979451521

Java解答

import java.util.Scanner;

public class CompilerLanguageIDCounter {
    private static final int MOD = 1000000007;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            int N = scanner.nextInt();
            int L = scanner.nextInt();
            if (N == 0 && L == 0) {
                break;
            }
            System.out.println(countIDs(N, L));
        }
        scanner.close();
    }

    private static long countIDs(int N, int L) {
        // dp[i] 表示长度为 i 的ID的数量
        long[] dp = new long[L + 1];
        dp[1] = N; // 长度为1的ID有N个

        // 计算长度从2到L的所有ID数量
        for (int i = 2; i <= L; i++) {
            dp[i] = (dp[i - 1] * N) % MOD;
        }

        // 累加所有长度的ID数量
        long total = 0;
        for (long count : dp) {
            total = (total + count) % MOD;
        }

        return total;
    }
}