解密ln( )函数

感谢理解完指数函数（指数函数和自然对数），下一个目标就是对数函数。数学中对自然对数的定义是的逆运算，但有一个更形象的理解：自然对数刻画了复合利率的增长时间

假设你的投资有100%的回报率，并保持复利。如果你想获得10倍的增长，那么你只需要等待年。接下来我将给大家解释为什么是这个数字。

e 的指数函数和自然对数互为逆运算：

可别被费解的名词解释吓到！深吸一口气，跟随笔者一道，让我们进入e的内部一探究竟！

e--关于增长
正如我们上次所说的那样，描述了复合增长率乘以时间的情形：连续3年保持100%的增长，和在1年里有300%的增长，最终效果是一样的。

我们可以使用任意的复合利率和时间，将其转化为利率为100%时所需要的时间。这样我们就只需要考虑时间分量。

例如：

在50%的增长率下增长4年，可以转化为在100%的增长率下增长2年。即：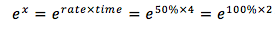



所以，含义是：

ln--关于时间

自然对数是的逆运算，那么逆运算是什么意思呢？



例如：

假设增长率为100%，我们有：





自然对数并不“自然”


什么是ln(1)呢？我需要多少天的复利增长才能获得原总数的1倍。答案很显然：0。

那么小数值会是怎么样的呢？我们需要花多少时间来增长到0.5倍呢？假设我们的复合利率仍为100%，那么我们知道就是得到两倍东西所需要的时间。”增长到0.5倍“也就是说：倒退到现有金钱的一半所需要的时间，即：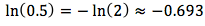

其中，负数的意思就是时间倒退，即我们需要倒退约为0.693个单位时间就会回到现在金钱的一半。一般来说，我们可以求该小数或者分数的倒数来求得倒退所需的时间。



再进行一次思维实验：假设你有一笔金钱，它如何从1增长到-3倍呢？



显然这是不可能的，我们拥有的金钱数只能大于或等于0。所以对于自然对数来说，负数是没有定义的。




有趣的对数乘法


我需要花多少时间来增长到40倍呢？综上所述，问题转化成符号式即为。但是，我们换种思考方式，我们可以把40倍的增长看作先从1增长到4，即：先翻4倍，然后再从4增长到40，即：再翻10倍。即：


任何数字都可以这样拆开，如：要增长到原来的20倍，那么，就可以看成先增长2倍再增长10倍，或者先找找5倍再增长4倍等等。



不失一般性：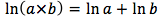




不失一般性：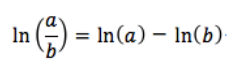

 

我们可以看到，看似抽象的数学符号，背后都蕴含着实际的意义




自然对数在复利中的使用


到这里你已经基本明白了自然对数，但是你仍然会问，上述问题都是假设复合利率是100%，但是更多的时候我们的复合增长率不是100%，而是其他数值，如5%，那么怎么办呢？



Ok，没问题，我们的ln( )实际上是由利率和时间复合而成的，他就是上篇文章我们说到中的x。只是我们假设复利为100%使得我们的问题更容易理解，但是我们仍然可以使用任何的利率。

 

显然，我们以100%的增长率增长30倍需要3.4年，如果增长率大一倍，则时间就会短一半，如果增长率变小了，则时间也会变长。



有趣！他们的结果都是相同的对么？自然对数可以使用任何的利率和时间，你可以修改任何你想修改的变量。




关于ln（e）


最后给大家一个小小问题看看大家理解了没有呢？即ln（e）是什么意思呢？

数学家可能会回答：因为自然对数是e的逆，所以

看了这篇文章的你可能会回答：ln（e）是获得e倍所需要的时间，而e是单位时间的增长倍数，所以ln（e）=1
---------------------
作者：算法与数学之美
来源：CSDN
原文：https://blog.csdn.net/FnqTyr45/article/details/78557351
版权声明：本文为博主原创文章，转载请附上博文链接！