吴恩达机器学习系列课程--个人笔记
网址:https://www.bilibili.com/video/av50747658/ (b站找的有中文字幕的视频)
第一周
一、引言
1.1 欢迎
1.2 机器学习是什么
1.3 监督学习
1.4 无监督学习
二、单变量线性回归
2.1 模型表示
2.2 代价函数
2.3 代价函数的直观理解 I
2.4 代价函数的直观理解 II
2.5 梯度下降
2.6 梯度下降的直观理解
2.7 梯度下降的线性回归
2.8 接下来的内容
三、线性代数回顾
3.1 矩阵和向量
3.2 加法和标量乘法
3.3 矩阵向量乘法
3.4 矩阵乘法
3-5 矩阵乘法特征
(1)矩阵乘法不适用交换律
(2)矩阵乘法满足结合律
(3)单位矩阵是对角线(a11,a22,a33...)都等于1的矩阵
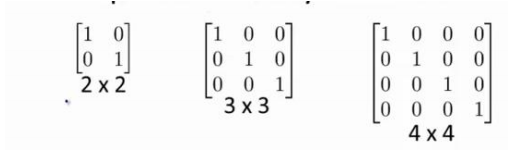
3-6 逆和转置
(1)逆矩阵
只有m*m的矩阵有逆矩阵

I是单位矩阵
(2)转置
aij的矩阵,变成aji
第2周
四、多变量线性回归
4-1 多功能
当用多个参数预测房价时,需使用多元线性回归,向量表示为:
4-2 多元梯度下降法
4-3 梯度下降法实践 1-特征缩放
4-4 梯度下降法实践 2-学习率
4-5 特征和多项式回归
4-6 正规方程
4-7 正规方程及不可逆性(可选)
五、Octave教程
5-1 基本操作
~= 表示 逻辑不等于
5-2 移动数据
5-3 计算数据
5-4 数据绘制
5-5 控制语句:for while if 语句
5-6 矢量(没太看懂)
第三周
六、逻辑回归
6-1 分类
逻辑回归算法(logistics regression)——逻辑回归算法是个分类算法,它适用于y值取离散值得情况。
二元分类(0,1分类)
6-2 假设陈述
6-3 决策界限
6-4 代价函数
6-5 简化代价函数与梯度下降
6-6 高级优化
学完本章需要实现:写一个函数,它能返回代价函数值、梯度值,因此要把这个应用到逻辑回归或者甚至线性回归中,你也可以把这些优化算法用于线性回归,你需要做的就是输入合适的代码来计算这里的这些东西。
6-7 多元分类——一对多
y值是多个分类值
七、正则化
7-1 过拟合问题
什么是过拟合
正则化
7-2 代价函数
7-3 线性回归的正则化
7-4 逻辑回归的正则化
---------------------------------------
第四周
八、神经网络:表述
8-1 非线性假设
8-2 神经元与大脑
8-3 模型展示I
8-4 模型展示II
8-5 例子与直觉理解I
8-6 例子与直觉理解II
8-7 多元分类
9-1 代价函数
9-2 反向传播算法
9-3 理解反向传播算法
9-4 使用注意:展开参数
9-5 梯度检测
9-6 随机初始化
9-7 组合到一起
9-8 无人驾驶
10-1 决定下一步做什么
10-2 评估假设
10-3 模型选择和训练、测试、验证集
60% 20% 20% 划分这三个集合(常用)
10-4 诊断偏差与方差
10-5 正则化和方差、偏差
10-6 学习曲线
10-7 决定接下来要做什么
11-1 确定执行的优先级
11-2 误差分析
11-3 不对称性分类的误差评估
11-4 精确度和召回率的权衡
11-5 机器学习数据
12-1 优化目标
12-2 直观上对大间隔的理解
12-3 大间隔分类器的数学原理
12-4 核函数1
12-5 核函数2
12-6 使用SVM
13-1 无监督学习
聚类
13-2 K-Means算法
13-3 优化目标
13-4 随机初始化
13-5- 选取聚类数量
14-1 目标I:数据压缩
14-2 目标II:可视化
14-3 主成分分析问题规划1
14-4 主成分分析问题规划2
14-5 主成分数量选择
14-6 压缩重现
14-7 应用PCA的建议
15-1 问题动机
15-2 高斯分布(正态分布)
15-3 算法
15-4 开发和评估异常检测系统
15-5 异常检测 VS 监督学习
当正样本过少,负样本较多的时候,使用异常检测,算法可以从负样本中学到足够多的特征
反之,负样本过少的时候,用监督学习
15-6 选择要使用的功能
15-7 多变量高斯分布
15-8 使用多变量高斯分布的异常检测
16-1 问题规划
推荐系统
16-2 基于内容的推荐算法
16-3 协同过滤
16-4 协同过滤算法
16-5 矢量化:低秩矩阵分解
16-6 实施细节:均值规范化
17-1 学习大数据集
17-2 随机梯度下降
17-3 Mini-Batch 梯度下降
17-4 随机梯度下降收敛
17-5 在线学习
17-6 减少映射与数据并行
18-1 问题描述与OCR.pipeline
图像识别
18-2 滑动窗口
使用滑动窗口检测器找出图片中的行人
18-3 获取大量数据和人工数据
18-4 天花板分析:下一步工作的pipeline
19-1 总结与感谢

