迷宫问题

7-9 求解迷宫从入口到出口的路径 (15分)

求解迷宫从入口到出口的路径。输入一个迷宫，求从入口通向出口的可行路径。为简化问题，迷宫用二维数组 int maze[10][10]来存储障碍物的分布，假设迷宫的横向和纵向尺寸的大小是一样的，并由程序运行读入, 若读入迷宫大小的值是n（3<n<=10），则该迷宫横向或纵向尺寸都是n，规定迷宫最外面的一圈是障碍物，迷宫的入口是maze[1][1]，出口是maze[n-2][n-2], 若maze[i][j] = 1代表该位置是障碍物，若maze[i][j] = 0代表该位置是可以行走的空位（0<=i<=n-1, 0<=j<=n-1）。求从入口maze[1][1]到出口maze[n-2][n-2]可以走通的路径。要求迷宫中只允许在水平或上下四个方向的空位上行走，走过的位置不能重复走，规定必须按向右、向下、向左、向上的顺序向前搜索试探。 如下这样一个迷宫：

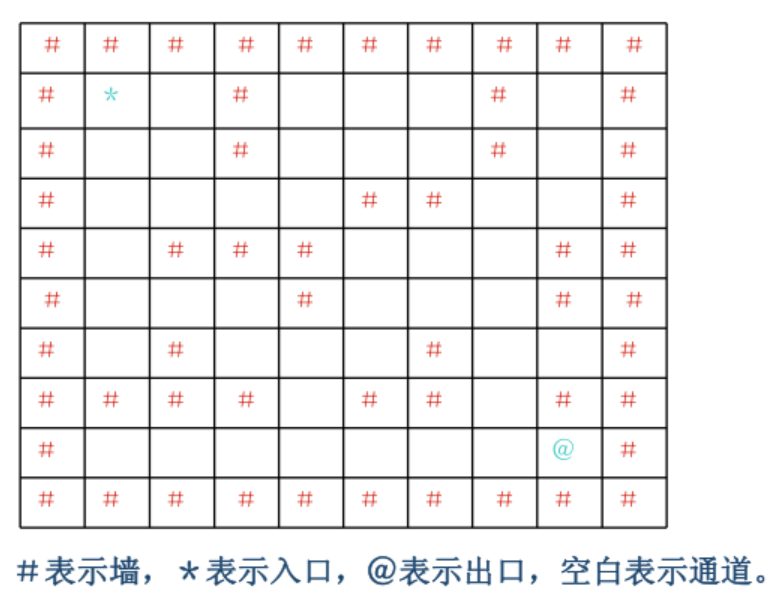
对应的二维数组表示：
int maze[10][10]={ {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,1,1}, {1,0,0,0,1,0,0,0,1,1}, {1,0,1,0,0,0,1,0,0,1}, {1,1,1,1,0,1,1,0,1,1}, {1,0,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1}};

输入格式:
输入迷宫大小的整数n, 以及n行和n列的二维数组（数组元素1代表障碍物，0代表空位）。

输出格式:
依次输出从入口到出口可行路径每个位置的行列下标（i,j），每个位置间用“,”分隔。若没有通路，输出：NO。

输入样例1:

4
1 1 1 1
1 0 1 1
1 0 0 1
1 1 1 1

输出样例1:

(1,1)(2,1)(2,2)

输入样例2:

10
1 1 1 1 1 1 1 1 1 1
1 0 0 1 0 0 0 1 0 1
1 0 0 1 0 0 0 1 0 1
1 0 0 0 0 1 1 0 0 1
1 0 1 1 1 0 0 0 0 1
1 0 0 0 1 0 0 0 0 1
1 0 1 0 0 0 1 0 0 1
1 0 1 1 1 0 1 1 0 1
1 1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1

输出样例2:

(1,1)(1,2)(2,2)(3,2)(3,1)(4,1)(5,1)(5,2)(5,3)(6,3)(6,4)(6,5)(7,5)(8,5)(8,6)(8,7)(8,8)

实验代码（栈）

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define MaxSize 100

typedef struct
{
	int i, j;
	int di;
}Box;

typedef struct
{
	Box data[MaxSize];
	int top;
}StType;

int maze[MaxSize][MaxSize];  //迷宫数组

void InitStack(StType*& s)  //初始化栈
{
	s = (StType*)malloc(sizeof(StType));
	s->top = -1;
}

void DestroyStack(StType*& s)  //销毁栈
{
	free(s);
}

bool StackEmpty(StType* s)  //判断栈是否为空
{
	return (s->top == -1);
}

bool Push(StType*& s, Box e)  //进栈
{
	if (s->top == MaxSize - 1)
		return false;
	s->top++;
	s->data[s->top] = e;
	return true;
}

bool Pop(StType*& s, Box& e)  //出栈
{
	if (s->top == -1)
		return false;
	e = s->data[s->top];
	s->top--;
	return true;
}

bool GetTop(StType*& s, Box& e)  //取栈顶元素
{
	if (s->top == -1)
		return false;

	e = s->data[s->top];
	return true;
}

bool mgpath(int xi, int yi, int xe, int ye)  //迷宫算法
{
	Box path[MaxSize], e;
	int i, j, di, i1, j1, k;
	bool find;
	StType* st;

	InitStack(st);
	e.i = xi; 
	e.j = yi;
	e.di = -1;

	Push(st, e);
	maze[xi][yi] = -1;

	while (!StackEmpty(st))
	{
		GetTop(st, e);
		i = e.i;
		j = e.j;
		di = e.di;
		if (i == xe && j == ye)  //找到出口
		{
			k = 0;

			while (!StackEmpty(st))
			{
				Pop(st, e);
				path[k++] = e;
			}

			while (k >= 1)
			{
				k--;
				printf("(%d,%d)", path[k].i, path[k].j);
			}

			DestroyStack(st);
			return true;
		}

		find = false;
		while (di < 4 && !find)
		{
			di++;
			switch (di)
			{
			case 0:i1 = i; j1 = j + 1; break;  //向右
			case 1:i1 = i + 1; j1 = j; break;  //向下
			case 2:i1 = i; j1 = j - 1; break;  //向左
			case 3:i1 = i - 1; j1 = j; break;  //向上
			}

			if (maze[i1][j1] == 0)
			{
				find = true;
			}
		}
		if (find)
		{
			st->data[st->top].di = di;
			e.i = i1;
			e.j = j1;
			e.di = -1;
			Push(st, e);
			maze[i1][j1] = -1;
		}
		else
		{
			Pop(st, e);
			maze[e.i][e, j] = 0;
		}
	}
	DestroyStack(st);
	return false;
}

int main()
{
	int n;
	scanf("%d", &n);

	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	if (!mgpath(1, 1, n-2, n-2))
		printf("NO\n");

	return 0;
}

实验代码（队列）

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define MaxSize 100

typedef struct
{
	int i, j;
	int pre;
}Box;

typedef struct
{
	Box data[MaxSize];
	int front, rear;
}QuType;

int maze[MaxSize][MaxSize];

void InitQueue(QuType*& q)  //初始化队列
{
	q = (QuType*)malloc(sizeof(QuType));
	q->front = q->rear = -1;
}

void DestroyQueue(QuType*& q)  //销毁队列
{
	free(q);
}

bool QueueEmpty(QuType* q)  //判断队列是否为空
{
	return (q->front == q->rear);
}

bool enQueue(QuType*& q, Box e)  //进队列
{
	if (q->rear == MaxSize - 1)
		return false;
	q->rear++;
	q->data[q->rear] = e;
	return true;
}

bool deQueue(QuType*& q, Box& e)  //出队列
{
	if (q->front == q->rear)
		return false;
	q->front++;
	e = q->data[q->front];
	return true;
}
void print(QuType* qu, int front)  //从队列qu中输出迷宫路径
{
	int k = front, j;

	do
	{
		j = k;
		k = qu->data[k].pre;
		qu->data[j].pre = -1;
	} while (k != 0);


	k = 0;
	while (k < MaxSize)
	{
		if (qu->data[k].pre == -1)
		{
			printf("(%d,%d)", qu->data[k].i, qu->data[k].j);
		}
		k++;
	}
}

bool mgpath(int xi, int yi, int xe, int ye)  //迷宫算法
{
	Box e;
	int i, j, di, i1, j1;
	QuType* qu;

	InitQueue(qu);
	e.i = xi;
	e.j = yi;
	e.pre = -1;

	enQueue(qu, e);
	maze[xi][yi] = -1;

	while (!QueueEmpty(qu))
	{
		deQueue(qu, e);
		i = e.i;
		j = e.j;
		if (i == xe && j == ye)
		{
			print(qu, qu->front);
			DestroyQueue(qu);
			return true;
		}

		for (di = 0; di < 4; di++)
		{
			switch (di)
			{
			case 0:i1 = i - 1; j1 = j; break;
			case 1:i1 = i; j1 = j + 1; break;
			case 2:i1 = i + 1; j1 = j; break;
			case 3:i1 = i; j1 = j - 1; break;
			}

			if (maze[i1][j1] == 0)
			{
				e.i = i1;
				e.j = j1;
				e.pre = qu->front;
				enQueue(qu, e);
				maze[i1][j1] = -1;
			}
		}
	}
	DestroyQueue(qu);
	return false;
}

int main()
{
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			scanf("%d", &maze[i][j]);
		}
	}

	if (!mgpath(1, 1, n - 2, n - 2))
		printf("NO\n");

	return 0;
}