8. Linear Transformations

8.1 Linear Requires

Keys:

1. A linear transformation T takes vectors v to vectors T(v). Linearity requires:

   \[T(cv +dw) = cT(v) + dT(w) \]

2. The input vectors v and outputs T(v) can be in \(R^n\) or matrix space or function space.

3. If A is m by n, \(T(x)=Ax\) is linear from the input space \(R^n\) to the output space \(R^m\).

4. The derivative \(T(f)=\frac{df}{dx}\) is linear.The integral \(T^+(f)=\int^x_0f(t)dt\) is its pseudoinverse.

   Derivative: \(1,x,x^2 \rightarrow 1,x\)

   \[u = a + bx + cx^2 \\ \Downarrow \\ Au = \left [ \begin{matrix} 0&1&0 \\ 0&0&2 \end{matrix} \right] \left [ \begin{matrix} a \\ b \\ c \end{matrix} \right] =\left [ \begin{matrix} b \\ 2c \end{matrix} \right] \\ \Downarrow \\ \frac{du}{dx} = b + 2cx \]

   Integration: \(1,x \rightarrow x,x^2\)

   \[\int^x_0(D+Ex)dx= Dx + \frac{1}{2}Ex^2 \\ \Downarrow \\ input \ \ v \ \ (D+Ex) \\ A^+v = \left[ \begin{matrix} 0&0 \\ 1&0 \\ 0&\frac{1}{2} \end{matrix} \right] \left[ \begin{matrix} D \\ E \end{matrix} \right] =\left[ \begin{matrix} 0 \\D \\ \frac{1}{2}E \end{matrix} \right] \\ \Downarrow \\ T^+(v) = Dx + \frac{1}{2}Ex^2 \]

5. The product ST of two linear transformations is still linear : \((ST)(v)=S(T(v))\)

6. Linear : rotated or stretched or other linear transformations.

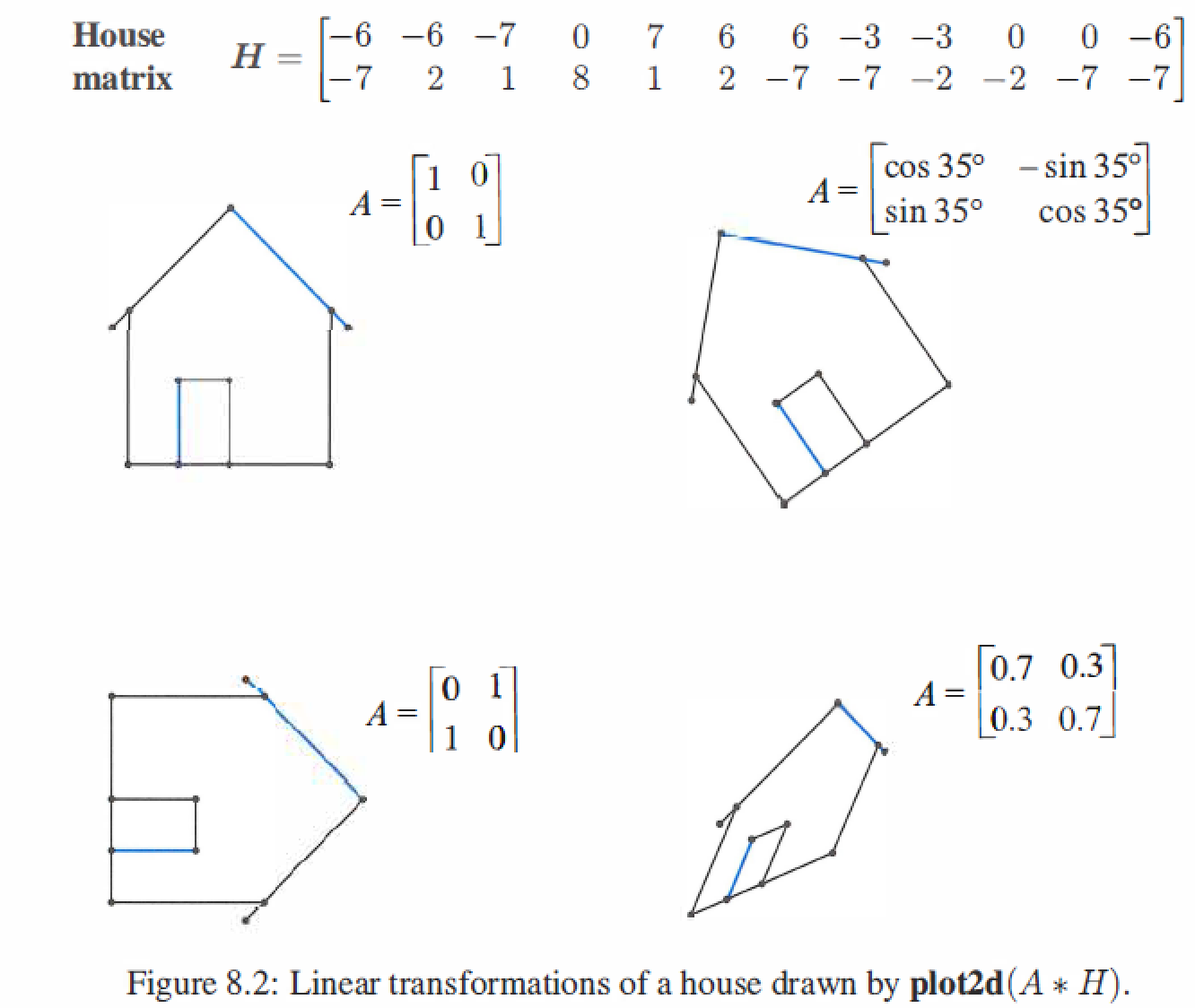
8.2 Matrix instead of Linear Transformation

We can assign a matrix A to instead of every linear transformation T.

For ordinary column vectors, the input v is in \(V=R^n\) and the output \(T(v)\) is in \(W=R^m\), The matrix A for this transformation will be m by n.Our choice of bases in V and W will decide A.

8.2.1 Change of Basis

if \(T(v) = v\) means T is the identiy transformation.

1. If input bases = output bases, then the matrix \(I\) will be choosed.

2. If input bases not equal to output bases, then we can construct new matrix \(B=W^{-1}V\).

   example:

   \[input \ \ basis \ \ [v_1 \ \ v_2] = \left [ \begin{matrix} 3&6 \\ 3&8 \end{matrix} \right] \\ output \ \ basis \ \ [w_1 \ \ w_2] = \left [ \begin{matrix} 3&0 \\ 1&2 \end{matrix} \right] \\ \Downarrow \\ v_1 = 1w_1 + 1w_2 \\ v_2 = 2w_1 + 3w_2 \\ \Downarrow \\ [w_1 \ \ w_2] [B] = [v_1 \ \ v_2] \\ \Downarrow \\ \left [ \begin{matrix} 3&0 \\ 1&2 \end{matrix} \right] \left [ \begin{matrix} 1&2 \\ 1&3 \end{matrix} \right] = \left [ \begin{matrix} 3&6 \\ 3&8 \end{matrix} \right] \]

   when the input basis is in the columns of V, and the output basis is in the columns of W, the change of basis matrix for \(T\) is \(B=W^{-1}V\).

   Suppose the same vector u is written in input basis of v's and output basis of w's:

   \[u=c_1v_1 + \cdots + c_nv_n \\ u=d_1w_1 + \cdots + d_nw_n \\ \left [ \begin{matrix} v_1 \cdots v_n \end{matrix} \right] \left [ \begin{matrix} c_1 \\ \vdots \\ c_n \end{matrix} \right] = \left [ \begin{matrix} w_1 \cdots w_n \end{matrix} \right] \left [ \begin{matrix} d_1 \\ \vdots \\ d_n \end{matrix} \right] \\ Vc=Wd \\ d = W^{-1}Vc = Bc \\ \]

   c is coordinates of input basis, d is coordinates of output basis.

8.2.2 Construction Matrix

Suppose T transforms the space V to space W. We choose a basis \(v_1,v_2,...,v_n\) for V and a basis \(w_1,w_2,...,w_n\) for W.

\[T(v_j) = combination \ \ of \ \ output \ \ basis \ \ vectors \\ =a_{1j}w_1 + \cdots + a_{mj}w_m \]

The \(a_{ij}\) are into A.

\[v = c_1 + c_2x + c_3x^2 + c_4x^3 \\ T(v) =\frac{dv}{dx} = 1c_2 + 2c_3x + 3c_4x^2 \\ Ac=\left[ \begin{matrix} 0&1&0&0 \\ 0&0&2&0\\ 0&0&0&3 \end{matrix} \right] \left[ \begin{matrix} c_1 \\ c_2 \\ c_3 \\ c_4 \end{matrix} \right] =\left[ \begin{matrix} c_2 \\ 2c_3 \\ 3c_4 \end{matrix} \right] \]

T takes the derivative, A is "derivative matrix".

8.2.3 Choosing the Best Bases

The same T is represented by different matrices when we choose different bases.

Perfect basis

Eigenvectors are the perfect basis vectors.They produce the eigenvalues matrix \(\Lambda = X^{-1}AX\)

Input basis = output basis

The new basis of b's is similar to A in the standard basis:

\[A_{b's \ \ to \ \ b's} = B^{-1}_{standard \ \ to \ \ b's} A_{standard} B^{-1}_{b's \ \ to \ \ strandard} \]

Different basis

Probably A is not symmetric or even square, we can choose the right singular vectors (\(v_1,...,v_n\)) as input basis and the left singular vectors(\(u_1,...,u_n\)) as output basis.

\[B_{out}^{-1}AB_{in} = U^{-1}AV=\Sigma \ \ (singular \ \ values) \]

\(\Sigma\) is "isometric" to A.

Definition : \(C=Q^{-1}_1AQ_{2}\) is isometric to A if \(Q_1\) and \(Q_2\) are orthogonal.

8.2.4 The Search of a Good Basis

Keys: fast and few basis.

1. $B_{in} = B_{out} = $ eigenvector matrix X . Then \(X^{-1}AX\)= eigenvalues in \(\Lambda\).
2. $B_{in} = V \ , \ B_{out} = U $ : singular vectors of A. Then \(U^{-1}AV\)= singular values in \(\Sigma\).
3. $B_{in} = B_{out} = $ generalized eigenvectors of A . Then \(B^{-1}AB\)= Jordan form \(J\).
4. $B_{in} = B_{out} = $ Fourier matrix F . Then \(Fx\) is a Discrete Fourier Transform of x.
5. The Fourier basis : \(1,sinx,cosx,sin2x,cos2x,...\)
6. The Legendre basis : \(1, x, x^2 - \frac{1}{3},x^3 - \frac{3}{5},...\)
7. The Chebyshev basis : \(1, x, 2x^2 - 1,4x^3 - 3x,...\)
8. The Wavelet basis.