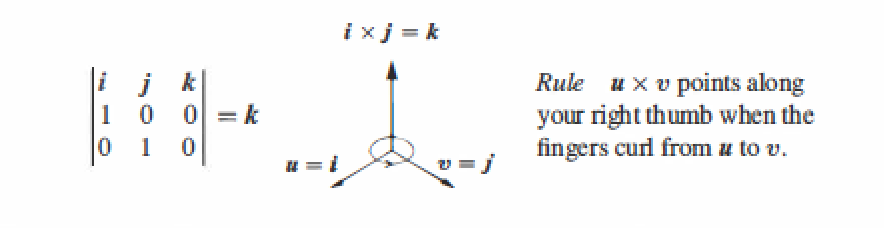5. Determinant

5.1 The Properties of Determinants

1. The determinant of the n by n identity matrix is 1 : \(det I = 1\).

2. The determinant changes sign when two rows are exchanged(sign reversal) : \(det P = \pm 1\) (det P = +1 for an even number of row exchange and det P = -1 for an odd number.)

3. The determinant is linear function of each row separately :

   • 3a : multiply row i for any number t det is multiplied by t : \(\left[ \begin{matrix} ta&tb \\ c&d \end{matrix} \right] = t\left| \begin{matrix} a&b \\ c&d \end{matrix} \right|\)
   • 3b: add row i of A to row i of A' then determinants add : \(\left[ \begin{matrix} a+a'&b+b' \\ c&d \end{matrix} \right] = \left| \begin{matrix} a&b \\ c&d \end{matrix} \right| + \left| \begin{matrix} a'&b' \\ c&d \end{matrix} \right|\)

   From rules 1-3 we will reach rules 4-10.

4. If two rows of A are equal, the det A = 0.

5. Subtracting a multiple of one row from another row leaves det A unchanged. ( eliminaton steps doesn't change determinant : det A = det D, without row exchanges.)

6. A matrix with a row of zeros has det A = 0.

7. If A is triangular then \(det A = a_{11}a_{22}...a_{nn}\)=product of diagnonal entries.

8. If A is singular then det A = 0. If A is invertible then \(det A \neq 0\).

9. The determinant of AB is det A times det B : \(|AB| = |A||B|\) .

10. The transpose \(A^T\) has the same determinant as A: \(det A^T = det A\).

    • A zero column will make the det A = 0.
    • Two equal columns will make the det A = 0.
    • If a column is multiplied by t, so is the determinant.

5.2 Three Formula for Determinant

The Pivot Formula

When elimination leads to \(A=LU\)， the pivots \(d_1,d_2,...,d_n\) are on the diagonal of the upper triangular U.

No row exchanges: \(det A = (det L)(det U)=(1)(d_1d_2...d_n)\)

Row exchanges: \((detP)(detA)= (detL)(detU)\) gives \(detA = \pm(d_1d_2...d_n)\) , odd leads to minus(-), even leads to plus(+)

The Big Formula

The big formula has n! terms.

\[det A = \sum(detP)a_{1\alpha}a_{1\beta}...a_{n\omega} \]

example:

\[\left| \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \\\end{matrix} \right| = \left| \begin{matrix} a_{11}&&\\ &a_{22}& \\ &&a_{33} \\\end{matrix} \right| + \left| \begin{matrix} &a_{12}&\\ &&a_{23} \\ a_{31}&& \\\end{matrix} \right| + \left| \begin{matrix} &&a_{13}\\ a_{21}&& \\ &a_{32}& \\\end{matrix} \right| +\\ \quad \quad \quad \quad \quad \quad \quad \quad \left| \begin{matrix} a_{11}&&\\ &&a_{23} \\ &a_{32}& \\\end{matrix} \right| + \left| \begin{matrix} &a_{12}&\\ a_{21}&& \\ &&a_{33} \\\end{matrix} \right| + \left| \begin{matrix} &&a_{13}\\ &a_{22}& \\ a_{31}&& \\\end{matrix} \right| + \\ \Downarrow \\ det A = a_{11}a_{22}a_{33}\left| \begin{matrix} 1&&\\ &1& \\ &&1\\\end{matrix} \right| + a_{12}a_{23}a_{31}\left| \begin{matrix} &1&\\ &&1 \\ 1&&\\\end{matrix} \right| + a_{13}a_{21}a_{32}\left| \begin{matrix} &&1\\ 1&& \\ &1&\\\end{matrix} \right| + \\ \quad \quad \quad a_{11}a_{23}a_{32}\left| \begin{matrix} 1&&\\ &&1 \\ &1&\\\end{matrix} \right| + a_{12}a_{21}a_{33}\left| \begin{matrix} &1&\\ 1&& \\ &&1\\\end{matrix} \right| + a_{13}a_{22}a_{31}\left| \begin{matrix} &&1\\ &1& \\ 1&&\\\end{matrix} \right| \\ \quad \quad \quad =a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} - a_{13}a_{22}a_{31} \]

The Cofactors Formula

The determinant is the dot product of any row i of A with its cofactors using other rows:

\[det A = a_{i1}C_{i1} + a_{i2}C_{i2} + ... + a_{in}C_{in} \]

Each cofactor \(C_{ij}\) (order n-1, without row i and column j) includes its correct sign:

\[C_{ij} = (-1)^{i + j} det M_{i+j} \]

example:

\[\left| \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \\\end{matrix} \right| = \left| \begin{matrix} a_{11}&&\\ &a_{22}&a_{23} \\ &a_{32}&a_{33} \\\end{matrix} \right| + \left| \begin{matrix} &a_{12}&\\ a_{21}&&a_{23} \\ a_{31}&&a_{33} \\\end{matrix} \right| + \left| \begin{matrix} &&a_{13}\\ a_{21}&a_{22}& \\ a_{31}&a_{32}& \\\end{matrix} \right| \]

\[C_{11} = a_{22}a_{33}-a_{23}a_{32} \\ C_{12} = -(a_{21}a_{33}-a_{23}a_{31}) \\ C_{13} = a_{21}a_{32}-a_{22}a_{31} \]

5.3 Inverse\ Cramer's Rule\ Volumn of box

Formula for \(A^{-1}\)

The i, j entry of \(A^{-1}\) is the cofactor \(C_{ji}\) divided by det A：

\[(A_{ij}^{-1}) = \frac{C_{ji}}{det A} \\ A^{-1} = \frac {C^T}{detA} \]

proof :

\[A^{-1} = \frac {C^T}{detA} \\ \Uparrow \\ AC^T = (detA)I \\ \Uparrow \\ \left[ \begin{matrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \\\end{matrix} \right] \left[ \begin{matrix} C_{11}&C_{21}&C_{31}\\ C_{12}&C_{22}&C_{32} \\ C_{13}&C_{23}&C_{33} \\\end{matrix} \right] = \left[ \begin{matrix} detA&0&0\\ 0&detA&0 \\ 0&0&detA \\\end{matrix} \right] \]

Cramer's Rule

If det A is not zero, Ax=b is solved by determinants:

\[x_1 = \frac{det B_1}{detA} , x_2 = \frac{det B_2}{detA}, \cdots, x_n = \frac{det B_n}{detA} \]

The matrix \(B_j\) has the jth column of A replaced by the vector b.

example:

\[Solve \quad Ax = (1,0,0) \\ det B_1 = \left| \begin{matrix} 1&a_{12}&a_{13}\\ 0&a_{22}&a_{23} \\ 0&a_{32}&a_{33} \\\end{matrix} \right| \\ det B_2 =\left| \begin{matrix} a_{11}&1&a_{13}\\ a_{21}&0&a_{23} \\ a_{31}&0&a_{33} \\\end{matrix} \right| \\ det B_3 =\left| \begin{matrix} a_{11}&a_{12}&1\\ a_{21}&a_{22}&0\\ a_{31}&a_{32}&0 \\\end{matrix} \right| \]

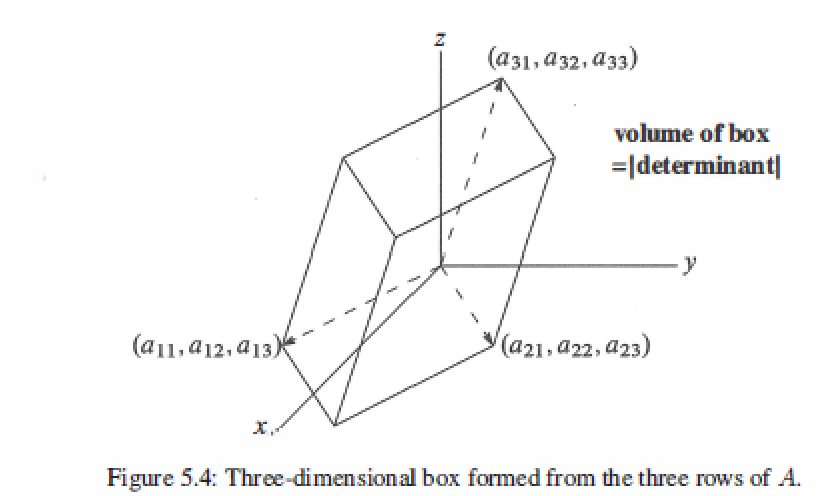
Volumn of box

The volume equals the absolute value of det A.

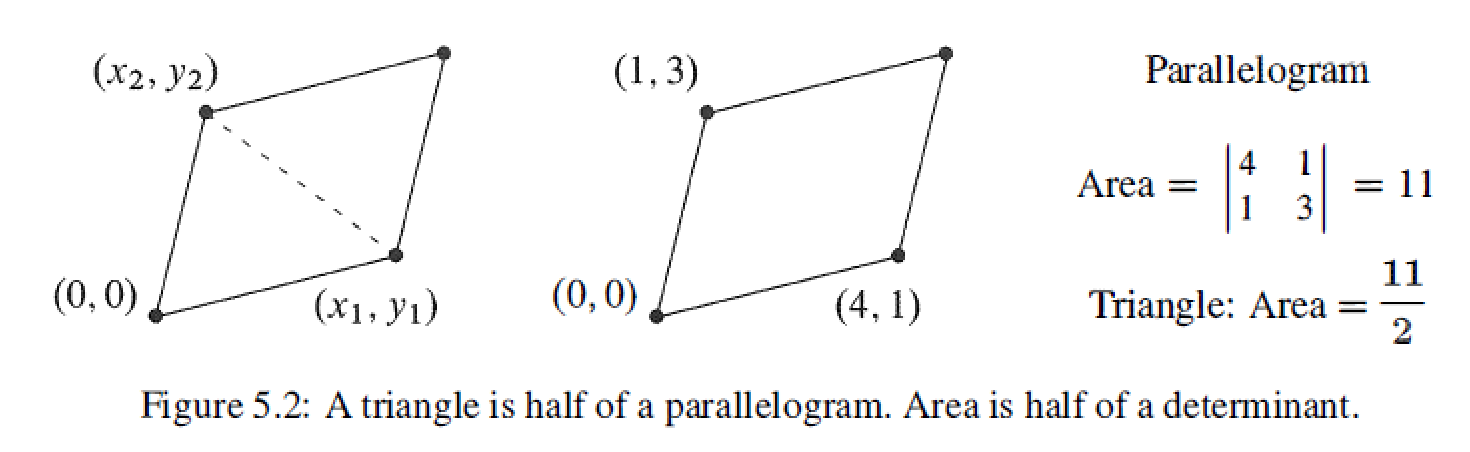
Area of Parallelogram and Triangle

Determinants are the best way to find area.

Area of Parallelogram : \(Area = Determinant\)

Area of Triangle: \(Area = Determinant / 2\)

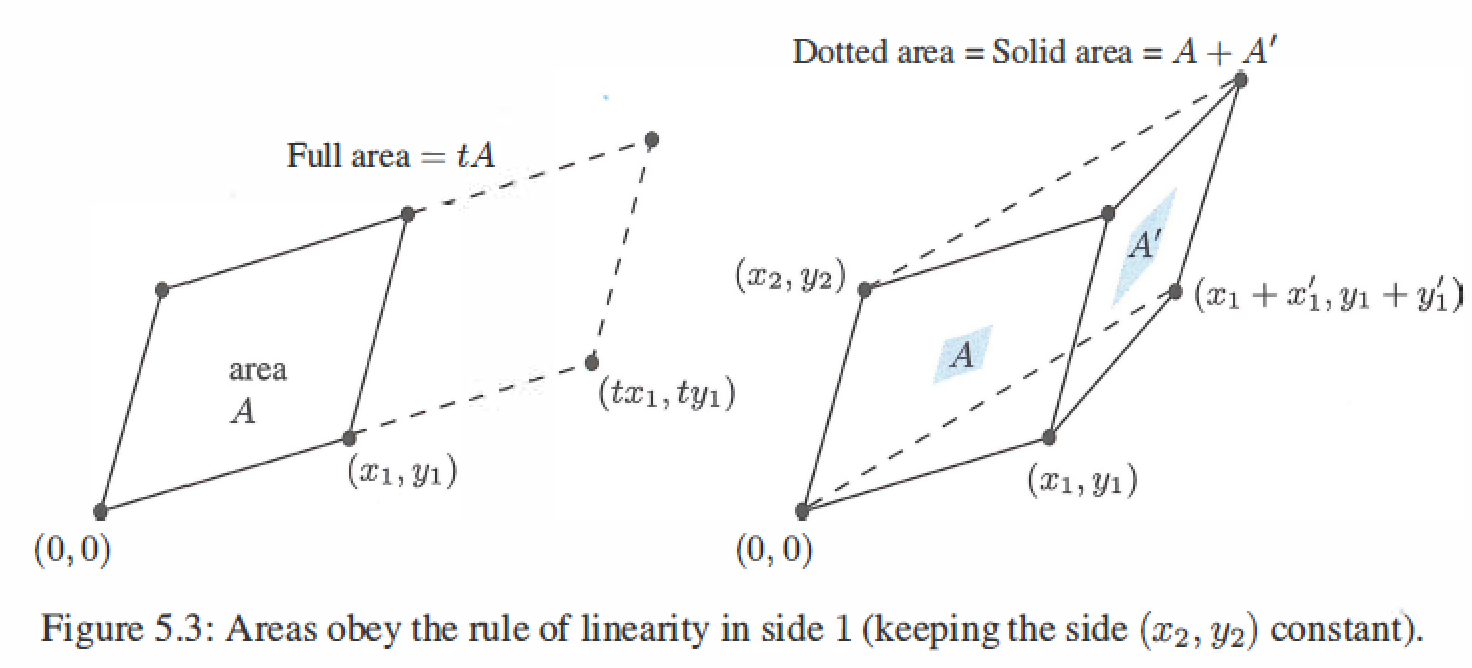
When an edge is stretched by a factor t, the volume is multiplied by t. (Rule 3a)

When edge 1 is added to edge 1'， the volume is the sum of the two original volumes.(Rule 3b)

5.4 Cross Product

The cross product of \(u=(u_1,u_2,u_3)\) and \(v=(v_1,v_2,v_3)\) is a vector.

\[u \times v = \left[ \begin{matrix} i&j&k \\ u_1&u_2&u_3 \\ v_1&v_2&v_3 \end{matrix} \right] = (u_2v_3-u_3v_2)i + (u_3v_1-u_1v_3)j +(u_1v_2-u_2v_1)k \]

The cross product is a vector with length \(||u|| \ \ ||v|| \ \ |sin\theta|\). Its direction is perpendicular to u and v.It points "up" or "down" by the right hand rule.

\[||u \times v|| =||u|| \ \ ||v||\ \ |sin\theta| \\ ( ||u \cdot v|| =||u|| \ \ ||v||\ \ |cos\theta| ) \]