3. Vector Spaces and Subspaces

3.1 Vector Spaces

The space \(R^n\) consists of all colunm vectors \(v\) with n components. We can add any vectors in \(R^n\) , and we can multiply any vector \(v\) by any scalar c , the result stays in the space \(R^n\).

examples:

columns between brackets : \(\left[ \begin{matrix} 4 \\ \pi \end{matrix} \right]\) is in \(R^2\)

commas and parentheses : (1,1,0,1,1) is in \(R^5\)

complex numbers spaces : \(\left[ \begin{matrix} 1 + i \\ 1-i \end{matrix} \right]\)

3.2 Subspaces

A subspace of a vector space is a set of vectors (including 0) that satisfies two requirements.

If \(v\) and \(w\) are vectors in the subspace and c is any scalar, then:

• rule 1 : \(v + w\) is in the subspace.
• rule 2 : \(cv\) is in the subspace.
• rule 1 + rule 2 : $cv + dw $ is in the subspace. (subspace is closed.)

Every subspace contains the zero vector.

Example: \(R^3\) subspaces

• The whole space \(R^3\) is a subspace (of itself)-- The largest one.
• Any lines through (0,0,0) -- L
• Any plane through (0,0,0) -- P
• The single vector (0,0,0) -- Z (zero vectors space--The littlest one)

3.3 Column Space

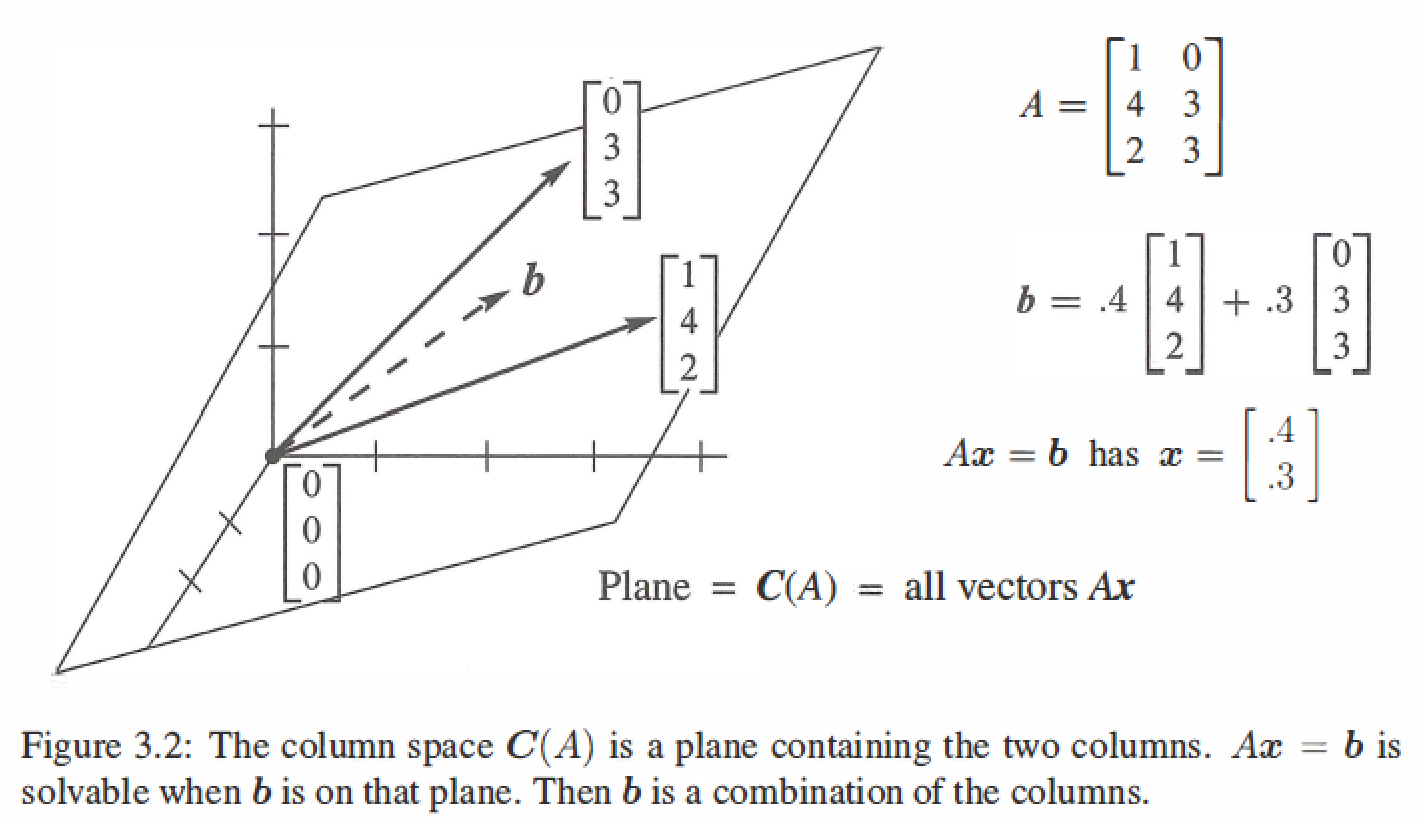
Ax =b , the column space of A is denoted by C(A) , C(A) contains not just the n columns of A, but all their combinations Ax，C(A) is a subspace of \(R^m\).

The system Ax=b is solvable if and only if b is in the column space of A.

\[C(A) = all \quad combinations \quad of \quad the \quad columns = all \quad vectors \quad Ax \]

example:

\[Ax = \left[ \begin{matrix} 1&0 \\ 4&3 \\ 2&3 \end{matrix}\right] \left[ \begin{matrix} x_1 \\ x_2 \end{matrix}\right] = x_1\left[ \begin{matrix} 1 \\ 4 \\ 2 \end{matrix}\right] + x_2\left[ \begin{matrix} 0 \\ 3 \\ 3 \end{matrix}\right] \]

3.4 The Nullspace : Ax=0 or Rx=0

Key notes:

• The nullspace N(A) in \(R^n\) contains all solutions x to \(Ax=0\). This includes x=0.
• Elimination (from A to U to R) does not change the nullspace : N(A)=N(U)=N(R).
• The reduced row echelon form R=rref(A) has all pivots = 1, with zeros above and below.
• If column j of R is free (no pivot), there is "special solution" to Ax=0 with \(x_j=1\).
• Number of pivots = number of nonzero rows in R = rank r . There are n-r free columns(variables\dimensions).
• Every matrix with m<n has nonzero solutions to Ax=0 in its nullspace.

Solution steps:

• reducing A to its row echelon form R.
• finding the special solutions to Ax=0. ( Ux = 0 or Rx = 0)
• N(A) = N(U) = N(R) = all combinations of special solutions.

\[A = \left [ \begin{matrix} p&p&f&p&f \\ \vdots&\vdots&\vdots&\vdots&\vdots \end{matrix}\right] \\ (3 \ \ pivot \ \ columns \ \ p ，2 \ \ free \ \ columns \ \ f) \\ step \ \ 1 \Downarrow \\ R = \left [ \begin{matrix} 1&0&a&0&c \\ 0&1&b&0&d \\ 0&0&0&1&e \\ 0&0&0&0&0 \end{matrix}\right] \\ (I \ \ in \ \ pivot \ \ columns ，F \ \ in \ \ free \ \ columns, 3 \ \ pivots: rank=3 ) \\ step \ \ 2 \Downarrow \\ s_1 =\left[ \begin{matrix} -a \\ -b \\ 1 \\ 0 \\ 0 \end{matrix}\right] \ \ s_2 =\left[ \begin{matrix} -c \\ -d \\ 0 \\ -e \\ 1 \end{matrix}\right] \\ step \ \ 3 \Downarrow \\ N(A) = N(U) = N(R) = all \ \ combinations \ \ of \ \ s_1 \ \ and \ \ s_2. \]

3.5 The Complete solutions : Ax=b or Rx = d

Key notes:

• Complete solution to Ax=b : x = (one particular solution \(x_p\)) + (any \(x_n\) in the nullspace).
• Elimination on [A b] leads to [R d]. Then Ax=b is equivalent to Rx=d.
• Ax = b and Rx=d are solvable only when all zero rows of R have zeros in d.
• When Rx=d is solvable, one very particular solution \(x_p\) has all free variables equal to zero.
• A has full rank r=n when its nullspace N(A) = zero vector : no free variables.
• A has full row rank r = m when its column space C(A) is \(R^m\) : Ax=b is always solvable.

Solution steps:

• Produce the augmented matrix [A b]
• Get Elimination form [R d]
• Set free variables = 0, and get a particular solution -- \(x_p\)
• Set free variables = 1 or 0，and get n - r special solutions -- \(x_n\)
• Complete solution: \(x = x_p + x_n\)

example:

\[Ax = b \\ \Downarrow \\ \left [ \begin{matrix} 1&3&0&2 \\ 0&0&1&4 \\ 1&3&1&6 \end{matrix}\right] \left [ \begin{matrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{matrix}\right] = \left [ \begin{matrix} 1 \\ 6 \\ 7 \end{matrix}\right] \\ \Downarrow \\ [A \ \ b] = \left [ \begin{matrix} 1&3&0&2&1 \\ 0&0&1&4&6 \\ 1&3&1&6&7 \end{matrix}\right] \\ \Downarrow \\ [R \ \ d] = \left [ \begin{matrix} 1&3&0&2&1 \\ 0&0&1&4&6 \\ 0&0&0&0&0 \end{matrix}\right] \\ \Downarrow \\ Pivot \ \ variables(x_1, x_3) = 1, 6 \\ Free \ \ variables (x_2, x_4) = 0, 0 \\ Solution \ \ x_p = (1, 0, 6, 0) \\ \Downarrow \\ Free \ \ variables (x_2, x_4) = 1 \ \ or \ \ 0 \\ s_1 = [-3, 1, 0, 0] \\ s_2 = [-2, 0, -4, 1] \\ x_n =c\left [ \begin{matrix} -3 \\ 1 \\ 0 \\ 0 \end{matrix}\right] + d\left [ \begin{matrix} -2 \\ 0 \\ -4 \\ 1 \end{matrix}\right] \\ \Downarrow \\ x = x_p + x_n = \left [ \begin{matrix} 1 \\ 0 \\ 6 \\ 0 \end{matrix}\right] + c\left [ \begin{matrix} -3 \\ 1 \\ 0 \\ 0 \end{matrix}\right] + d\left [ \begin{matrix} -2 \\ 0 \\ -4 \\ 1 \end{matrix}\right] \]

The four possibilities for linear equations depend on the rank k :

• r = m = n , square and invertible, \(R = [I]\)，Ax = b has 1 solution (unkowns=equations)
• r = m < n, short and wide, \(R = [I \ \ F]\)，Ax = b has infinite solutions (unkowns > equations)
• r = n < m，Tall and thin，\(R = \left [ \begin{matrix} I \\ F\end{matrix}\right]\), Ax = b 0 or 1 solutions (unkonwns < equations)
• r < n and r < m，not full rank，\(R = \left [ \begin{matrix} I&F \\ 0&0 \end{matrix}\right]\), Ax=b has 0 or infinite solutions

3.6 Independence, Basis and Dimension

Independent

• Independent columns of A : The only solution to Ax=0 is x=0, the nullspace is Z.
• Independent vectors : The only zero combination \(c_1v_1 + c_2v_2 + ... + c_kv_k = 0\) has all c's = 0.
• A matrix with m<n has dependent columns : At least n-m free variables/special solutions.

Basis

A basis for a vector space is a sequence of vectors with two properties:

• The basis vectors are linearly independent.
• They span the space.
  • The rows are in \(R^n\) spanning the row space.
  • The columns are in \(R^m\) spanning the column space.

Every vector \(v\) in the space is a combination of the basis vectors, because they span the space, and there is only one way to write \(v\) as a combination of the basis vectors.

The pivot columns of A are a basis for its column space. The pivot rows of A are a basis for its row space. So are the pivot rows of its echelon form R.

• a basis of \(C(A)\) = pivots columns of A.
• a basis of \(C(A^T)\) = pivots rows of A.

example:

\[A = \left[ \begin{matrix} 2&4 \\ 3&6 \end{matrix}\right] \quad reduces \quad to \quad R = \left[ \begin{matrix} 1&2 \\ 0&0 \end{matrix}\right] \]

The column spaces of A and R are different and their bases are different.

Column 1 of R is the pivot column, which alone is a basis for C(R): \(\left[ \begin{matrix} 1 \\ 0\end{matrix} \right]\)

Column 1 of A is the pivot column, which alone is a basis for C(A): \(\left[ \begin{matrix} 2 \\ 3\end{matrix} \right]\)

Row 1 of R is the pivot row, which alone is a basis for \(C(R^T)=C(A^T)\): \(\left[ \begin{matrix} 1&2 \end{matrix} \right]\)

Dimension

The dimension of a space is the number of vectors in every basis.

Bases for Matrix Spaces and Function Spaces

Matrix spaces:

• The vector space M contains all n by n matrices, its dimension is \(n^2\).
• The dimension of the subspace of upper triangular matrices is \(1/2n^2 + 1/2 n\).
• The dimension of the subspace of diagonal matrices is n.
• The dimension of the subspace of symmetric matrices if \(1/2n^2 + 1/2 n\).

example:

One basis

\[A_1, A_2,A_3,A_4 = \left[ \begin{matrix} 1&0 \\ 0&0 \end{matrix}\right], \left[ \begin{matrix} 0&1 \\ 0&0 \end{matrix}\right], \left[ \begin{matrix} 0&0 \\ 1&0 \end{matrix}\right], \left[ \begin{matrix} 0&0 \\ 0&1 \end{matrix}\right] \]

Every A combines the basis matrices

\[A = c_1A_1 + c_2A_2 +c_3A_3 +c_4A_4 = \left[ \begin{matrix} c_1&c_2 \\ c_3&c_4 \end{matrix}\right] \]

Function spaces:

• \(y''=0\) is solved by any linear function \(y = cx + d\)，the space bases has x and 1.
• \(y'' = -y\) is solved by any combination \(y= csinx + dcosx\), the space bases has \(sinx\) and \(cosx\).
• \(y'' = y\) is solved by any combination \(y=ce^x + de^{-x}\)，the space bases has \(e^x\) and \(e^{-x}\).

3.7 Dimensions of the Four Subspaces

Keys notes:

• The column space is \(C(A)\)，a subspace of \(R^m\), has a dimensions r，\(r=pivot \ \ columns\)

• The row space is \(C(A^T)\)，a subspace of \(R^n\), has a dimensions r, \(r=pivot \ \ rows\)

• The nullspace is \(N(A)\)，a subspace of \(R^n\), has a dimensions \(n-r\), numbers of free variables

• The left nullspace is \(N(A^T)\)，a subspace of \(R^m\), has a dimensions \(m-r\), numbers of free rows

example : Ax = b

\[A = \left[ \begin{matrix} -1&1&0&0 \\ -1&0&1&0 \\ 0&-1&1&0 \\ 0&-1&0&1 \\ 0&0&-1&1 \end{matrix}\right] \quad reduces \ \ to \ \ R = \left[ \begin{matrix} 1&0&0&-1 \\ 0&1&0&-1 \\ 0&0&1&-1 \\ 0&0&0&0 \\ 0&0&0&0 \end{matrix}\right] \]

1. The column space \(C(A)\) : r = 3 independent columns, a basis is the columns 1,2,3 of A.
2. The row space \(C(A^T)\) : r = 3 independent rows, a basis is the rows 1,2,4 of A or R. (\(P_{34}EA=R\))
3. The nullspace N(A) : Set b = 0, N(A) = N(R)，n - r = 4 - 3 = 1 free variables, x = (1, 1, 1, 1) is the basis for N(A).
4. The nullspace \(N(A^T)\) :
   • m-r = 5 - 3 = 2 dimensions;
   • Solve \(A^Ty = 0\)，combinations of the rows give zero, get special solutions \(y_1 = (1, -1, 1, 0, 0), y_2 = (0,0,-1,1,-1)\)，a basis of \(N(A^T)\) is \(y_1, y_2\).
   • If EA=R， the last m-r rows of R are a basis for the left nullspace of A.

3.8 Rank One Matrices

• Every rank one matrix is one column times one row : \(A=uv^T\)

  \[\left[ \begin{matrix} 2&3&7&8 \\ 2a&3a&7a&8a \\ 2b&3b&7b&8b \end{matrix} \right] = \left[ \begin{matrix} 1 \\ a \\ b \end{matrix} \right] \left[ \begin{matrix} 2&3&7&8 \end{matrix} \right] = uv^T \]

• Every rank r matrix is a sum of r rank one matrices.

  \[A =\left[ \begin{matrix} &&& \\ u_1&u_2&u_3 \\ &&& \end{matrix} \right] \left[ \begin{matrix} v_1^T \\ v_2^T \\ zero \ \ row \end{matrix} \right] = u_1v_1^T + u_2v_2^T\\ rank_A = rank1 + rank1 \]