1. Vectors and Linear Combinations
1.1 Vectors
We have n separate numbers \(v_1、v_2、v_3,...,v_n\),that produces a n-dimensional vector \(v\),and \(v\) is represented by an arrow.
Two-dimensional vector :\(v = \left[\begin{matrix} v_1 \\ v_2 \end{matrix}\right]\) and \(w = \left[\begin{matrix} w_1 \\ w_2 \end{matrix}\right]\)
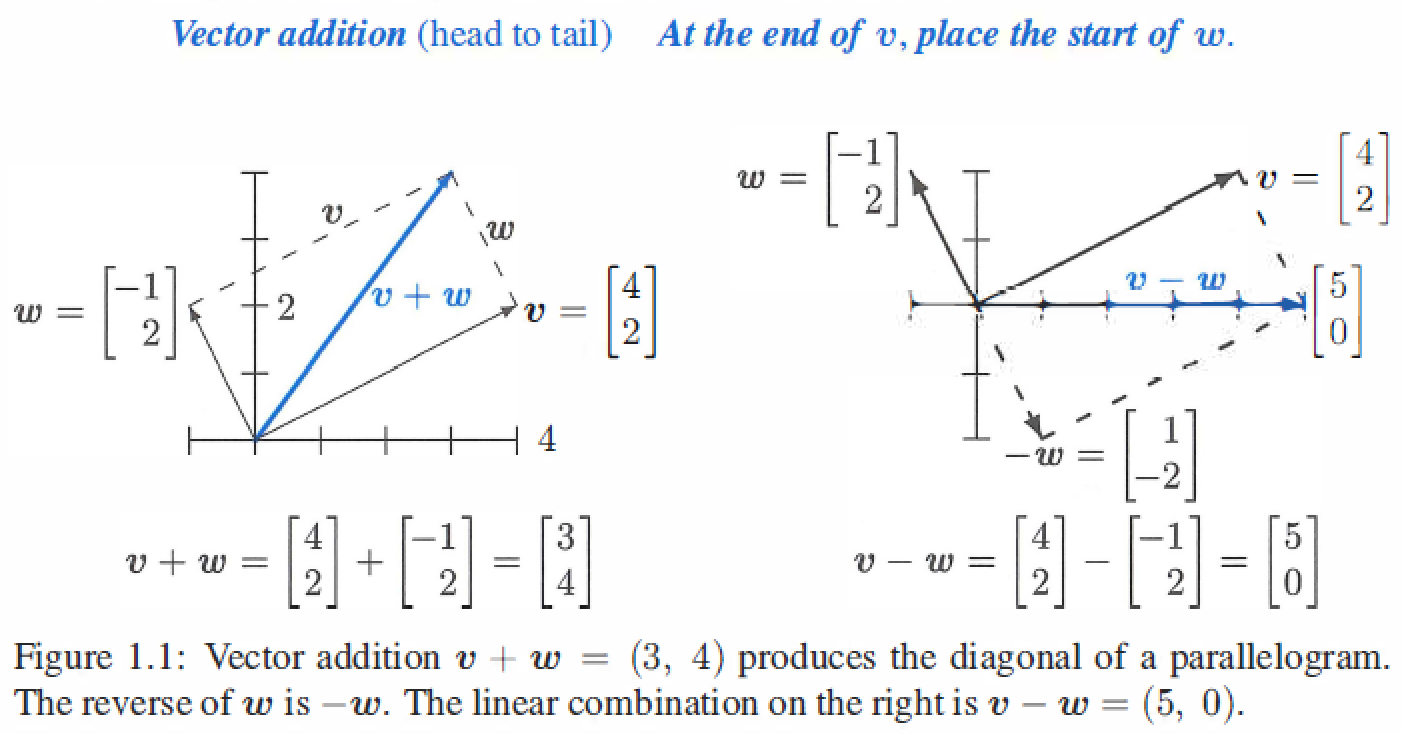
- Vector Addition : \(v + w = \left[\begin{matrix} v_1 + w_1 \\ v_2 + w_2\end{matrix}\right]\)
- Scalar Multiplication : \(cv = \left[\begin{matrix} cv_1 \\ cv_2 \end{matrix}\right]\),c is scalar.
1.2 Linear Combinations
Multiply \(v\) by \(c\) and multiply \(w\) by \(d\),the sum of \(cv\) and \(dw\) is a linear combination : \(cv + dw\).
We can visualize \(v + w\) using arrows,for example:
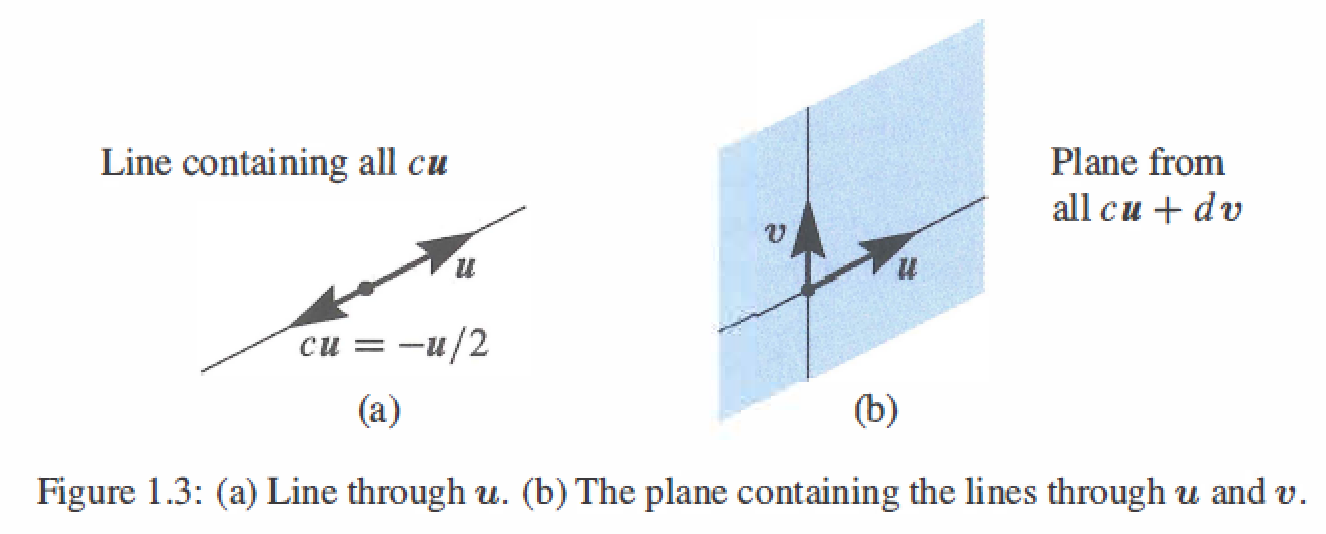
The combinations can fill Line、Plane 、or 3-dimensional space:
- The combinations \(cu\) fill a line through origin.
- The combinations \(cu + dv\) fill a plane throught origin
- The combinations \(cu + dv +ew\) fill three-dimensional space throught origin.
1.3 Lengths and Dot Products
Dot Product/ Inner Product: \(v \cdot w = v_1w_1 + v_2w_2\),where $v = (v_1, v_2) $ and \(w=(w_1, w_2)\) ,the dot product \(w \cdot v\) equals \(v \cdot w\)
Length : \(||v|| = \sqrt{v \cdot v} = (v_1^2 + v_2^2 + v_3^2 +...+ v_n^2)^{1/2}\)
Unit vector : \(u = v /||v||\) is a unit vector in the same direction as \(v\),length =1
Perpendicular vector : \(v \cdot w = 0\)
Cosine Formula : if \(v\) and \(w\) are nonzero vectors then \(\frac{v \cdot w}{||v|| \ ||w||} = cos \theta\) , \(\theta\) is the angle between \(v\) and \(w\)
Schwarz Inequality : \(|v \cdot w| \leq ||v|| \ ||w||\)
Triangel Inequality : \(||v + w|| \leq ||v|| + ||w||\)
1.4 Matrices
1、\(A = \left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}\right]\) is a 3 by 2 matrix : m=2 rows and n=2 columns
2、$Ax = b $ is a linear combination of the columns A
3、 Combination of the vectors : \(Ax = x_1\left[ \begin{matrix} 1 \\ -1 \\ 0 \end{matrix} \right] + x_2\left[ \begin{matrix} 0 \\ 1 \\ -1 \end{matrix} \right] + x_3\left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2 \end{matrix} \right]\)
4、Matrix times Vector : $Ax = \left[ \begin{matrix} 1&0&0\ -1&1&0 \ 0&-1&1 \end{matrix} \right] \left[ \begin{matrix} x_1\ x_2 \ x_3 \end{matrix} \right]= \left[ \begin{matrix} x_1 \ x_2-x_1 \ x_3-x_2 \end{matrix} \right] $
5、Linear Equation : Ax = b --> \(\begin{matrix} x_1 = b_1 \\ -x_1 + x_2 = b_2 \\ -x_2 + x_3 = b_3 \end{matrix}\)
6、Inverse Solution : \(x = A^{-1}b\) -- > \(\begin{matrix} x_1 = b_1 \\ x_2 = b_1 + b_2 \\ x_3 =b_1 + b_2 + b_3 \end{matrix}\), when A is an invertible matrix
7、Independent columns : Ax = 0 has one solution, A is an invertible matrix, the column vectors of A are independent. (example: \(u,v,w\) are independent,No combination except \(0u + 0v + 0w = 0\) gives \(b=0\))
8、Dependent columns : Cx = 0 has many solutions, C is a singular matrix, the column vectors of C are dependent. (example: \(u,v,w^*\) are dependent,other combinations like \(au + cv + dw^*\) gives \(b=0\))




