Numpy通用函数及向量化计算
Python(Cpython)对于较大数组的循环操作会比较慢,因为Python的动态性和解释性,在做每次循环时,必须做数据类型的检查和函数的调度。
Numpy为很多类型的操作提供了非常方便的、静态类型的、可编译程序的接口,称为向量操作,通过通用函数实现,使数组中的数据运算执行效率更快。
In [3]: import numpy as np
In [4]: arr = np.arange(10)
In [5]: arr
Out[5]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#arr数组中的每个元素都执行一次sqrt函数(开方)
In [6]: np.sqrt(arr)
Out[6]:
array([0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
#arr数组中的每个元素都执行一次exp函数(指数)
In [7]: np.exp(arr)
Out[7]:
array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
2.98095799e+03, 8.10308393e+03])
In [8]: x = np.random.randn(10)
In [9]: y = np.random.randn(10)
In [10]: x
Out[10]:
array([-0.82366085, -0.03255978, 2.50626464, 0.33865153, 0.43386721,
-0.74543163, -2.64879417, -1.07827856, -0.29578612, 1.47010253])
In [11]: y
Out[11]:
array([-0.29522902, 0.37414633, -1.05189119, -1.17025433, 1.03573013,
-0.20660426, 1.06281893, -0.49384468, -1.8739977 , 1.25588708])
#maximum对x和y数组相应位置的元素逐个比较,并输出值较大的
In [12]: np.maximum(x,y)
Out[12]:
array([-0.29522902, 0.37414633, 2.50626464, 0.33865153, 1.03573013,
-0.20660426, 1.06281893, -0.49384468, -0.29578612, 1.47010253])
In [13]: arr = np.random.randn(7)*5
In [14]: arr
Out[14]:
array([ 4.98279157, -1.27419373, 4.16720012, -10.48931255,
4.49418926, 0.735708 , 0.07716139])
#modf函数分别获取数组中每个元素的整数和小数
In [15]: reminder,whole_part = np.modf(arr)
In [16]: reminder
Out[16]:
array([ 0.98279157, -0.27419373, 0.16720012, -0.48931255, 0.49418926,
0.735708 , 0.07716139])
In [17]: whole_part
Out[17]: array([ 4., -1., 4., -10., 4., 0., 0.])
In [18]: arr
Out[18]:
array([ 4.98279157, -1.27419373, 4.16720012, -10.48931255,
4.49418926, 0.735708 , 0.07716139])
In [19]: np.sqrt(arr)
Out[19]:
array([2.23221674, nan, 2.04137212, nan, 2.1199503 ,
0.85773423, 0.27777938])
In [20]: arr
Out[20]:
array([ 4.98279157, -1.27419373, 4.16720012, -10.48931255,
4.49418926, 0.735708 , 0.07716139])
#sqrt(x, /[, out, where, casting, order, …]),x表示输入的数组,out表示存放的位置
#np.sqrt(arr,arr)表示对arr数组开方,并把结果存入原来arr数组中,则原来arr数组中的数就会发生变化
In [21]: np.sqrt(arr,arr)
Out[21]:
array([2.23221674, nan, 2.04137212, nan, 2.1199503 ,
0.85773423, 0.27777938])
In [22]: arr
Out[22]:
array([2.23221674, nan, 2.04137212, nan, 2.1199503 ,
0.85773423, 0.27777938])
向量化计算
数组的向量化计算可以同时处理数组需要循环才能完成的任务,效率比循环更高。
In [23]: points = np.arange(-5,5,0.01)
#meshgrid创建一个规则的数值网格,xs为x轴网格线,ys为y轴网格线
In [24]: xs, ys = np.meshgrid(points,points)
In [25]: xs
Out[25]:
array([[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
...,
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99],
[-5. , -4.99, -4.98, ..., 4.97, 4.98, 4.99]])
In [26]: ys
Out[26]:
array([[-5. , -5. , -5. , ..., -5. , -5. , -5. ],
[-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
[-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
...,
[ 4.97, 4.97, 4.97, ..., 4.97, 4.97, 4.97],
[ 4.98, 4.98, 4.98, ..., 4.98, 4.98, 4.98],
[ 4.99, 4.99, 4.99, ..., 4.99, 4.99, 4.99]])
In [27]: z = np.sqrt(xs ** 2 + ys ** 2)
In [28]: z
Out[28]:
array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
7.06400028],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
...,
[7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
7.04279774],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568]])
In [29]: import matplotlib.pyplot as plt
#imshow画图形
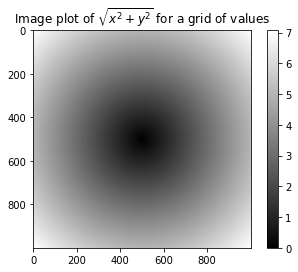
In [30]: plt.imshow(z,cmap=plt.cm.gray);plt.colorbar()
Out[30]: <matplotlib.colorbar.Colorbar at 0x20351df58c8>
#title画图形标题
In [31]: plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
Out[31]: Text(0.5, 1, 'Image plot of $\\sqrt{x^2 + y^2}$ for a grid of values')
数组条件逻辑运算
numpy.where(condition,x,y)是一个向量化的三元表达式(x if condition==True else y)。
In [32]: xarr = np.array([1.1,1.2,1.3,1.4,1.5])
In [33]: yarr = np.array([2.1,2.2,2.3,2.4,2.5])
In [34]: cond = np.array([True, False, True, True, False])
#通过列表表达式+for\zip实现
In [35]: result = [(x if c else y) for x,y,c in zip(xarr, yarr, cond)]
In [36]: result
Out[36]: [1.1, 2.2, 1.3, 1.4, 2.5]
#np.where()直接实现上面列表表达式的逻辑
In [38]: result = np.where(cond,xarr,yarr)
In [39]: result
Out[39]: array([1.1, 2.2, 1.3, 1.4, 2.5])
In [40]: arr = np.random.randn(4,4)
In [41]: arr
Out[41]:
array([[ 1.59209108, -0.4086942 , 0.4407095 , 1.15434273],
[-0.4809145 , -1.22923284, -1.15852576, 1.29476618],
[ 0.15114022, -0.78129023, -0.51957822, -0.39520662],
[ 0.13733152, 1.55691611, -2.31871851, -0.26706437]])
In [42]: arr > 0
Out[42]:
array([[ True, False, True, True],
[False, False, False, True],
[ True, False, False, False],
[ True, True, False, False]])
In [43]: np.where(arr >0 ,1,0)
Out[43]:
array([[1, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 0, 0],
[1, 1, 0, 0]])
In [44]: np.where(arr >0,1,arr)
Out[44]:
array([[ 1. , -0.4086942 , 1. , 1. ],
[-0.4809145 , -1.22923284, -1.15852576, 1. ],
[ 1. , -0.78129023, -0.51957822, -0.39520662],
[ 1. , 1. , -2.31871851, -0.26706437]])
数学和统计方法
In [45]: arr = np.random.randn(5,4)
In [46]: arr
Out[46]:
array([[ 0.46511456, -0.75494472, -0.11214598, 0.89848079],
[-1.42332991, 0.337035 , -0.22018627, -0.33635835],
[-2.9157174 , -2.04946947, -1.46504217, -2.1854843 ],
[ 0.91287505, 0.20984805, 0.58966139, 1.18746111],
[-0.08732871, -1.36381031, -0.10451817, -0.90514938]])
#mean()求平均值,默认求全部元素的平均值,加入参数axis=0表示沿0轴求平均值,axis=1表示沿1轴求平均值
In [47]: arr.mean()
Out[47]: -0.46615045863486665
In [48]: np.mean(arr)
Out[48]: -0.46615045863486665
In [49]: arr.mean(axis=1)
Out[49]: array([ 0.12412616, -0.41070988, -2.15392833, 0.7249614 , -0.61520164])
In [50]: arr.mean(axis=0)
Out[50]: array([-0.60967728, -0.72426829, -0.26244624, -0.26821002])
#sum()求和,默认求全部元素的和,加入参数axis=0表示沿0轴求和,axis=1表示沿1轴求和
In [51]: arr.sum()
Out[51]: -9.323009172697333
In [52]: arr.sum(axis=1)
Out[52]: array([ 0.49650465, -1.64283952, -8.61571333, 2.89984559, -2.46080656])
In [53]: arr.sum(axis=0)
Out[53]: array([-3.04838641, -3.62134144, -1.31223119, -1.34105012])
In [54]: arr = np.array([[0,1,2],[3,4,5],[6,7,8]])
In [55]: arr
Out[55]:
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
#cumsum()求累计和,默认求全部元素的累计和,加入参数axis=0表示沿0轴求累计和,axis=1表示沿1轴求累计和
In [56]: arr.cumsum(axis=0)
Out[56]:
array([[ 0, 1, 2],
[ 3, 5, 7],
[ 9, 12, 15]], dtype=int32)
In [57]: arr.cumsum(axis=1)
Out[57]:
array([[ 0, 1, 3],
[ 3, 7, 12],
[ 6, 13, 21]], dtype=int32)
#cumprod()求累积,默认求全部元素的累积,加入参数axis=0表示沿0轴求累积,axis=1表示沿1轴求累积
In [58]: arr.cumprod(axis=0)
Out[58]:
array([[ 0, 1, 2],
[ 0, 4, 10],
[ 0, 28, 80]], dtype=int32)
In [59]: arr.cumprod(axis=1)
Out[59]:
array([[ 0, 0, 0],
[ 3, 12, 60],
[ 6, 42, 336]], dtype=int32)
布尔运算方法
In [60]: arr = np.random.randn(100)
In [61]: arr
Out[61]:
array([ 1.97279219, 1.56694167, -0.55398407, 0.15938761, -1.90688396,
0.12198921, 0.36810009, 0.23750045, -0.45220466, 0.02077729,
-0.65948605, 0.57359337, -0.66764519, -0.14284721, 0.19014932,
0.91210127, -1.23914144, 0.53690069, -0.522095 , -0.99396945,
-0.25311752, 0.89034877, -0.8311114 , -0.16252583, -0.27005923,
-0.55920499, 1.73472904, -0.01973033, 0.92402808, -0.16614446,
0.2736938 , -0.28145616, -0.09546974, 0.530437 , 0.39995646,
-0.85350062, -0.51831624, -1.69345104, -0.64163665, -0.39480043,
1.38246309, 1.06339284, 1.18405756, 2.03400374, -0.42610591,
0.35906461, -0.55486399, 0.70110865, -0.78864601, -0.29954069,
1.94746481, -0.52377169, 0.24632122, 0.62128442, -0.5238096 ,
0.56636735, -0.00591474, 1.66648525, 1.5606595 , -0.86025501,
1.13356963, -1.55629377, -0.91746296, -0.69410977, 1.96398699,
0.15773424, 0.1475058 , -0.48767326, 0.65743225, -2.43297787,
-0.14665574, -1.16361457, -0.9753315 , -0.17658007, 0.07366705,
-0.34816566, -0.19779013, -0.26078629, 0.64939326, 0.68780731,
0.2898325 , -0.29745762, 1.35564769, -1.71548972, -1.309609 ,
0.33786133, -0.00713603, -2.01114545, -0.41214938, 0.20788337,
-0.70684644, -3.2529954 , 0.69005349, 1.5902472 , -0.54671729,
1.58654547, 0.03035015, 0.62181632, 0.14706786, -0.90948163])
#用arr > 0的条件判断,满足的元素相加
In [62]: (arr > 0 ).sum()
Out[62]: 47
In [63]: bools = np.array([False,False,True,False])
#any()数组中有一个True,则返回True
In [65]: bools.any()
Out[65]: True
#all()数组中所有的元素为True才返回True
In [66]: bools.all()
Out[66]: False
数组排列
sort()排列后直接替换原来的数组。
In [67]: arr = np.random.randn(6)
In [68]: arr
Out[68]:
array([-0.8710231 , 0.48971206, -0.65277359, -0.09909771, 0.45533796,
-0.02159873])
#sort()元素排列后直接替换原来的数组
In [69]: arr.sort()
In [70]: arr
Out[70]:
array([-0.8710231 , -0.65277359, -0.09909771, -0.02159873, 0.45533796,
0.48971206])
In [71]: arr = np.random.randn(5,3)
In [72]: arr
Out[72]:
array([[-0.10113188, -0.21734814, -0.76523088],
[-0.46665726, -0.25147201, -1.09096503],
[ 0.71719542, 0.21011708, 0.09206453],
[-0.22847625, 0.26928708, -0.3253391 ],
[ 1.3526748 , -1.61463912, -0.19217378]])
#沿1轴排序
In [73]: arr.sort(1)
In [74]: arr
Out[74]:
array([[-0.76523088, -0.21734814, -0.10113188],
[-1.09096503, -0.46665726, -0.25147201],
[ 0.09206453, 0.21011708, 0.71719542],
[-0.3253391 , -0.22847625, 0.26928708],
[-1.61463912, -0.19217378, 1.3526748 ]])
唯一性计算
np.unique()返回唯一并且排好序的数组。
In [75]: names = np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])
#提取names数组中的唯一元素,并排好序返回
In [76]: np.unique(names)
Out[76]: array(['Bob', 'Joe', 'Will'], dtype='<U4')
In [77]: ints = np.array([3,3,3,2,2,1,1,4,4])
In [78]: np.unique(ints)
Out[78]: array([1, 2, 3, 4])
In [79]: values = np.array([6,0,0,3,2,5,6])
#np.in1d(x,y)判断x中的元素是否包含在y中,是返回True,否返回False
In [80]: np.in1d(values,[2,3,6])
Out[80]: array([ True, False, False, True, True, False, True])





