并查集
并查集从名字上来看就是 合并 和 查找 的 集合。对于一个全集 \(U\) 来说,并查集就是将 \(U\) 划分为几个不相交的子集,并对这些子集中的元素进行管理,主要实现下面两个功能:
查找: 给定一个元素,问这个元素属于哪一个集合?
合并: 给定两个元素(它们所属的集合不同)或给定两个集合,将这两个不相交的集合合并。
考虑暴力做法:
例如这几个集合{1,2,3},{4,5},{6};如果需要对其中的元素进行查找和集合合并,我们可能会这样想:
首先将这 3 个集合存起来,在 C++ 中可以使用 STL 中的 set 容器,C 语言中使用多维数组存储。
对于查找操作:如果我们要查找某个元素属于哪个集合,需要把所有集合都检查一遍
对于合并操作:如果将一个集合的元素与另一个集合合并,势必要将一个集合的所有元素复制一遍到另一个集合
上述算法的时间复杂度太大,每个集合的存储空间使用也是动态变化的
基本思想:
每个集合用一颗树来表示,如果两个元素属于同一集合,那么一个元素就指向另一个元素,也就说每个节点存储它的父节点编号。
当查找某个元素属于哪个集合时,从当前的节点递归的向上查找直到树根,树根的编号就是整个集合的编号。
我们用 f[x] 表示 x 的父节点。最先开始每个元素属于自己本身所在的集合:f[x] = x
-
如何判断树根?对于树根来说,它的父节点没有改变
if(f[x] == x) -
如何求 x 的集合编号?不断的向上查询直到遇到树根就停止
while(f[x] != x) x = f[x]; -
如何合并两个不相交集合?只需要改变其中一个集合的根节点的父节点编号就行
fx为 x 所在集合的编号,fy为 y 所在集合的编号,且fx !=fy,合并:f[fx] = fy
例题
模板题
M a b:将编号 a b 的两个数所在的集合合并,如果已经在同一集合则忽略
Q a b:询问编号为 a b 的两个数是否在同一个集合中
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
int f[N];
int Find(int x){
return f[x] == x ? x : (f[x] = Find(f[x]));
}
int main()
{
int n, m, a, b;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++ i)
f[i] = i;
char op[2];
while(m--)
{
scanf("%s%d%d", op, &a, &b);
int fa = Find(a), fb = Find(b);
if(op[0] == 'M'){
if(fa != fb){
f[fa] = fb;
}
}
else{
printf("%s\n", fa == fb ? "Yes" : "No");
}
}
return 0;
}
食物链
AcWing 240. 食物链 - AcWing / 1182 -- 食物链 (poj.org)
有三类动物 \(A\),\(B\),\(C\);\(A\) 吃 \(B\),\(B\) 吃 \(C\),\(C\) 吃 \(A\) ;现在有 \(N\) 个动物,以 \(1\sim N\) 编号
1 X Y 表示 \(X\) 和 \(Y\) 是同类
2 X Y 表示 \(X\) 吃 \(Y\)
现在依次说出 \(K\) 句话,如果后面的话与前面某些真的话冲突则为假话,如果有 \(X\) 吃 \(X\) 则为假话,如果有 \(X\) 或 \(Y\) 比 \(N\) 大则为假话;现要求计算假话的总数
思路
假设 X 吃 Y 则,X 与 Y 之间的距离为d[x] = 1
X 被 Y 则,X 与 Y 之间的距离为d[x] = 2
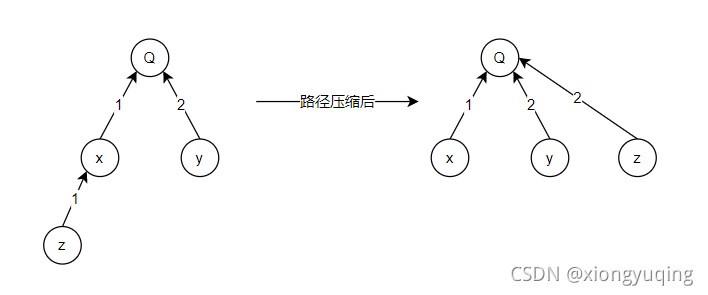
如果 x 吃 Q,y 被 Q 吃,z 吃 x。
在路径压缩后,z 的父节点发生了变化,那么d[z] 应该怎么更新呢?
我们观察到如果 z 吃 x,x 吃 Q,那么 z 就被 Q 吃,如果中间经历了很多边,那么我们发现每 3 个是一个循环,它会回到原来所属的种类
更新值等于当前节点到根节点路径距离的权值和模 3
那么可以画出下面的图:
判断真假算法:fx 为 X 的根节点,fy 为 Y 的根节点
-
X 和 Y 是同类
-
X 和 Y 属于同一个集合(
fx == fy为真),可以根据前面的说法提前得出 X 和 Y 的关系;(d[x] - d[y])%3 != 0说明不是同类,是假话,否则为真
-
X 和 Y 不属于同一个集合:集合合并:
f[fx] = fy- 现在要构造
d[fx]使得 X 和 Y 是同类,那么需要满足到根节点的距离相同: (d[x] + d[fx])%3 = d[y]%3\(\Rightarrow\)d[fx] = (d[y] - d[x])%3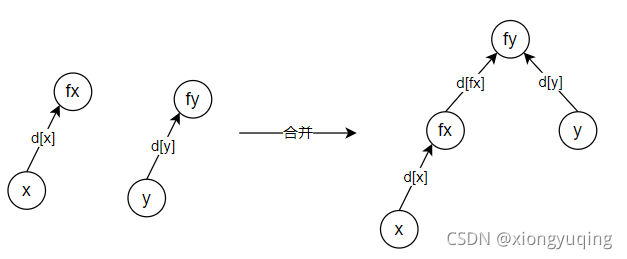
- 现在要构造
-
-
X 吃 Y
- X 和 Y 属于同一个集合(
fx == fy为真),可以根据前面的说法提前得出 X 和 Y 的关系- 根据上面的分析,我们发现如果 X 吃 Y,则
d[x]比d[y]始终大 1 - 那么如果
(d[x] - d[y] - 1)%3 != 0说明 X 不吃 Y,是假话,否则为真
- 根据上面的分析,我们发现如果 X 吃 Y,则
- X 和 Y 不属于同一个集合:集合合并:
f[fx] = fy- 现在要构造
d[fx]使得 X 吃 Y ,那么需要满足到根节点的距离 : (d[x] + d[fx] - 1)%3 = d[y]%3\(\Rightarrow\)d[fx] = (d[y] + 1 - d[x])%3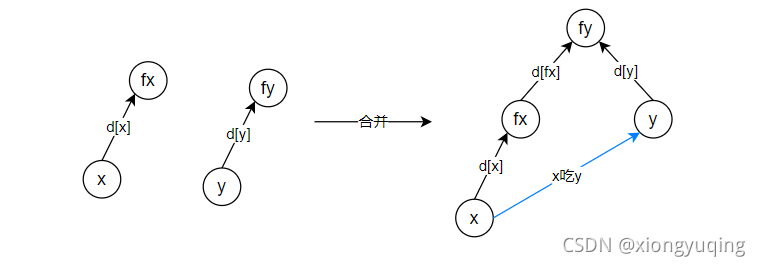
- 现在要构造
- X 和 Y 属于同一个集合(
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e4 + 5;
int f[N], d[N];
int Find(int x)
{
if(f[x] != x)
{
int u = Find(f[x]);
d[x] += d[f[x]];
f[x] = u;
}
return f[x];
}
int main()
{
int n, k;
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; ++ i) f[i] = i;
int m, x, y, ans = 0;
while(k--)
{
scanf("%d%d%d", &m, &x, &y);
if(x > n || y > n) ++ ans;
else if(m == 1)
{
int fx = Find(x), fy = Find(y);
if(fx == fy && (d[x] - d[y]) % 3) ++ ans;
else if(fx != fy)
{
f[fx] = fy;
d[fx] = d[y] - d[x];
}
}
else
{
int fx = Find(x), fy = Find(y);
if(fx == fy && (d[x] - d[y] - 1) % 3) ++ ans;
else if(fx != fy)
{
f[fx] = fy;
d[fx] = d[y] + 1 - d[x];
}
}
}
printf("%d", ans);
return 0;
}
本文来自博客园,作者:xiongyuqing,转载请注明原文链接:https://www.cnblogs.com/xiongyuqing/p/15234802.html


 对于一个全集 $U$ 来说,并查集就是将 $U$ 划分为几个不相交的子集,并对这些子集中的元素进行管理
对于一个全集 $U$ 来说,并查集就是将 $U$ 划分为几个不相交的子集,并对这些子集中的元素进行管理

