KMP基础

KMP算法用于模板串 \(P\) 与模式串 \(S\) 匹配过程中的算法优化

例如

模式串 S 为 ababa

模板串 P 为 aba

寻找 S 与 P完全匹配的下标，下标从 0 开始

那么答案是 0 和 2

---

思考暴力做法，对于模式串 S 中的每一个位置与 P 相匹配，如果有一个匹配不上，那么 S 向后挪动一位，P 从头开始与 S 匹配，复杂度 \(O(nm)\)

for(int i = 0; i < n; ++ i)
{
    int k = i;
    for(int j = 0; j < m; ++ j)
    {
        if(s[k] == p[j]) ++ k;
        else break;
    }
    if(k - i + 1 == m) cout << i << " ";
}

---

KMP 算法的优化方向：当匹配错误时，P 不从头开始重新与 S 匹配，而是利用之前的信息，向后跳转到新的匹配点，P 中每个位置的新匹配点的下标称作 next 数组。next 数组的实际意义是最大相同前后缀的长度。

匹配过程

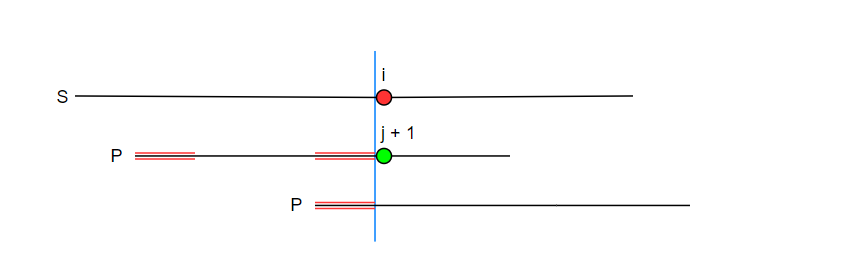
下图中字符串 P 的 j + 1 个字符和字符串 S 的第 i 个字符不匹配，那么此时 P 从红色前缀后面开始匹配而不是像暴力做法从头开始，减小了时间复杂度。红色部分就是 1 到 j 这段字符串相同的前后缀。为什么可以跳转呢？因为后缀部分和 S 已经匹配过了且相同，那么与后缀相同部分的前缀也就和这部分的 S 字符相同

例如，模式串ababa 和 模板串 aba 匹配

ababa
aba
匹配成功，答案：0
寻找下一个完全匹配的位置
由于aba的前缀a和后缀a相同所以向后跳转到a
ababa
  aba
匹配成功：答案：2

求模板串 P 的 next 数组？

考虑实际意义：相同前后缀的长度

类似 S 和 P 匹配的过程，如果 P 和 P 自己匹配，

那么就相当于被当作模式串的 P 后缀和当作模板串的 P 的前缀进行匹配，

当前已匹配的模板串的长度就是最大相同前后缀的长度

例如求 aba 的 next 数组

首先是 next[0] = 0
下标 i 从 1 开始
aba
 aba
b 和 a 不匹配，于是 j = 0 向后跳转 j = next[0] = 0，于是 next[1] = j = 0
下标 i 等于 2
aba
  aba
a 和 a 匹配，于是 j = 0, j ++ => j = 1，于是 next[2] = j = 1

例题

831. KMP字符串 - AcWing题库

注意这里代码的下标从 1 开始

#include <iostream>
using namespace std;

const int N = 1e5 + 5;
const int M = 1e6 + 5;
char p[N], s[M];
int ne[N];

int main()
{
    int n, m;
    cin >> n >> p + 1 >> m >> s + 1;
    // 求 next 数组
    for(int i = 2, j = 0; i <= n; ++ i)
    {
        while(j && p[i] != p[j + 1]) j = ne[j];
        if(p[i] == p[j + 1]) ++ j;
        ne[i] = j;
    }
    // 匹配
    for(int i = 1, j = 0; i <= m; ++ i)
    {
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j + 1]) ++j;
        if(j == n)
        {
            j = ne[j];
            cout << i - n << " ";
        }
    }
    return 0;
}