图解 二叉树的四种遍历

图解 二叉树的四种遍历

 

LeetCode 题目中，二叉树的遍历方式是最基本，也是最重要的一类题目，我们将从「前序」、「中序」、「后序」、「层序」四种遍历方式出发，总结他们的递归和迭代解法。

题目说明

这里是 4 道相关题目：

1. 144.二叉树的前序遍历
2. 94. 二叉树的中序遍历
3. 145. 二叉树的后序遍历
4. 102. 二叉树的层序遍历

二叉树及遍历方式

要解决这四道题目，最基本的前提是要了解什么是二叉树，以及二叉树的遍历方式。如果你已经有所了解，则可以直接查看下一节的内容。

首先，二叉树是一种「数据结构」，详细的介绍可以参考力扣的「探索」卡片来进行学习。简单来说，就是一个包含节点，以及它的左右孩子的一种数据结构。

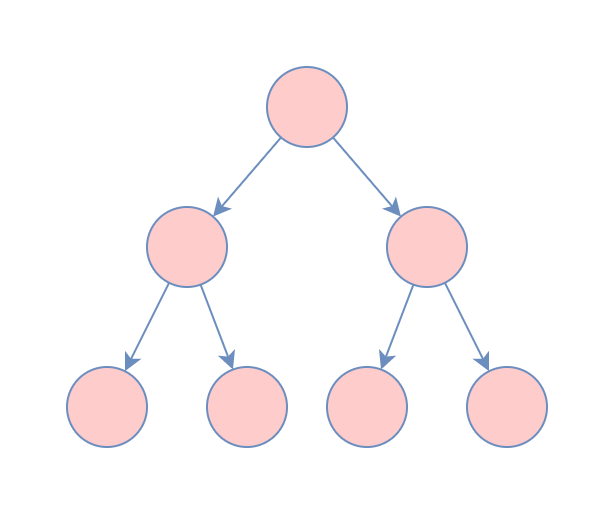
如果对每一个节点进行编号，你会用什么方式去遍历每个节点呢？

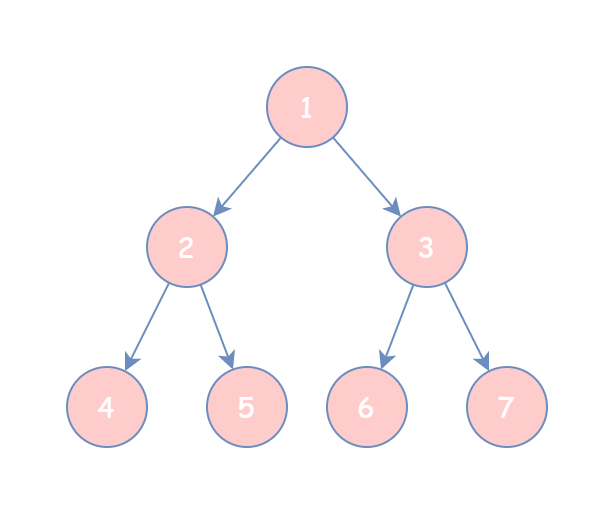
如果你按照 根节点 -> 左孩子 -> 右孩子 的方式遍历，即「先序遍历」，每次先遍历根节点，遍历结果为 1 2 4 5 3 6 7；

同理，如果你按照 左孩子 -> 根节点 -> 右孩子 的方式遍历，即「中序序遍历」，遍历结果为 4 2 5 1 6 3 7；

如果你按照 左孩子 -> 右孩子 -> 根节点 的方式遍历，即「后序序遍历」，遍历结果为 4 5 2 6 7 3 1；

最后，层次遍历就是按照每一层从左向右的方式进行遍历，遍历结果为 1 2 3 4 5 6 7。

题目解析

这四道题目描述是相似的，就是给定一个二叉树，让我们使用一个数组来返回遍历结果，首先来看递归解法。

递归解法

由于层次遍历的递归解法不是主流，因此只介绍前三种的递归解法。它们的模板相对比较固定，一般都会新增一个 dfs 函数：

对于前序、中序和后序遍历，只需将递归函数里的 res.append(root.val) 放在不同位置即可，然后调用这个递归函数就可以了，代码完全一样。

1. 前序遍历

2. 中序遍历

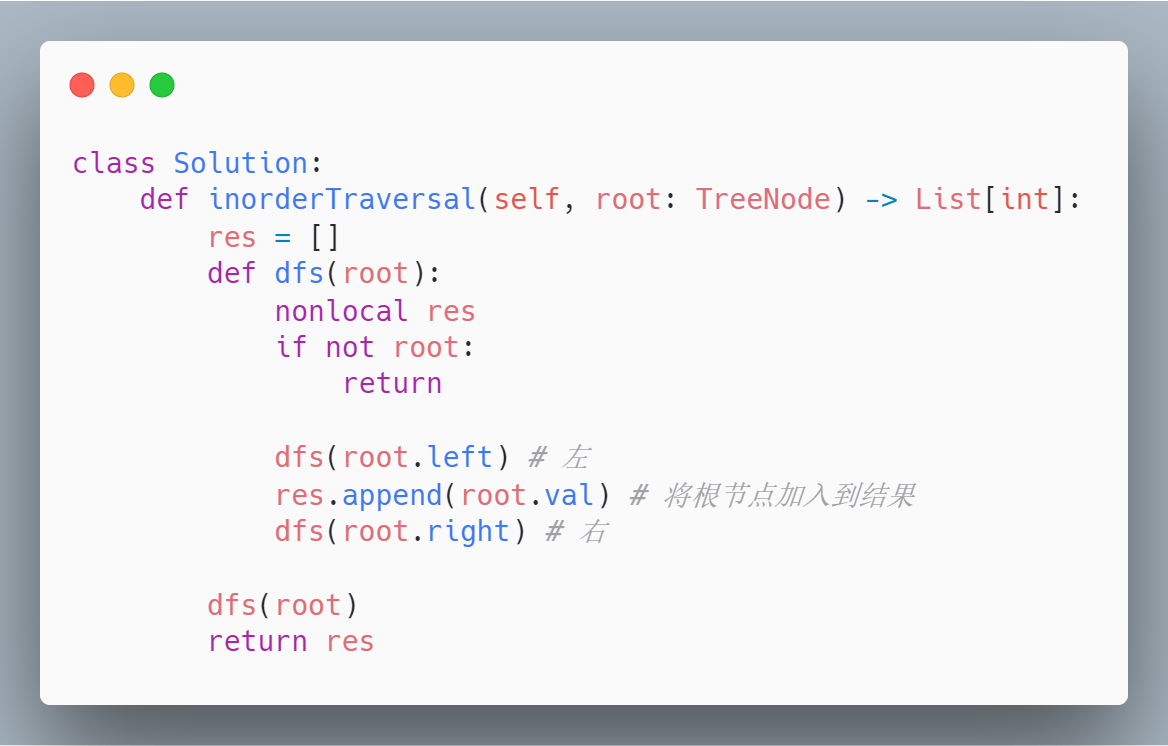
3. 后序遍历

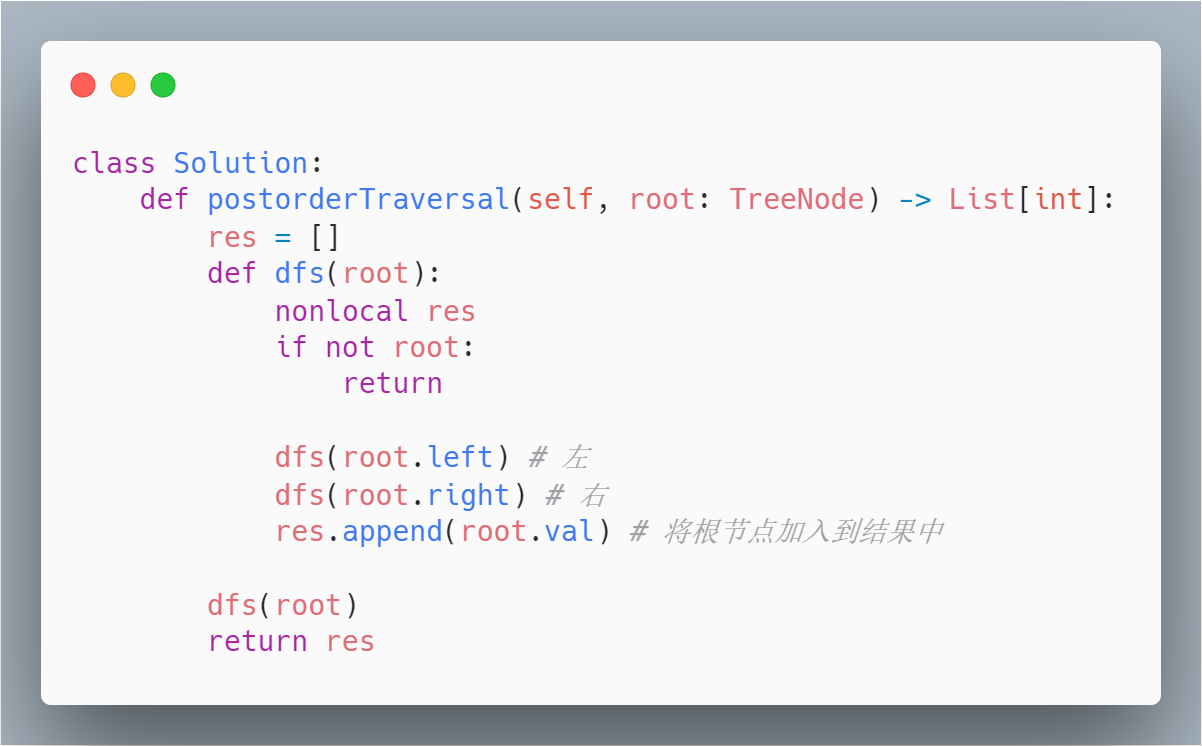
一样的代码，稍微调用一下位置就可以，如此固定的套路，使得只掌握递归解法并不足以令面试官信服。

因此我们有必要再掌握迭代解法，同时也会加深我们对数据结构的理解。

1. 二叉树的前序遍历

LeetCode 题目： 144.二叉树的前序遍历

常规解法

我们使用栈来进行迭代，过程如下：

• 初始化栈，并将根节点入栈；
• 当栈不为空时：
  • 弹出栈顶元素 node，并将值添加到结果中；
  • 如果 node 的右子树非空，将右子树入栈；
  • 如果 node 的左子树非空，将左子树入栈；

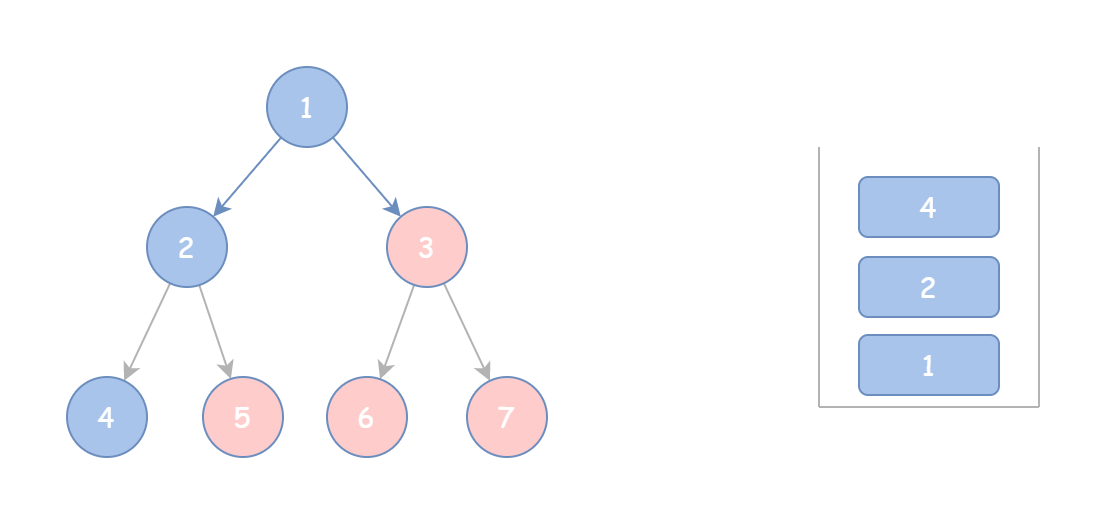
由于栈是“先进后出”的顺序，所以入栈时先将右子树入栈，这样使得前序遍历结果为 “根->左->右”的顺序。

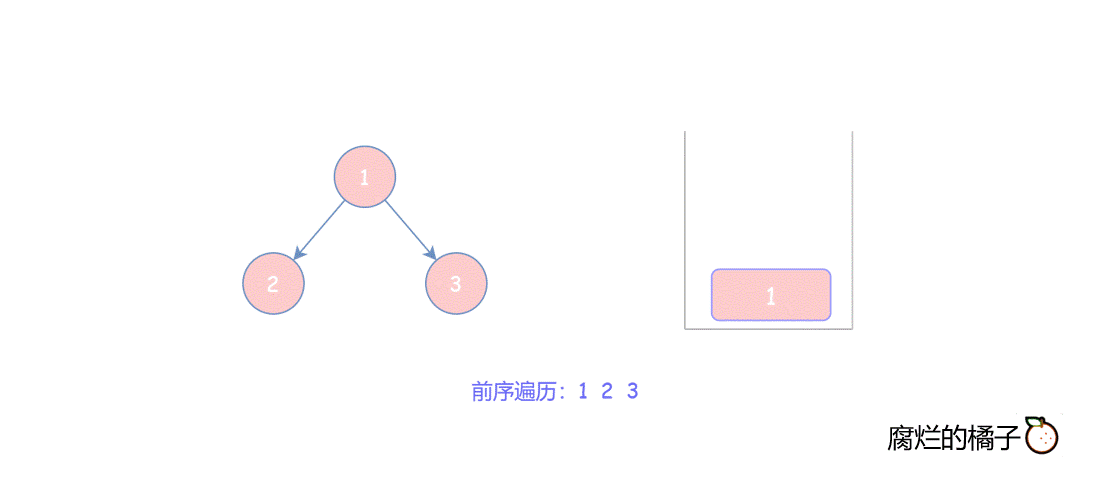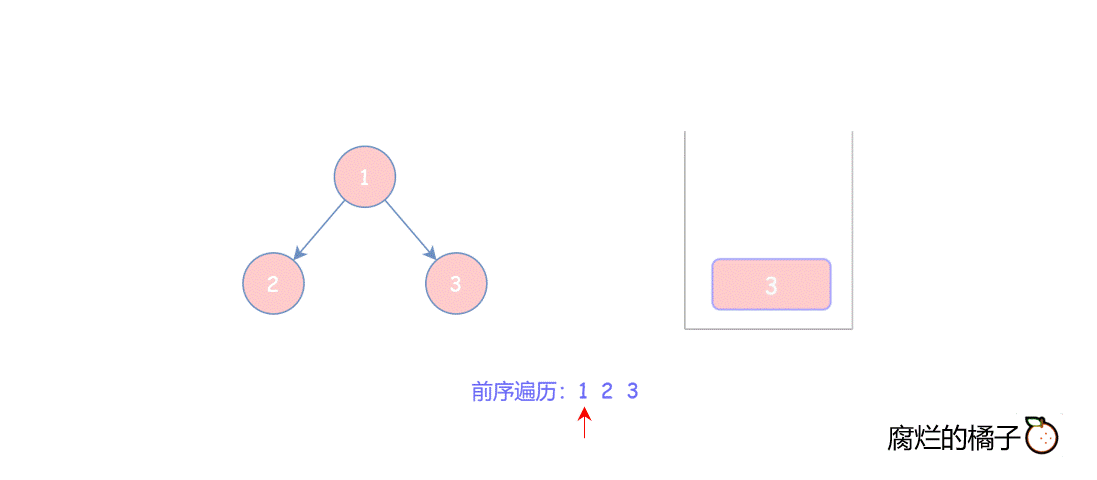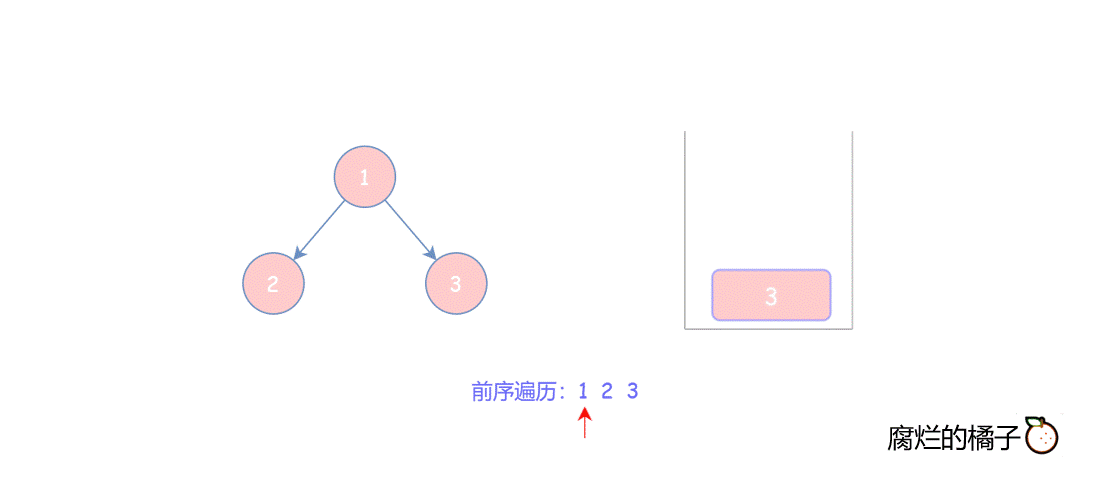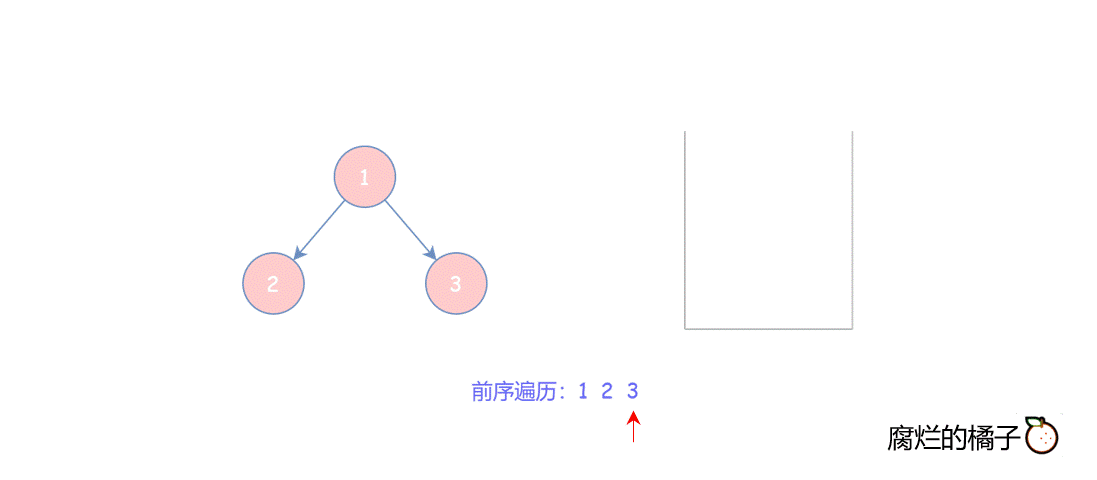
参考代码如下：

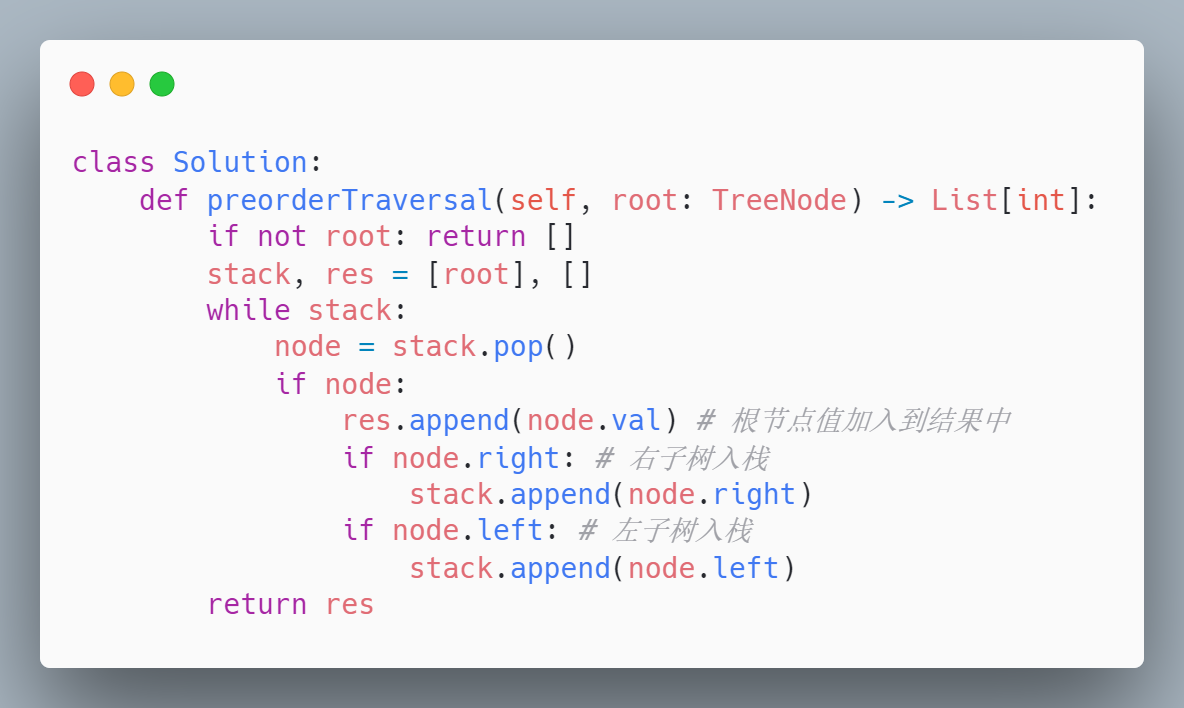
模板解法

当然，你也可以直接启动“僵尸”模式，套用迭代的模板来一波“真香操作”。

模板解法的思路稍有不同，它先将根节点 cur 和所有的左孩子入栈并加入结果中，直至 cur 为空，用一个 while 循环实现：

然后，每弹出一个栈顶元素 tmp，就到达它的右孩子，再将这个节点当作 cur 重新按上面的步骤来一遍，直至栈为空。这里又需要一个 while 循环。

参考代码如下：

2. 二叉树的中序遍历

LeetCode 题目：94. 二叉树的中序遍历

模板解法

和前序遍历的代码完全相同，只是在出栈的时候才将节点 tmp 的值加入到结果中。

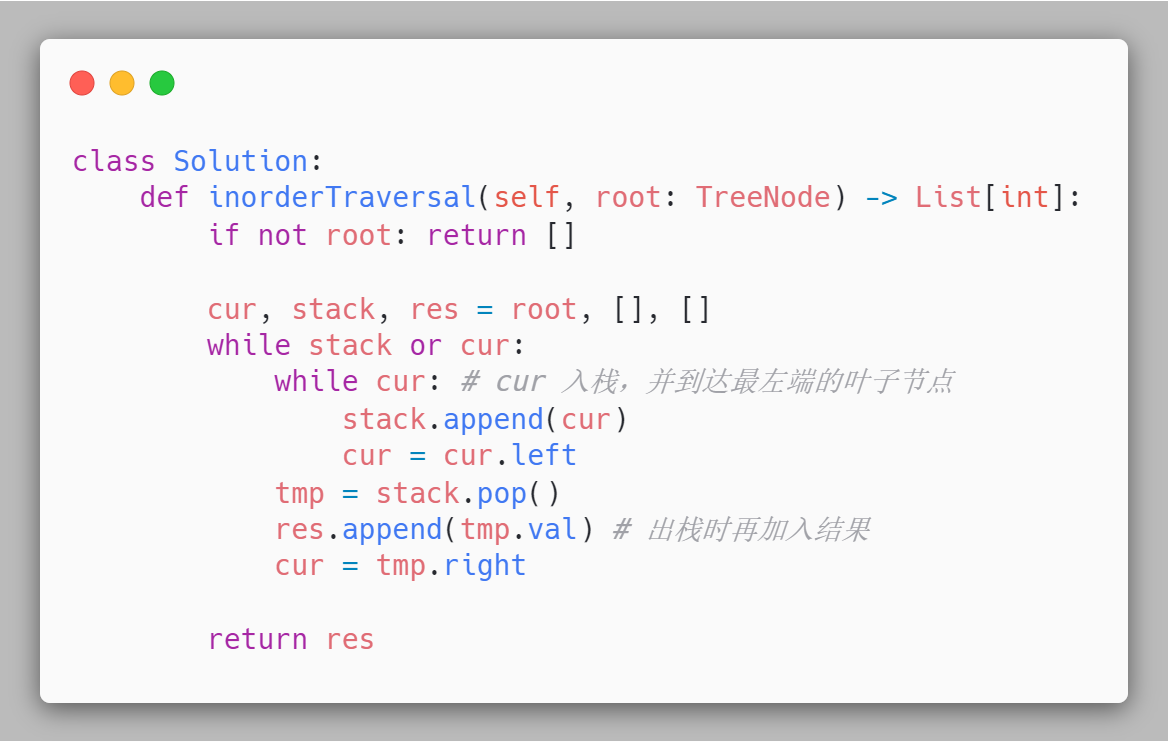
3. 二叉树的后序遍历

LeetCode 题目：145. 二叉树的后序遍历

模板解法

继续按照上面的思想，这次我们反着思考，节点 cur 先到达最右端的叶子节点并将路径上的节点入栈；

然后每次从栈中弹出一个元素后，cur 到达它的左孩子，并将左孩子看作 cur 继续执行上面的步骤。

最后将结果反向输出即可。参考代码如下：

然而，后序遍历采用模板解法并没有按照真实的栈操作，而是利用了结果的特点反向输出，不免显得技术含量不足。

因此掌握标准的栈操作解法是必要的。

常规解法

类比前序遍历的常规解法，我们只需要将输出的“根 -> 左 -> 右”的顺序改为“左 -> 右 -> 根”就可以了。

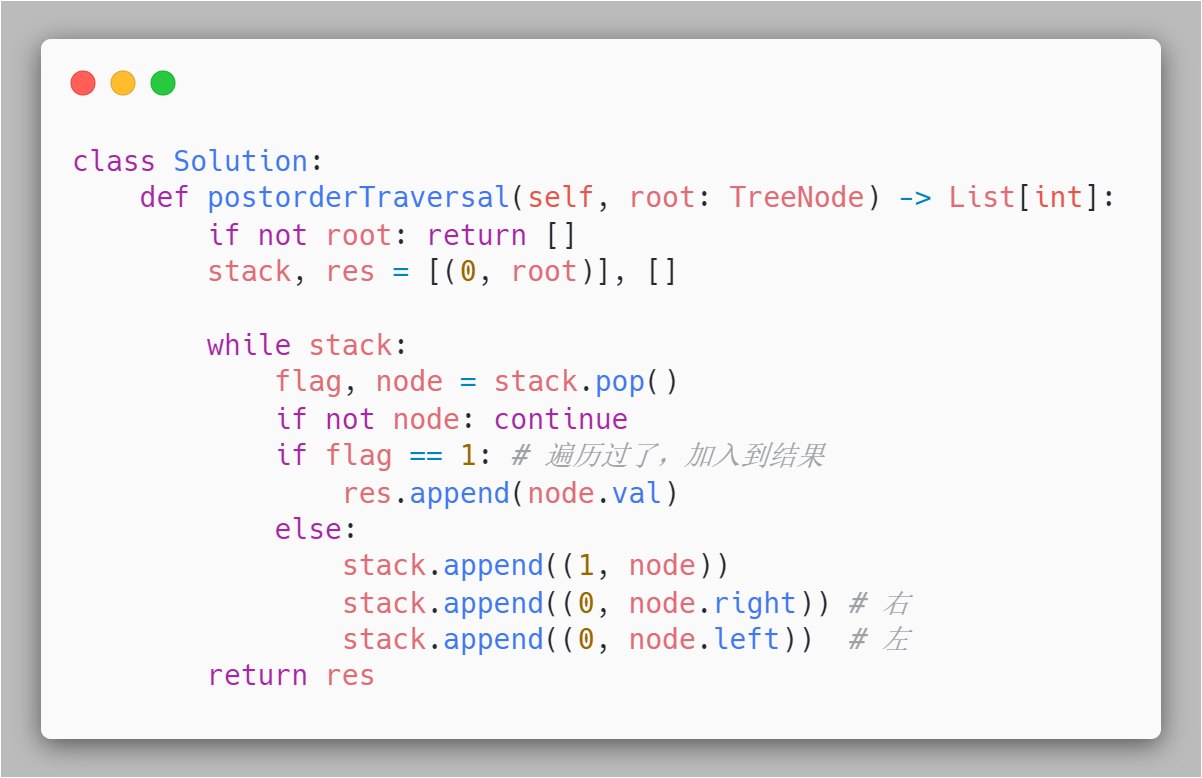
如何实现呢？这里右一个小技巧，我们入栈时额外加入一个标识，比如这里使用 flag = 0；

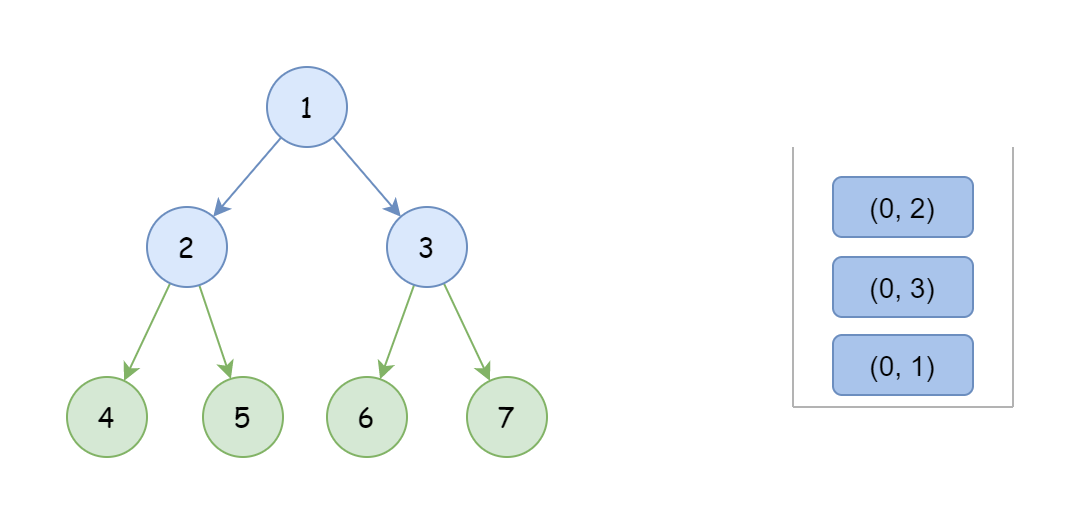
然后每次从栈中弹出元素时，如果 flag 为 0,则需要将 flag 变为 1 并连同该节点再次入栈，只有当 flag 为 1时才可将该节点加入到结果中。

参考代码如下：

4. 二叉树的层次遍历

LeetCode 题目：102. 二叉树的层序遍历

二叉树的层次遍历的迭代方法与前面不用，因为前面的都采用了深度优先搜索的方式，而层次遍历使用了广度优先搜索，广度优先搜索主要使用队列实现，也就不能使用前面的模板解法了。

广度优先搜索的步骤为：

• 初始化队列 q，并将根节点 root 加入到队列中；
• 当队列不为空时：
  • 队列中弹出节点 node，加入到结果中；
  • 如果左子树非空，左子树加入队列；
  • 如果右子树非空，右子树加入队列；

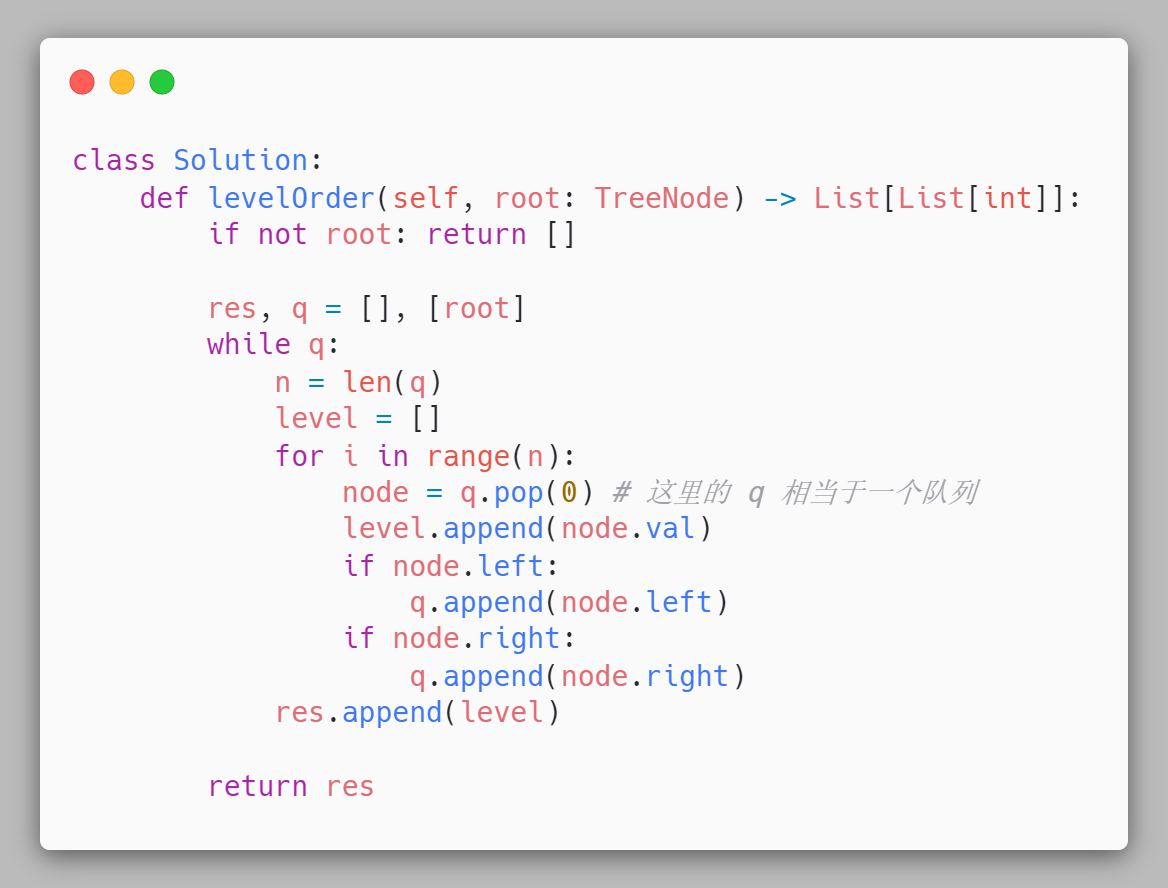
由于题目要求每一层保存在一个子数组中，所以我们额外加入了 level 保存每层的遍历结果，并使用 for 循环来实现。

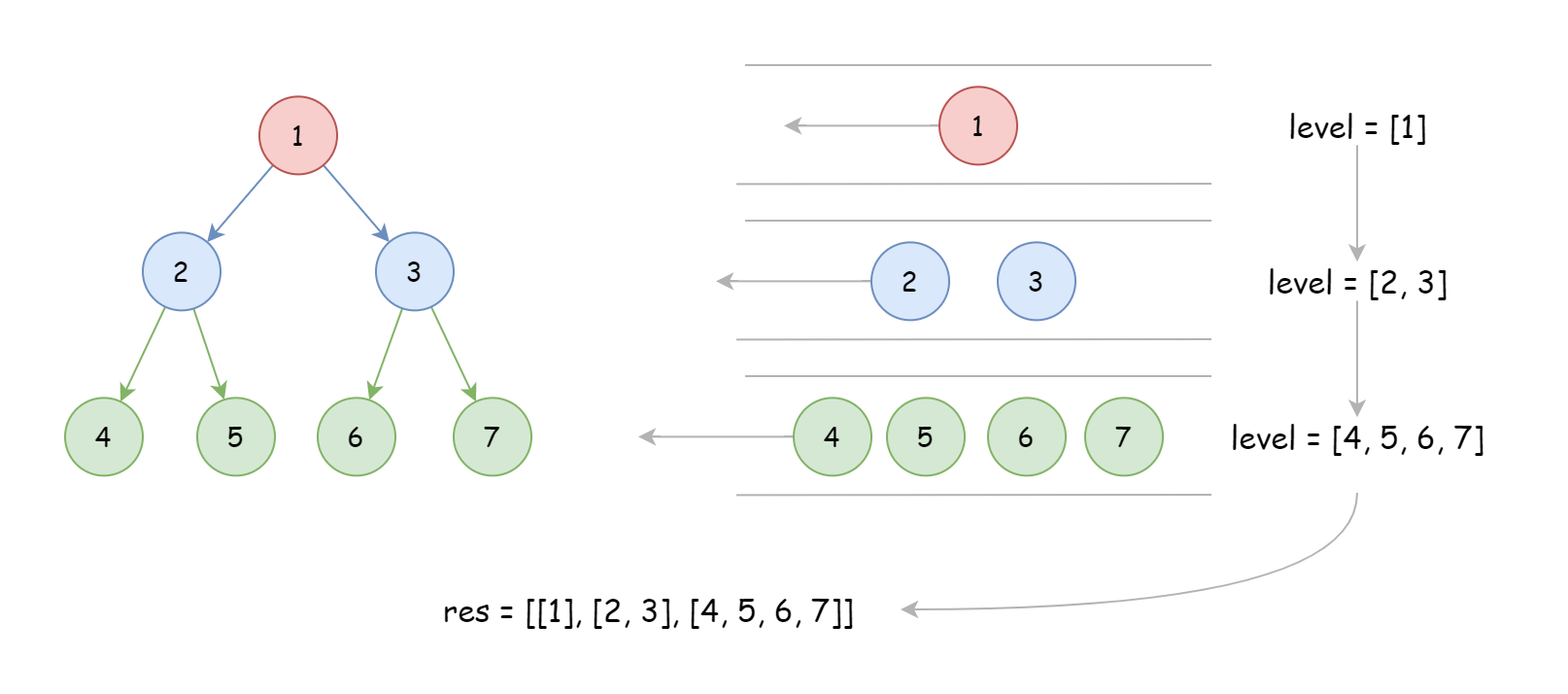
参考代码如下：

总结

总结一下，在二叉树的前序、中序、后序遍历中，递归实现的伪代码为：

迭代实现的伪代码为：

掌握了以上基本的遍历方式，对待更多的进阶题目就游刃有余了。