洛谷 p2764 、 p2765(最小路径覆盖模型 求最大流)
题意:给出一个n个点,m条边的有向无环图,求出最小路径覆盖条数,并输出。
思路:二分图有个很重要的定理就是:最小路径覆盖=点数-最大匹配。
所以要从最小路径覆盖模型转换成求二分图最大匹配。
这就是一个简单的二分图匹配的问题了。
代码:

#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int maxn=500; const int maxm=15000; struct node{ int u,v,w,nxt; }e[maxm]; int mat[maxn],h[maxn],used[maxn]; int vis[maxn],color[maxn],path[maxn]; int cnt,n,m; void add(int u,int v) { e[cnt].u=u,e[cnt].v=v; e[cnt].nxt=h[u];h[u]=cnt++; } bool find(int x) { for(int i=h[x];i!=-1;i=e[i].nxt) { int v=e[i].v; if(!used[v]) { used[v]=1; if(!mat[v]||find(mat[v])) { mat[v]=x; path[x]=v; return true; } } } return false; } int match()//匈牙利算法 { int ans=0; for(int i=1;i<=n;i++) { if(!path[i]) { memset(used,0,sizeof(used)); if(find(i)) ans++; } } return ans; } void dfs(int x)//搜索输出路径 { color[x]=1; printf("%d ",x); if(!path[x]) return ; dfs(path[x]); } void init()//初始化 { cnt=0; memset(h,-1,sizeof(h)); memset(vis,0,sizeof(vis)); memset(color,0,sizeof(color)); memset(path,0,sizeof(path)); memset(mat,0,sizeof(mat)); } int main() { int u,v; init(); scanf("%d%d",&n,&m); for(int i=0;i<m;i++) { scanf("%d%d",&u,&v); add(u,v); } int num=match(); for(int i=1;i<=n;i++) { if(!color[i]) dfs(i),printf("\n"); } printf("%d\n",n-num); return 0; }
当然,主要了解一下用网络流来解决最小路覆盖问题。
主要是建图问题,首先是要构建二分图,就是拆点了。
然后正常的用网络流解决二分图匹配问题。
拆点的意思就是将一个点 x拆成 x,x', x表示出度,x'表示入度, 即二分图中 x 是连向其他点, x'是被其他点连接 (除源点,汇点以外)。
这样图就变成了二分图。 左边都是每个点的拆点x, 右边都是每个点的拆点 x'。
网络流建图:
例如:现在有一条边 (x,y)
这建图: 源点 --->x, x---->汇点。 源点--->y, y--->汇点。 x---->y'。流量都为1。
当然都要建反向边 流量为0(这就是网络流里的知识了)。
这样每增加 1 流量说明二分图中 1 个匹配。所以答案就是 点数-最大流。
这里还原路径,用了并查集,因为二分图中路径有流量通过,说明两点匹配了。
代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int maxn=500; const int maxm=15000; struct node{ int u,v,f,c,nxt;//f表示路径流量,c表示路径容量 }e[maxm]; int h[maxn],fa[maxn],depth[maxn]; int cnt,n,m,st,ed; void add(int u,int v,int w)//建边 { e[cnt].u=u,e[cnt].v=v; e[cnt].f=0,e[cnt].c=w; e[cnt].nxt=h[u];h[u]=cnt++; e[cnt].u=v,e[cnt].v=u;//反向边 e[cnt].f=0,e[cnt].c=0; e[cnt].nxt=h[v];h[v]=cnt++; } bool bfs()//dinic--分层图 { queue<int> q; memset(depth,0,sizeof(depth)); q.push(st); depth[st]=1; while(!q.empty()) { int u=q.front();q.pop(); if(u==ed) return true; for(int i=h[u];i!=-1;i=e[i].nxt) { int v=e[i].v; if(!depth[v]&&e[i].c-e[i].f) { depth[v]=depth[u]+1; q.push(v); } } } return false; } int dfs(int u,int flow)//dinic--求点u流入汇点最大流量 { int res=flow; if(u==ed) return res; for(int i=h[u];i!=-1;i=e[i].nxt) { int v=e[i].v; if(depth[v]==depth[u]+1&&e[i].c-e[i].f) { int tmp=e[i].c-e[i].f; int di=dfs(v,min(tmp,flow)); e[i].f+=di; e[i^1].f-=di; flow-=di; } } return res-flow; } int find(int x){ return fa[x]==x?x:fa[x]=find(fa[x]);} void out(int x)//输出路径 { printf("%d ",x); for(int i=h[x];i!=-1;i=e[i].nxt) { if(e[i].f>0&&e[i].v>n) out(e[i].v-n); } } void solve() { int num=0; while(bfs()) { num+=dfs(st,inf);//最大流 } for(int i=1;i<=n;i++) fa[i]=i; for(int i=0;i<cnt;i++)//并查集 { if(e[i].u>=1&&e[i].u<=n&&e[i].v>n&&e[i].v<ed&&e[i].f>0) { if(find(e[i].u)!=find(e[i].v-n)) fa[find(e[i].v-n)]=find(e[i].u); } } for(int i=1;i<=n;i++) { if(find(i)==i) out(i),printf("\n"); } printf("%d\n",n-num);//点数-最大流 } int main() { int u,v; cnt=0; memset(h,-1,sizeof(h)); scanf("%d%d",&n,&m); st=0,ed=2*n+1; for(int i=0;i<m;i++) { scanf("%d%d",&u,&v); add(u,v+n,1);//这里 v+n代表拆点 v' } for(int i=1;i<=n;i++) { add(st,i,1);//源点st-->每一个点 add(i+n,ed,1);//每一个点-->汇点ed } solve(); return 0; }
题意:
假设有n根柱子,现要按下述规则在这n根柱子中依次放入编号为1,2,3,...的球。
(1)每次只能在某根柱子的最上面放球。
(2)在同一根柱子中,任何2个相邻球的编号之和为完全平方数。
试设计一个算法,计算出在n根柱子上最多能放多少个球。例如,在4 根柱子上最多可放11 个球。
思路:一开始很难想到这是一道图论题。 当然是可以找规律找出来答案来,但是实力有限,只看得懂网络流的方法。
我们知道如果将每一个珠子当一个点,而编号相加等于平方数 的连边,就构成了一个图。
如下所示(盗一下图 *-*):
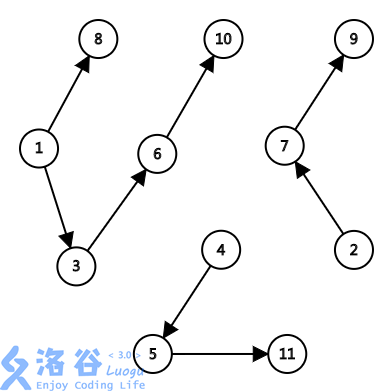
问题是“n根柱子最多放多少个珠子”,可以看做“给定珠子数量,最少要几根柱子放的下”。
给点了珠子,就是点数,而我们知道其中边的情况,求几根柱子就是几条路,这样是不是就转化成一个最小路径覆盖问题了呢?
但是这里要明白是一个珠子一个珠子放入,我们要模拟一个一个珠子放入。
再建图,求点数-最大流是否大于柱子数。
建图:
当然,和上面那道题一样,拆点,源点连x, x'连汇点。
但是两点之间有点麻烦,假设现在是编号num的珠子进入,那么,它和之前的珠子合成的平方和 >num , <num*num。
这样只要for循环找其中的平方和,用平方和- num 连向 num 即可。
代码中用偶数表示拆点 x, 奇数表示 拆点 x'。
代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> #include<cmath> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int maxn=100050; const int maxm=105000; struct node{ int u,v,f,c,nxt; }e[maxm]; int h[maxn],fa[maxn],depth[maxn]; int cnt,n,m,st,ed; void add(int u,int v,int w) { e[cnt].u=u,e[cnt].v=v; e[cnt].f=0,e[cnt].c=w; e[cnt].nxt=h[u];h[u]=cnt++; e[cnt].u=v,e[cnt].v=u; e[cnt].f=0,e[cnt].c=0; e[cnt].nxt=h[v];h[v]=cnt++; } bool bfs() { queue<int> q; memset(depth,0,sizeof(depth)); q.push(st); depth[st]=1; while(!q.empty()) { int u=q.front();q.pop(); if(u==ed) return true; for(int i=h[u];i!=-1;i=e[i].nxt) { int v=e[i].v; if(!depth[v]&&e[i].c-e[i].f) { depth[v]=depth[u]+1; q.push(v); } } } return false; } int dfs(int u,int flow) { int res=flow; if(u==ed) return res; for(int i=h[u];i!=-1;i=e[i].nxt) { int v=e[i].v; if(depth[v]==depth[u]+1&&e[i].c-e[i].f) { int tmp=e[i].c-e[i].f; int di=dfs(v,min(tmp,flow)); e[i].f+=di; e[i^1].f-=di; flow-=di; } } return res-flow; } int find(int x){ return fa[x]==x?x:fa[x]=find(fa[x]);} int dinic() { int ans=0; while(bfs()) { ans+=dfs(st,inf); } return ans; } void out(int x) { printf("%d ",x); for(int i=h[x<<1];i!=-1;i=e[i].nxt) { if(e[i].f>0&&e[i].v%2) out(e[i].v/2); } } int main() { scanf("%d",&n); cnt=0; memset(h,-1,sizeof(h)); st=0,ed=2*n+1; int t=0,num=0; while(1) { num++;//模拟一个个珠子进入 add(st,num<<1,1);add((num<<1)|1,ed,1); //num<<1偶数表示x, num<<1|1奇数表示x' for(int i=sqrt(num)+1;i*i<2*num;i++)//用前面可以连接num珠子连接num(x') add((i*i-num)<<1,(num<<1)|1,1); t+=dinic();//最大流,因为前面已经求了,所以是加上num带来的流量 if(num-t>n) break;//点数-最大流 } printf("%d\n",--num); for(int i=1;i<=num;i++) fa[i]=i; for(int i=0;i<cnt;i++)//并查集 { if((e[i].u%2==0)&&(e[i].v%2==1)&&e[i].f>0) { if(find(e[i].u/2)!=find(e[i].v/2)) fa[find(e[i].v/2)]=find(e[i].u/2); } } for(int i=1;i<=num;i++) { if(find(i)==i) out(i),printf("\n"); } return 0; }





