poj 2942 Knights of the Round Table(点双连通分量)

题目链接：http://poj.org/problem?id=2942

 

转载自：https://blog.csdn.net/lyy289065406/article/details/6756821

 

大致题意：

亚瑟王要在圆桌上召开骑士会议，为了不引发骑士之间的冲突，并且能够让会议的议题有令人满意的结果，每次开会前都必须对出席会议的骑士有如下要求：

1、  相互憎恨的两个骑士不能坐在直接相邻的2个位置；

2、  出席会议的骑士数必须是奇数，这是为了让投票表决议题时都能有结果。

 

如果出现有某些骑士无法出席所有会议（例如这个骑士憎恨所有的其他骑士），则亚瑟王为了世界和平会强制把他剔除出骑士团。

       现在给定准备去开会的骑士数n，再给出m对憎恨对（表示某2个骑士之间使互相憎恨的），问亚瑟王至少要剔除多少个骑士才能顺利召开会议？

 

注意：1、所给出的憎恨关系一定是双向的，不存在单向憎恨关系。

2、由于是圆桌会议，则每个出席的骑士身边必定刚好有2个骑士。即每个骑士的座位两边都必定各有一个骑士。

3、一个骑士无法开会，就是说至少有3个骑士才可能开会。

 

解题思路：

综合性非常强的图论题，在说解题报告之前，我建议大家先对以下内容有所认识，否则本题是很难做下去的：

 

1、补图 的定义

2、双连通分量 的定义

3、二分图 的定义

4、奇圈 的定义

5、判定一个图是否为二分图的方法：交叉染色法

6、Tarjan算法

为了方便大家做题，我这里大概第说一下上述的6个知识点，注意下述是我通俗的理解，不是标准定义：

1、 补图

图G的补图~G就是把图G原有的边全部删去，原本不存在的边全部连上。

 

2、双连通分量

       简单来说，无向图G如果是双连通的，那么至少要删除图G的2个结点才能使得图G不连通。换而言之，就是图G任意2个结点之间都存在两条以上的路径连接（注意：路径不是指直接相连的边），那么双连通分量就是指无向图G的子图G’是双连通了。

 

3、二分图

       二分图又叫二部图，这个百度百科有定义，了解一下二分图是什么样子的可以了，无需深入去了解。不懂得同学等到做二分图的题目时再认真学吧。

 

4、 奇圈

用一条线把奇数个点串连起来，所得到的闭合的圈就是奇圈了。其实奇圈就是有奇数个顶点的环。

 

5、交叉染色法判定二分图

       初始化所有结点为无色（颜色0）状态，用DFS遍历一个图G的同时，顺便对结点染色（只染1、2色），注意遍历过的结点还可以再遍历重新上色。让遍历到某个时候在对结点t染色时，发现边s->t的另一个结点s已染色，且s的颜色与当前正在对t染的颜色相同，那么图G必定不是二分图。

       这是因为想象一下二分图就像是河的两岸有两排结点，每染色一次则过河一次，那么相同颜色的结点必定在同一侧。一旦出现异侧有相同颜色的结点，就可以说明图G不是二分图了。

 

6、Tarjan算法

       我希望大家主要去学习一下这个算法的基本原理，尤其是DFN数组和Low数组，还有什么是深搜树，什么是树枝边，什么是后向边。

学习一下Tarjan算法求割点的过程（注意我上文是建议大家不要用Tarjan算法去求解割点的题，但不是让大家不要看它求割点的过程），因为这个过程是求双连通分量的关键。

       而如果想很好地了解Tarjan算法求割点的过程，还是建议先去看刘汝佳的《算法艺术与信息学竞赛》P285页，然后去做一下POJ1523（纯粹求割点的题）找点感觉。

只要弄懂了刘汝佳的方法，再看Tarjan算法就非常容易理解了。

 

有了上述知识支撑，可以开始解题了：

1、  利用m对憎恨对构造图G，则图G中有边相连的两个点表示这2个骑士互相憎恨。

2、  构造图G的补图~G，则图~G中有边相连的两个点表示这2个骑士可以坐在相邻位置。

3、  在图~G中，可能存在某些点的度数<=1，就是说这些骑士旁边最多只能坐另一个骑士，根据圆桌的座位要求每个骑士k的座位两边都必定各有一个骑士（k度数==2），那么我们认为这些度数<=1的点是孤立的或者是单连通的，也就是说他们不在圆桌的“环”内。

 

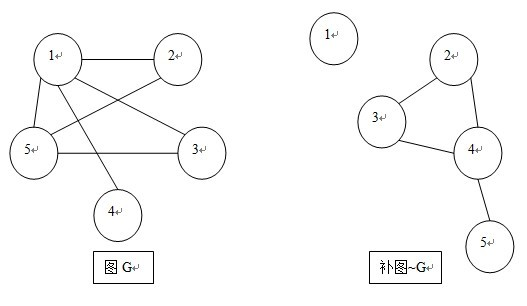
例如上图，我们利用图G构造补图~G后，显然骑士1的度=0，他是孤立的、不连通的；骑士5的度=1，他是单连通的；骑士{2,3,4}则构成一个双连通分量，他们正在圆桌“环”内开会。显然度数<=1的骑士1和骑士5都在环外，不满足出席会议的条件，亚瑟王为了维护世界和平自然会把这2人驱逐出骑士团。

 

4、  现在问题是，我们怎么才能知道哪些骑士在环外？

我们可以把问题转化为，我们怎么才能知道哪些骑士在环内？显然在环内的所有结点都是双连通的，我们可以通过Tarjan算法求双连通分量。注意，补图~G可能有几个双连通子图，即它可能有不止一组双连通分量，而Tarjan算法是一组一组双连通分量求出来的，因此每求出一组双连通分量我们就要马上处理一组。

下面都是针对某一组双连通分量的处理。

 

5、  骑士在双连通分量内（在环内），并不能就此就说明它可以出席会议了，因为假如这个骑士所在的双连通分量，不是一个奇数顶点的环（奇圈），而是一个偶数顶点的环，那么这个双连通分量内的全部骑士都要被亚瑟王开除。

 

6、  那么怎样判断一个双连通分量是奇圈呢？

首先我们要接受两条定理，想知道证明过程的可以上网找，这里不证明：

（1）       如果一个双连通分量内的某些顶点在一个奇圈中（即双连通分量含有奇圈），那么这个双连通分量的其他顶点也在某个奇圈中；

（2）       如果一个双连通分量含有奇圈，则他必定不是一个二分图。反过来也成立，这是一个充要条件。

由于双连通分量也是一个图，那么要判断双连通分量是否为奇圈，只需判断这个双连通分量是否为一个二分图，而要判断一个图是否为二分图，就用交叉染色法！

 

7、  显然所有在奇圈中的骑士，都是允许出席会议的，而由于可能有部分骑士允许出席一个以上的会议（即他们是2个以上的奇圈的公共点），那么为了避免重复统计人数，当我们判断出哪些骑士允许出席会议时，就把他们做一个标记（相同的骑士只做一个标记）。最后当Tarjan算法结束后，我们统计一下被标记的人数有多少，再用总人数减去这部分人，剩下的就是被亚瑟王剔除的人数了。

 

上面的内容已经写得很详细了，我是用这个题目和这篇博客入门点双连通分量的。

说说我的一点理解：当dfn[u]<=low[v]，说明u是割点，这时只要取出一个个点，直到v即边(u,v），但割点u可以认为在这个点双连通分支里，割点是可以属于多个双连通分支,。

这里是和缩点不同的是：不是值到取至u。很明显我们是取出一个双连通分支，而不是全部的点。

 代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1010;
const int maxm=2000010;
struct node{
    int u,v,nxt;
}e[maxm];
int h[maxn],color[maxn];
bool inst[maxn],ok[maxn],flag[maxn];
int st[maxn],dfn[maxn],low[maxn],tp[maxn];
int cnt,top,tot,num,scc,n,m; 
bool g[maxn][maxn];

void add(int u,int v)
{
    e[cnt].u=u,e[cnt].v=v;
    e[cnt].nxt=h[u],h[u]=cnt++;
}

void init()//初始化 
{
    memset(h,-1,sizeof(h));
    memset(inst,0,sizeof(inst));
    memset(dfn,0,sizeof(dfn));
    memset(flag,0,sizeof(flag));
    memset(g,0,sizeof(g));
    cnt=tot=top=num=scc=0;
}

bool dfs(int x,int cl)//染色,判断是否是二分图 
{
    color[x]=cl;
    for(int i=h[x];i!=-1;i=e[i].nxt)
    {
        int v=e[i].v;
        if(!ok[v]) continue;
        if(color[v]==cl) return false;
        if(!color[v]&&!dfs(v,-cl)) return false;
    }
    return true;
}

void tarjan(int u,int pre) 
{
    low[u]=dfn[u]=++tot;
    st[top++]=u;
    inst[u]=1;
    int pre_cnt=0;
    for(int i=h[u];i!=-1;i=e[i].nxt)
    {
        int v=e[i].v;
        if(v==pre&&pre_cnt==0)
        {
            pre_cnt++;
            continue;
        }
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<=low[v])//找到u是割点 
            {
                memset(ok,0,sizeof(ok));
                int t;
                scc=0; 
                do{
                    t=st[--top];
                    inst[t]=0;
                    ok[t]=1;//标记，用于染色 
                    tp[scc++]=t;//存点双连通分量 
                }while(t!=v);
                ok[u]=1;
                memset(color,0,sizeof(color));
                if(!dfs(u,1))//不是二分图，则是奇圈，则标记可以开会的骑士 
                {
                    flag[u]=1;
                    while(scc--)
                        flag[tp[scc]]=1;
                }
            }
        }
        else if(inst[v])
            low[u]=min(low[u],dfn[v]);
    }
}

void solve()
{
    int ans=n;
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i,-1);
    for(int i=1;i<=n;i++)
        if(flag[i])
            ans--;
    printf("%d\n",ans);
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(!n&&!m) break;
        init();
        int u,v;
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            g[u][v]=g[v][u]=1;
        }
        for(int i=1;i<=n;i++)//建补图 
            for(int j=1;j<=n;j++)
                if(i!=j&&!g[i][j])
                    add(i,j);
        solve();
    }
    return 0;
}