树状数组总结
动态求前缀和的数据结构。
可以解决的问题:数组中单点修改,求区间前缀和;区间修改,求区间前缀和;求逆序对;求数组中动态删去一个数时,第k大数等等。
求逆序对(楼兰图腾)
题意

用树状数组求出,每个数之前有多个数大与这个数的,小于这个数的(正向循环)
用树状数组求出,每个数之后有多少个与这个数的,小于这个数的,(反向循环)
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <stdio.h>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <string.h>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <list>
#include <iomanip>
#include <numeric>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(s) memset(s, 0, sizeof(s))
const int INF = 0x3f3f3f3f;
#define LOCAL
const int N=1e6+100;
int n,a[N];
ll _great[N],_low[N],tr[N];
int lowbit(int x)
{
return x&-x;
}
void add(int c,int v)
{
for(int i=c;i<=n;i+=lowbit(i))
tr[i]+=v;
}
ll sum(int x)
{
ll res=0;
for(int i=x;i;i-=lowbit(i))
res+=tr[i];
return res;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
int y=a[i];
_great[y]=sum(n)-sum(y);
_low[y]=sum(y-1);
add(y,1);
}
memset(tr,0,sizeof tr);
ll res1=0,res2=0;
for(int i=n;i;i--)
{
int y=a[i];
res1 += _great[y] * (sum(n)-sum(y));
res2 += _low[y] * sum(y-1);
add(y,1);
}
cout<<res1<<' '<<res2<<endl;
return 0;
}
单点修改、区间查询(一个简单的整数问题)
题意
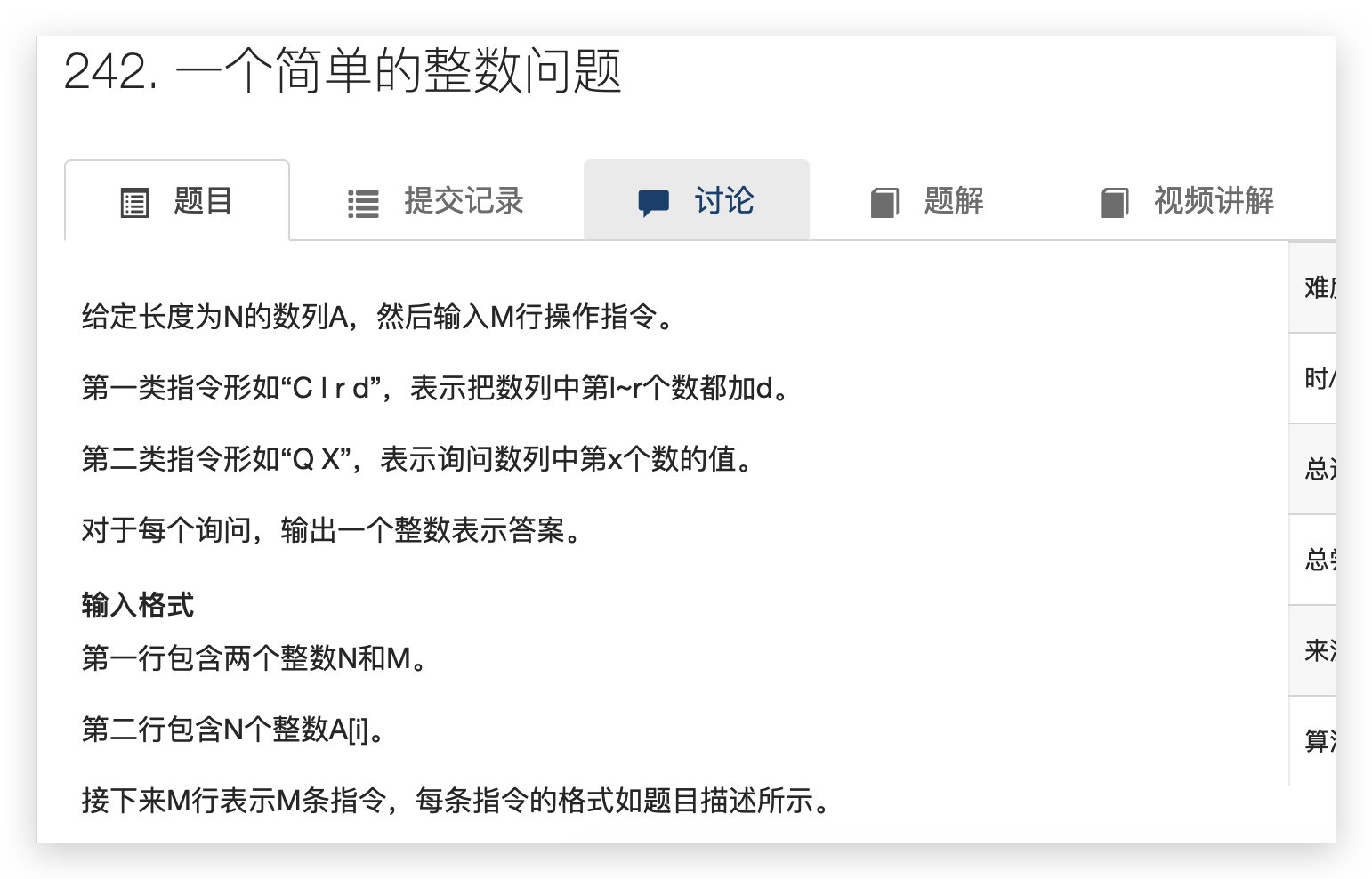
思路
修改一个数,相当与+这个数与原数的差,剩下都是树状数组的函数
代码
#include<iostream>
#include<string>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const double eps = 1e-5;
const int N=1e6;
int a[N],n,m;
ll tr[N];
int lowbit(int x)
{
return x&-x;
}
ll sum(int x)
{
ll res=0;
for(int i=x;i>=1;i-=lowbit(i))
res+=tr[i];
return res;
}
void add(int id,int x)
{
for(int i=id;i<=n;i+=lowbit(i))
tr[i]+=x;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) add(i,a[i]-a[i-1]);
while(m--)
{
char op[3];
cin>>op;
if(op[0]=='C')
{
int l,r,x;
cin>>l>>r>>x;
add(l,x),add(r+1,-x);
}
else{
int x;
cin>>x;
cout<<sum(x)<<endl;
}
}
return 0;
}
区间修改、单点查询(一个简单的整数问题2)
题意

思路
区间修改:转化为差分数组
区间查询:转化为前缀和查询
前缀和查询:
代码
#include<iostream>
#include<string>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const double eps = 1e-5;
const int N=1e6;
ll a[N],n,m;
ll tr1[N],tr2[N];
ll lowbit(ll x)
{
return x&-x;
}
ll sum(ll tr[],ll x)
{
ll res=0;
for(int i=x;i>=1;i-=lowbit(i))
res+=tr[i];
return res;
}
void add(ll tr[],int id,ll x)
{
for(int i=id;i<=n;i+=lowbit(i))
tr[i]+=x;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) add(tr1,i,a[i]-a[i-1]),add(tr2,i,i*(a[i]-a[i-1]));
while(m--)
{
char op[3];
cin>>op;
if(op[0]=='C')
{
int l,r,x;
cin>>l>>r>>x;
add(tr1,l,x),add(tr1,r+1,-x);
add(tr2,l,x*l),add(tr2,r+1,(r+1)*(-x));
}
else{
int l,r;
cin>>l>>r;
cout<<sum(tr1,r)*(r+1) - sum(tr2,r) - (sum(tr1,l-1)*(l) - sum(tr2,l-1))<<endl;
}
}
return 0;
}
动态求第k大数(谜一样的牛)
题意

思路
数组中每个数代表是前面的第K+1个大的数,那么最后一个数,就可以确定出来,以此类推,从后往前就可以推出所有的数。期间,确定好的数之后就不会再出现。
求第k大的数,可以用二分+前缀和的思路求。找到这个数,就在树状数组中下标是这个数就删去。
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <stdio.h>
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <string>
#include <string.h>
#include <cstring>
#include <algorithm>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <ctime>
#include <vector>
#include <fstream>
#include <list>
#include <iomanip>
#include <numeric>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(s) memset(s, 0, sizeof(s))
const int INF = 0x3f3f3f3f;
#define LOCAL
const int N=1e6+100;
int n,a[N];
ll tr[N];
int lowbit(int x)
{
return x&-x;
}
void add(int c,int v)
{
for(int i=c;i<=n;i+=lowbit(i))
tr[i]+=v;
}
ll sum(int x)
{
ll res=0;
for(int i=x;i;i-=lowbit(i))
res+=tr[i];
return res;
}
int st[N];
int main()
{
cin>>n;
for(int i=2;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) add(i,1);
for(int i=n;i;i--)
{
int k = a[i] + 1;
int l = 1, r = n;
while (l < r)
{
int mid = l + r >> 1;
if (sum(mid) >= k) r = mid;
else l = mid + 1;
}
add(r,-1);
st[i]=r;
}
for(int i=1;i<=n;i++) cout<<st[i]<<endl;
return 0;
}



 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号