数据结构包括三个内容：
1.数据元素之间的逻辑关系，也称为逻辑结构。
2.数据元意及其关系在计算机内得中的表示《又称为映像），称为数
据的物理结构或数据的存储结构。
3.数据的运算和实现，即对数据无素可以施加的操作以及这些操作在
相应的存储结构上的实现。

逻辑结构

描述数据元素之间的逻辑关系
与数据的存储无关，独立于计算机
是从具体问题抽象出来的数学模型

逻辑结构的表示：

1、图表表示

采用表格或者图形直接描述数据的逻辑关系

学号	姓名	性别	班号
1	张三	男	2020
8	李四	女	2021
34	王琦	女	2022
20	刘丽	男	2023

2、二元组表示

二元组是一个通用的逻辑数据结构表示方法

例：B=(D,R)

B——数据结构
D——数据元素的集合
R——D上二元关系的集合

D={di|1≤i≤n,n≥0 } di表示集合D中第i个数据元素，n表示D中数据元素的个数，若n=0，D是一个空集，具有任意结构

R={rj|1≤j≤m,m≥0 } rj表示集合R中的第j个关系，m为R中关系的个数，若m=0，R是一个空集，集合D中的数据元素间不存在任何逻辑关系。

R中的一个关系r，是序偶的集合，对于r中的任一序偶<x,y>(x，y ∈ D），表示元素x和y之间是相邻的，即x在y之前，y在x之后，x称为该序偶的第一元素，y称为该序偶的第二元素，而且x为y的直接前驱元素(predecessor),y为x的直接后继元素(successor)。为了简便，将直接前驱元素和直接后继元素分别简称为前驱元素和后继元素。
若某个元素没有前驱元素，则称该元素为开始元素（first element）；若某个元素没有后继元素，则称该元素为终端元素(terminal element）。
对于对称序偶，即<x,y> ∈ r,则<y,x> ∈ r(x，y ∈ D)，可用圆括号代替尖括号，即（x，y) ∈ r。在用图形表示逻辑关系时，对称序偶用不带箭头的连线表示。

根据上面所描述知道了二元组的表示方法，那么再对于学生表的逻辑结构二元组表示，如下所示：学生表 = （D，R）

D = {100，101，102，103}
R = {r}
r = {<100，101>，<101，102>，<102，103>}

逻辑结构的类型

线性结构：有且仅有一个开始和一个终端结点，并且所有结点都最多只有一个直接前驱和一个直接后继。是一对一的关系。例如：线性表，栈，队列，串。

非线性结构：一个结点可能有多个直接前驱和直接后继。例如：数，图

树形结构：数据元素存在一对多的关系。特点是除了开始元素以外，每个元素有且仅有一个前驱元素，除了终端元素以外，每个元素有一个或者多个后继元素。
图形结构：数据元素存在多对多的关系。其特点是每个元素的前驱元素和后继元素的个数可以是任意的。

集合：数据元素除了同属于一个集合的关系以外别无其他关系。

存储结构

数据元素与数据元素在计算机存储器中的结构(存储方式)
是数据结构在计算机中的表示

存储结构的种类

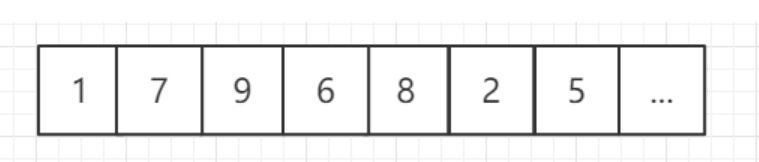
顺序存储结构：用一组连续的存储单元依次存储数据元素，数据元素之间的逻辑关系由元素的存储位置来表示。

优点：存储效率高

缺点：不便于数据修改

C语言中用数组来实现顺序存储结构
链式存储结构：用一组任意的存储单元存储数据元素，数据元素之间的逻辑关系用指针来表示。

优点：便于数据的修改

缺点：空间利用率低

由head所指结点的next域下一个结点的信息。
索引存储结构：在存储结点信息的同时，还建立附加的索引表。

优：查找效率高

缺：增加空间开销
哈希(散列)存储结构：根据结点的关键字通过哈希函数直接计算出该节点的存储位置。

逻辑结构和存储结构的关系

存储结构是逻辑关系的映像与元素本身的映像
逻辑结构是数据结构的抽象，存储结构是数据结构的实现

数据类型(data type)

定义：数据类型是一组性质相同的值的集合和定义在在此集合上的一组操作的总称。在使用高级程序设计语言编写程序的时候，必须对程序中出现的每个变量、常量、表达式明确说明他们所属的数据类型。

作用：约束变量或者常量的取值类型，约束变量或者常量的操作

c语言中int类型，范围为[-32768,32767]的数可以进行+、-、*、\、%等操作

例如：C语言中

提供int、 char、 float、double等基本数据类型
数组、结果、共用体、枚举等构造数据类型
还有指针、空类型
用户也可以用typedef自己定义数据类型

抽象数据类型(Abstract Data Type，ADT)

定义：指一个数学模型以及定义在数学模型上的一组操作

包括三部分：

逻辑结构：用户定义，从问题抽象出数据模型
相关操作：定义在数据模型上的一组抽象运算
算法：不考虑计算机内的uti存储结构和运算的具体实现算法

形式定义：三元组(D,S,P)

D是数据对象

S是D上的关系集

P是对D的基本操作

定义格式：

ADT 抽象类型数据名{
    数据对象：<数据对象的定义>
    数据关系：<数据关系的定义>
    基本操作：<数据操作的定义>
} ADT 抽象类型数据名

基本操作的定义格式：
	基本操作名
	初始条件
	操作结果

应用参数：以&打头，除可提供输入值外，还将返回操作结果

ADT Rational
{    数据对象：D={e1,e2|e1,e2属于ElemType类型}
     数据关系：R={<e1,e2>|e1是有理数的分子部分，e2是有理数的分母部分}
     基本操作：
            InitRat(&T,f1,f2)//构造有理数T,元素e1,e2分别被赋分v1,v2的值
            DestoryRat(&T)//T被销毁
            Get(*T,i,&e)//用e返回T的第i元的值
            Modify(&T,i,e)//修改T的第i元为e 
            Redu(&T)//有理数的化简。
            Add(*T1,*T2,&T3)//用T3返回两个有理数的和。
            subt(*T1,*T2,&T3)//用T3返回两个有理数的差。
            Mult(*T1,*T2,&T3)//用T3返回两个有理数的积。
            Division(*T1,*T2,&T3)//用T3返回两个有理数的商。
}ADT Rational

算法

定义：对特定问题的求解方法和步骤的一种描述，是指令的有限序列。

算法与程序：算法是解决问题的一种方法或者过程，一个问题可以有多种算法。程序是用某种程序设计语言对算法的具体实现。

程序= 数据结构+算法

算法特性

有穷性：算法的步骤和时间在有限的时间完成
确定性：每一条指令有确切的含义，相同的输入只能得到相同的输出
可行性：算法中的每一个动作都能够被机械的执行
有输入：一个算法有零个或者多个输入
有输出：一个算法有一个或者多个输出

算法设计的要求：

正确性：能正确解决问题，程序对于精心选择的，典型的，苛刻带有***难的数据能得出满足要求的结果。

可读性：人能理解

健壮性：输入非法数据时，算法不会出现异常情况

高效性：算法执行的时间。

算法分析

评判不同算法的优劣程度：算法的效率

算法效率：

1、时间效率：指的是算法所消耗的时间

2、空间效率：指的是算法执行过程中所耗费的存储空间

算法分析方法：

1、事前分析法

算法运行时间 = 一个简单操作所需的时间 ^ 简单操作次数的

2、事后分析法(有缺点)

算法时间复杂度分析

算法中基本语句(执行次数最多)重复执行的次数是问题规模n的某个函数f(n),算法的时间量读记作：T(n)=O(f(n)) 表示：随着n的增大，算法执行的时间的增长率和f(n)的增长率相同，称为渐近时间复杂度。

算法空间复杂度分析

算法所需存储空间的度量

S(n) = O(f(n)) n为问题的规模
空间复杂度：若输入数据所占空间只取决于问题本身，和算法无关，则只需要分析除输入和程序之外的辅助变量所占额外空间。

posted on 2023-02-25 18:05 AprilX 阅读(147) 评论(0) 编辑收藏举报

刷新页面返回顶部

公告

导航

数据结构介绍

算法