MathProblem 57 Chessboard problem #1

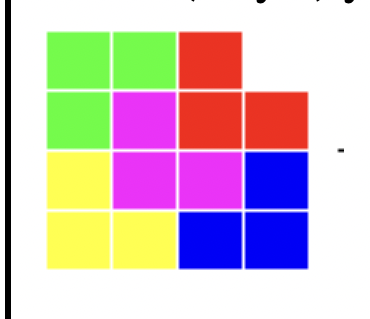
Given an \(2^n\) by \(2^n\) chessboard, with one corner removed, show that you can cover it completely without overlapping or going off the board using only triominoes of the shape below.

Rotations are allowed.

Solution

将 \(2^n\times 2^n\) 的棋盘一个顶角去掉， 用一个\(2\times 2\) 也去掉一角的图形去覆盖，问是否都可以无重叠地覆盖？

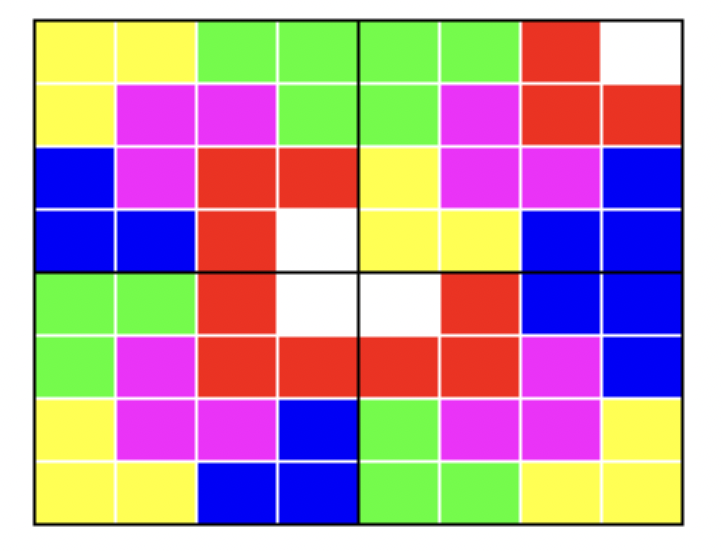
从最简单的 \(2\times 2\) 开始，显然可以；考虑 \(4\times 4\)，方法就是在最中间的那一部分用该图形覆盖，且缺角的方向保持一致，如下图所示：

那么对于 \(8\times 8\) 也是类似的：