MathProblem 29 Four dogs and a square problem
Four dogs occupy the four corners of a square with side of length a. At the same time each dog starts walking at the same speed directly toward the dog on his left. Eventually all four dogs will converge at the center of the square. What path does each dog follow and what is the distance each dog walks until he reaches the center?
Solution
考虑边长为 1 的方形,以中心为原点 \(C\)。
接着引入极坐标,设曲线上一点为 \(D\), \(CD=r\), \(CD\) 连线与横坐标夹角为 \(x\), \(CD\) 与 \(D\) 处切线夹角为 \(y\),为了方便理解,看下图:
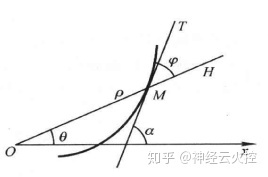
因此:
\[\begin{align}
\tan(\alpha) = \frac{dy}{dx}&=\frac{[r(x)\sin(x)]'}{[r(x)\cos(x)]'}\\
&=\frac{r'(x)\sin(x)+r(x)\cos(x)}{r'(x)\cos(x)-r(x)\sin(x)}\\
&=\frac{r'\tan(x)+r}{r'-r\tan(x)}
\end{align}
\]
另外从图中知道:\(\tan(\phi)= \tan(\alpha-\theta)=\frac{\tan(\alpha)-\tan(\theta)}{1+\tan(\alpha)\tan(\theta)}\)
所以化简一下得到:
\[\tan(y)=\frac{r}{r'(x)}=\frac{r}{dr/dx}
\]
现考虑第四象限为1号,它的目标是第一象限的2号,所以刚开始时:
\[r(x) = -dr/dx
\]
因此 \(r = c\cdot e^{-x}\),考虑初始值:可得 \(r(0)=c=\sqrt{2}/2\)



