随笔 - 54 文章 - 0 评论 - 45 阅读 - 45万

OpenCV 之角点检测

1.OpenCV 之透视 n 点问题2021-09-08 2.OpenCV 之自定义滤波2021-08-25 3.OpenCV 之特征匹配2021-08-13 4.OpenCV 之特征检测2021-08-01 5.OpenCV 之空间刚体变换2021-04-28 6.OpenCV 之平面单应性2021-04-02 7.OpenCV 之图像几何变换2021-03-25

8.OpenCV 之角点检测2021-03-11

9.OpenCV 之编译配置 4.6.02016-08-14 10.OpenCV 之 Mat 类2017-08-08 11.OpenCV 之网络摄像头2017-07-12 12.OpenCV 之神经网络 (一)2017-06-27 13.OpenCV 之图像边缘检测2016-06-05 14.OpenCV 之基本绘图2020-04-21 15.OpenCV 之支持向量机 (一)2016-07-30

角点 (corners) 的定义有两个版本：两条边缘的交点，或邻域内具有两个主方向的特征点

从人眼来看，角点是图像亮度发生剧烈变化的点或边缘曲线上曲率为极大值的点。例如，下图 E 和 F 便是典型的角点

1 检测思路

在图像中定义一个局部小窗口，然后沿各个方向移动时，会出现 a) b) c) 三种情况，分别对应平坦区、边缘和角点：

a) 窗口内的图像强度，在窗口向各个方向移动时，都没有发生变化，则窗口内都是 “平坦区”，不存在角点

b) 窗口内的图像强度，在窗口向某一个 (些) 方向移动时，发生较大变化；而在另一些方向不发生变化，那么，窗口内可能存在 “边缘”

c) 窗口内的图像强度，在窗口向各个方向移动时，都发生了较大的变化，则认为窗口内存在 “角点”

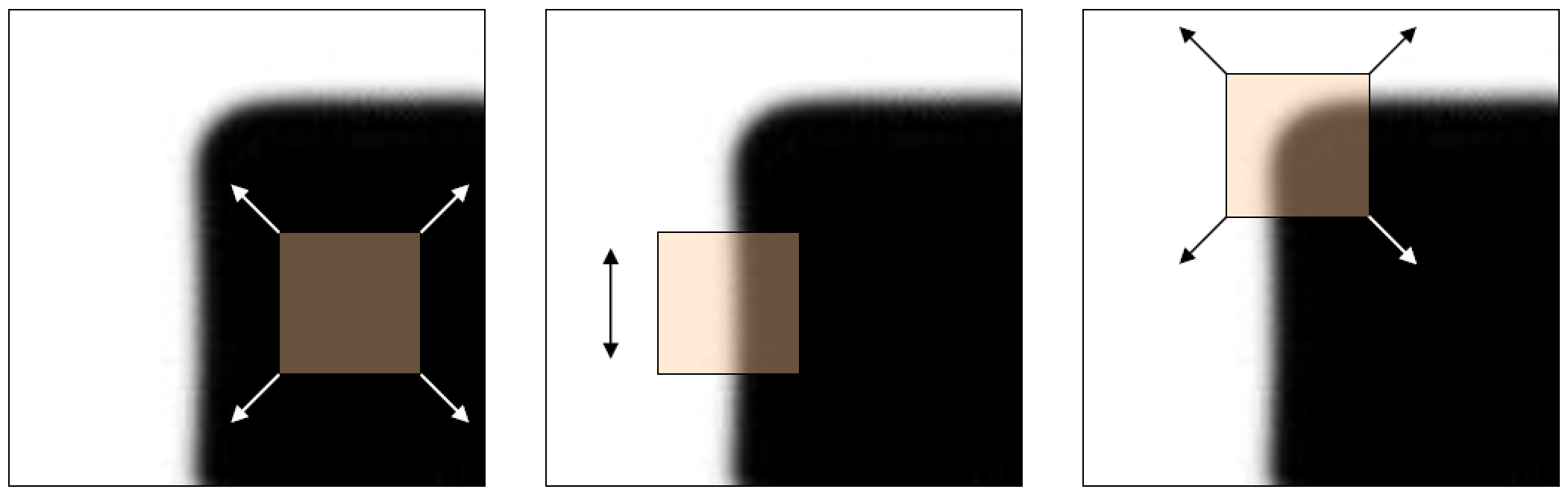
a) flat region b) edge c) corner

2 Harris 角点

2.1 泰勒展开

图像在点 $(x,y)$ 处的灰度值为 $I(x, y)$ ，当在 $x$ 方向上平移 $\Delta u$ ，且 $y$ 方向上平移 $\Delta v$ 时，图像灰度值的变化为

　 $\qquad E(\Delta u,\Delta v) = \sum\limits_{x,y} \, \underbrace{w(x,y)}_\text{window function} \; [\underbrace{I(x+\Delta u, y+\Delta v)}_\text{shifted intensity} - \underbrace{I(x, y)}_\text{intensity}]^2$

$I(x,y)$ 的偏导数分别记为 $I_x$ 和 $I_y$ ，则上式用二元一阶泰勒级数近似展开

$\qquad \sum\limits_{x,y} \; [I(x+\Delta u, y+\Delta v) - I(x, y)]^2 \approx \sum\limits_{x,y} \; [I(x, y) +\Delta uI_x + \Delta vI_y - I(x, y)]^2 = \sum\limits_{x,y} \; [\Delta u^2I_x^2 + 2\Delta u \Delta vI_x I_y + \Delta v^2I_y^2 ]$

写成矩阵形式

$\qquad E(\Delta u,\Delta v) \approx \begin{bmatrix} \Delta u & \Delta v \end{bmatrix} \left ( \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix} \right ) \begin{bmatrix} \Delta u \\ \Delta v \end{bmatrix}$

则有

$\qquad E(\Delta u,\Delta v) \approx \begin{bmatrix} \Delta u & \Delta v \end{bmatrix} M \begin{bmatrix} \Delta u \\ \Delta v \end{bmatrix}$ ，假定 $M = \displaystyle \sum_{x,y} w(x,y) \begin{bmatrix} I_x^{2} & I_{x}I_{y} \\ I_xI_{y} & I_{y}^{2} \end{bmatrix}$

2.2 判别方法

定义角点响应值 $R = det(M) - k(trace(M))^{2} = \lambda_{1} \lambda_{2} - k (\lambda_{1}+\lambda_{2})^2$ ，根据响应值的大小，判断小窗口内是否包含角点：

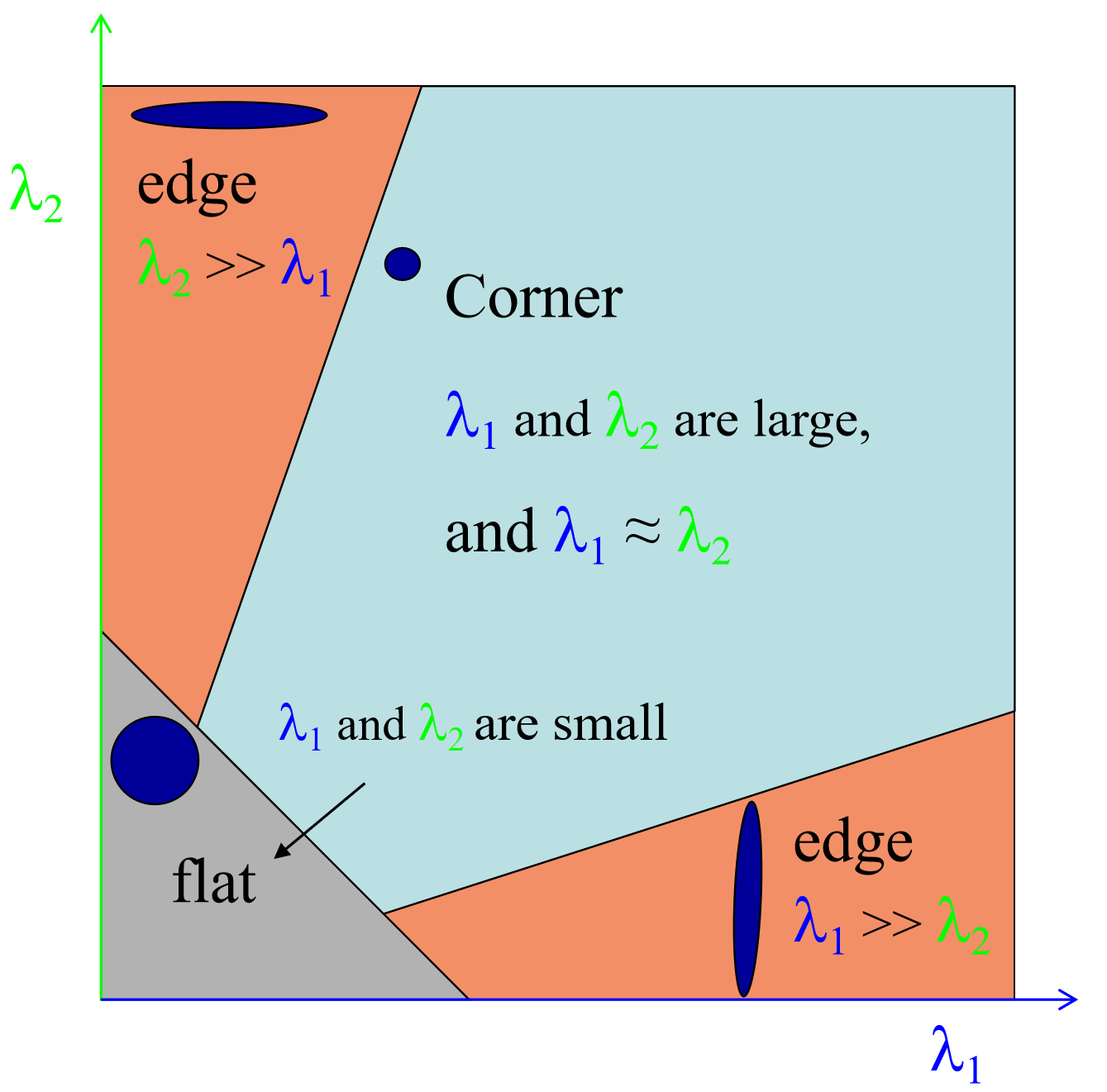
1) |R| 小的区域，即 $\lambda_1$ 和 $\lambda_2$ 都小；

2) ： R <0 的区域，即 $\lambda_1 >> \lambda_2$ 或反之；

3) R 大的区域，即 $\lambda_1$ 和 $\lambda_2$ 都大且近似相等

为了便于直观理解，绘制成 $\lambda_1-\lambda_2$ 平面如下图：

2.3 cornerHarris()

OpenCV 中 Harris 角点检测的函数为:

void  cornerHarris (
    InputArray      src,   // 输入图像 (单通道，8位或浮点型)
    OutputArray     dst,   // 输出图像 (类型 CV_32FC1，大小同 src)
    int      blockSize,    // 邻域大小
    int      ksize,        // Sobel 算子的孔径大小
    double   k,            // 经验参数，取值范围 0.04 ~ 0.06
    int      borderType = BORDER_DEFAULT    // 边界模式
)    　　

2.4 代码示例

#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
 
using namespace cv;
// Harris corner parameters
int  kThresh = 150;
int kBlockSize = 2;
int kApertureSize = 3;
double k = 0.04;
 
int main()
{
    // read image
    Mat src, src_gray;
    src = imread("building.jpg");
    if(src.empty())
        return -1;
    cvtColor(src, src_gray, COLOR_BGR2GRAY);
 
    Mat dst, dst_norm, dst_norm_scaled;
    // Harris corner detect
    cornerHarris(src_gray, dst, kBlockSize, kApertureSize, k);
 
    normalize(dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1);
    convertScaleAbs(dst_norm, dst_norm_scaled);
 
    // draw detected corners
    for(int j=0; j < dst_norm.rows; j++)
    {
        for(int i=0; i<dst_norm.cols;i++)
        {
            if((int)dst_norm.at<float>(j,i) > kThresh)
            {
                circle(src, Point(i, j), 2, Scalar(0,255,0));
            }
        }
    }
 
    imshow("harris corner", src);
    waitKey();
}　　

检测结果：

3 Shi-Tomasi 角点

Shi-Tomasi 角点是 Harris 角点的改进，在多数情况下，其检测效果要优于 Harris。二者的区别在于，Shi-Tomasi 选取 $\lambda_1$ 和 $\lambda_2$ 中的最小值，作为新的角点响应值 $R$

$\qquad R = min(\lambda_1, \lambda_2)$

则相应的 $\lambda_1-\lambda_2$ 平面为：

3.1 goodFeaturesToTrack()

OpenCV 中 Shi-Tomasi 角点检测函数为：

void  goodFeaturesToTrack (     
        InputArray      image,     // 输入图像 (单通道，8位或浮点型32位)
        OutputArray     corners,   // 检测到的角点
        int         maxCorners,    // 最多允许返回的角点数量
        double      qualityLevel,  //  
        double      minDistance,   // 角点间的最小欧拉距离
        InputArray  mask = noArray(), //
        int         blockSize = 3,    //
        bool        useHarrisDetector = false,  //
        double      k = 0.04  // 
    ) 　　

3.2 代码示例

#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
 
using namespace cv;
using namespace std;
 
int kMaxCorners = 1000;
double kQualityLevel = 0.1;
double kMinDistance = 1;
 
int main()
{
    // read image
    Mat src, src_gray;
    src = imread("building.jpg");
    if (src.empty())
        return -1;
 
    cvtColor(src, src_gray, COLOR_BGR2GRAY);
    // Shi-Tomasi corner detect
    vector<Point2f> corners;
    goodFeaturesToTrack(src_gray, corners, kMaxCorners, kQualityLevel, kMinDistance);
 
    // draw and show detected corners
    for (size_t i = 0; i < corners.size(); i++)
    {
        circle(src, corners[i], 2.5, Scalar(0, 255, 0));
    }
    imshow("Shi-Tomasi corner", src);
    waitKey();
}　　

检测结果：

4 角点检测的实现

分析 cornerHarris() 源码，复现计算步骤：Sobel 算子求解 dx 和 dy -> 矩阵 M -> boxFilter -> 每个像素的角点响应值 R，对应 C++ 代码实现如下：

#include <iostream>
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
 
using namespace cv;
using namespace std;
 
int kApertureSize = 3;
int kBlockSize = 2;
double k = 0.04;
int  kThresh = 150;
 
int main()
{
    // read image
    Mat src, src_gray;
    src = imread("chessboard.png");
    if (src.empty())
        return -1;
    cvtColor(src, src_gray, COLOR_BGR2GRAY);
 
　  //  determine scale
    double scale = (double)(1 << (kApertureSize - 1)) * kBlockSize;
    scale *= 255.0;
    scale = 1.0 / scale;
 
    // 1) dx, dy
    Mat Dx, Dy;
    Sobel(src_gray, Dx, CV_32F, 1, 0, kApertureSize, scale);
    Sobel(src_gray, Dy, CV_32F, 0, 1, kApertureSize, scale);
 
    // 2) cov matrix
    Size size = src_gray.size();
    Mat cov(size, CV_32FC3);
    for (int i = 0; i < size.height; i++)
    {
        float* cov_data = cov.ptr<float>(i);
        const float* dxdata = Dx.ptr<float>(i);
        const float* dydata = Dy.ptr<float>(i);
 
        for (int j=0; j < size.width; j++)
        {
            float dx = dxdata[j];
            float dy = dydata[j];
 
            cov_data[j * 3] = dx * dx;
            cov_data[j * 3 + 1] = dx * dy;
            cov_data[j * 3 + 2] = dy * dy;
        }
    }
 
    // 3) box filter
    boxFilter(cov, cov, cov.depth(), Size(kBlockSize, kBlockSize), Point(-1,-1), false);
 
    // 4) R
    Mat dst(size,CV_32FC1);
    Size size_cov = cov.size();
    for (int i = 0; i < size_cov.height; i++)
    {
        const float* ptr_cov = cov.ptr<float>(i);
        float* ptr_dst = dst.ptr<float>(i);
        for (int j=0; j < size_cov.width; j++)
        {
            float a = ptr_cov[j * 3];
            float b = ptr_cov[j * 3 + 1];
            float c = ptr_cov[j * 3 + 2];
            ptr_dst[j] = (float)(a * c - b * b - k * (a + c) * (a + c));
        }
    }
 
#if HARRIS_OPENCV  // compare with cornerHarris()
    cornerHarris(src_gray, dst, kBlockSize, kApertureSize, k);
#endif
     
    // 5) normalization
    Mat dst_norm, dst_norm_scaled;
    normalize(dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1);
    convertScaleAbs(dst_norm, dst_norm_scaled);
 
    // 6) drawing corners
    for (int j = 0; j < dst_norm.rows; j++)
    {
        for (int i = 0; i < dst_norm.cols; i++)
        {
            if ((int)dst_norm.at<float>(j, i) > 150)
            {
                circle(src, Point(i, j), 2, Scalar(0, 255, 0));
            }
        }
    }
    imshow("Harris corner", src);
    waitKey();
}　　

检测结果：将求得的角点响应值 $R$ ，输出 txt 文件，与 cornerHarris() 输出的 $R$ 进行比较，结果几乎完全相同 (只有几处小数点后7位的值不同)

5 亚像素角点

5.1 cornerSubpix()

亚像素角点提取的函数 cornerSubPix()，常用于相机标定中，定义如下：

void  cornerSubPix(
        InputArray          image,  // 输入图象(单通道，8位或浮点型)
        InputOutputArray  corners,  // 亚像素精度的角点坐标
        Size              winSize,  // 搜索窗口尺寸的 1/2
        Size             zeroZone,  //
        TermCriteria     criteria   // 迭代终止准则
)  　　

5.2 代码示例

#include <iostream>
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
 
using namespace cv;
using namespace std;
 
int kMaxCorners = 40;
double kQualityLevel = 0.01;
double kMinDistance = 50;
 
int main()
{
    // read image
    Mat src, src_gray;
    src = imread("chessboard.png");
    if (src.empty())
        return -1;
 
    cvtColor(src, src_gray, COLOR_BGR2GRAY);
    // Shi-Tomasi corner detect
    vector<Point2f> corners;
    goodFeaturesToTrack(src_gray, corners, kMaxCorners, kQualityLevel, kMinDistance);
  
    // draw and show detected corners
    for (size_t i = 0; i < corners.size(); i++)
    {
        circle(src, corners[i], 3, CV_RGB(0, 255, 0));
    }
    imshow("Shi-Tomasi corner", src);
 
    TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 40, 0.001);
    // find corner positions in subpixel
    cornerSubPix(src_gray, corners, Size(5, 5), Size(-1, -1), criteria);    
    for (size_t i = 0; i < corners.size(); i++)
    {
        cout << "Corner[" << i << "]: (" << corners[i].x << "," << corners[i].y << ")" << endl;
    }
    waitKey();
}　　

输入棋盘格5行8列，对应7x4个角点，图像的分辨率为 600*387，则所有角点的理论坐标如下表：

角点的图象坐标值输出如下：

参考

《图像局部不变性特征与描述》第 3 章

Harris 角点

http://www.cse.psu.edu/~rtc12/CSE486/

OpenCV Tutorials / feature2d module / Harris corner detector

OpenCV-Python Tutorials / Feature Detection and Description / Shi-Tomasi Corner Detector & Good Features to Track

OpenCV Tutorials / feature2d module / Detecting corners location in subpixels

posted on 2021-03-11 22:16 飞鸢逐浪阅读(2291) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

公告

昵称：飞鸢逐浪
园龄： 9年1个月
粉丝： 120
关注： 9

+加关注

2025年3月

日

一

二

三

四

五

六

合集

OpenCV 系列(15)

OpenCV 之角点检测

1 检测思路

2 Harris 角点

2.1 泰勒展开

2.2 判别方法

2.3 cornerHarris()

2.4 代码示例

3 Shi-Tomasi 角点

3.1 goodFeaturesToTrack()

3.2 代码示例

4 角点检测的实现

5 亚像素角点

5.1 cornerSubpix()

5.2 代码示例

参考

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论

OpenCV 之 角点检测

1 检测思路

2 Harris 角点

2.1 泰勒展开

2.2 判别方法

2.3 cornerHarris()

2.4 代码示例

3 Shi-Tomasi 角点

3.1 goodFeaturesToTrack()

3.2 代码示例

4 角点检测的实现

5 亚像素角点

5.1 cornerSubpix()

5.2 代码示例

参考

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论

OpenCV 之角点检测