拉格朗日对偶性

拉格朗日对偶性

---

 

在约束最优化问题中，常常利用拉格朗日对偶性（Lagrange duality）将原始问题转为对偶问题，通过解对偶问题而得到原始问题的解。例如，最大熵模型与支持向量机。

 

原始问题

假设f(x)，c_i(x)，h_j(x)是定义在R^_n上的连续可微函数。考虑约束最优化问题，即原始问题：

首先，引进广义拉格朗日函数（generalized Lagrange function）

这里，a_i，β_j是拉格朗日乘子，a_i≥0。考虑x的函数：

这里，下标P表示原始问题。 

假设给定某个x。如果x违反原始问题的约束条件，当存在某个i使得c_i(x)>0，可令a_i→+∞ 或者当存在某个j使得h_j(w)≠0，可令β_j使β_jh_j(x)→+∞，将其余各a_i，β_j均取为0，那么就有：

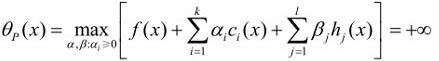也就是：

所以考虑极小化问题  ，即广义拉格朗日函数的极小极大问题，是与原始最优化问题等价的，即它们有相同的解。

为了方便，定义原始问题的最优值  称为原始问题的值。 

对偶问题

广义拉格朗日函数的极大极小问题  ，也可以表示为约束最优化问题：

 

 

称为原始问题的对偶问题。定义对偶问题的最优值  ，称为对偶问题的值。

原始问题和对偶问题的关系 

若原始问题和对偶问题都有最优值，则

证明如下：对任意的a,β和x，有

由于原始问题和对偶问题均有最优值，所以有

得证。

 

在某些条件下，原始问题和对偶问题的最优值相等，d^*＝P^*。这时可以用解对偶问题替代解原始问题。

假设不等式约束c_i(x)是严格可行的，即存在x，对所有i有c_i(x)< 0，则存在x^*,a^*,β^*，使x^*是原始问题的解，a^*,β^*是对偶问题的解，并且  

充分必要条件是x^*,a^*,β^*满足下面的Karush-Kuhn-Tucker(KKT)条件： 

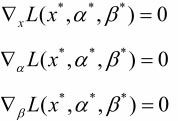
特别指出， 称为KKT的对偶互补条件。由此条件可知：若 a_i^* > 0，则c_i(x^*)＝0。

其实可以简单认为当 c_i(x)=0 时，原始问题和对偶问题的解相等。