机器学习基础——规则化(Regularization) 深入理解计算机系统》(CSAPP)读书笔记 —— 第七章 链接
机器学习基础——规则化(Regularization)
深入理解计算机系统》(CSAPP)读书笔记 —— 第七章 链接
链接( Clinking)是将各种代码和数据片段收集并组合成为一个单一文件的过程,这个文件可被加载(复制)到内存并执行。链接可以执行于编译时( compile time),也就是在源代码被翻译成机器代码时;也可以执行于加载时( load time),也就是在程序被加载器(lad er)加载到内存并执行时;甚至执行于运行时( run time),也就是由应用程序来执行。在早期的计算机系统中,链接是手动执行的。在现代系统中,链接是由叫做链接器( linker)的程序自动执行的
为什么需要了解链接器?
理解链接器将帮助你构造大型程序。构造大型程序的程序员经常会遇到由于缺少模块、缺少库或者不兼容的库版本引起的链接器错误。除非你理解链接器是如何解析引用、什么是库以及链接器是如何使用库来解析引用的,否则这类错误将令你感到迷惑和挫败。
理解链接器将帮助你避免一些危险的编程错误。Linux链接器解析符号引用时所做的决定可以不动声色地影响你程序的正确性。在默认情况下,错误地定义多个全局变量的程序将通过链接器,而不产生任何警告信息。由此得到的程序会产生令人迷惑的运行时行为,而且非常难以调试。我们将向你展示这是如何发生的,以及该如何避免它。
理解链接将帮助你理解语言的作用域规则是如何实现的。例如,全局和局部变量之间的区别是什么?当你定义一个具有 static属性的变量或者函数时,实际到底意味着什么。
理解链接将帮助你理解其他重要的系统概念。链接器产生的可执行目标文件在重要的系统功能中扮演着关键角色,比如加载和运行程序、虚拟内存、分页、内存映射。
理解链接将使你能够利用共享库。多年以来,链接都被认为是相当简单和无趣的然而,随着共享库和动态链接在现代操作系统中重要性的日益加强,链接成为一个复杂的过程,为掌握它的程序员提供了强大的能力。比如,许多软件产品在运行时使用共享库来升级压缩包装的( shrink- wrapped)二进制程序。还有,大多数Web服共享库的动牡动太内
静态链接
像 Linux LD程序这样的静态链接器以一组可重定位目标文件和命令行参数作为输入,生成一个完全链接的、可以加载和运行的可执行目标文件作为输出。输入的可重定位目标文件由各种不同的代码和数据节( section)组成,每一节都是一个连续的字节序列。指令在一节中,初始化了的全局变量在另一节中,而未初始化的变量又在另外节中。
为了构造可执行文件,链接器必须完成两个主要任务:
符号解析( symbol resolution)。目标文件定义和引用符号,每个符号对应于一个函数、一个全局变量或一个静态变量(即C语言中任何以 static属性声明的变量)。符号解析的目的是将每个符号引用正好和一个符号定义关联起来。
重定位( relocation)。编译器和汇编器生成从地址0开始的代码和数据节。链接器通过把每个符号定义与一个内存位置关联起来,从而重定位这些节,然后修改所有对这些符号的引用,使得它们指向这个内存位置。链接器使用汇编器产生的重定位条目( relocation entry)的详细指令,不加甄别地执行这样的重定位。
目标文件
目标文件有三种形式: ** 可重定位目标文件**。包含二进制代码和数据,其形式可以在编译时与其他可重定位目标文件合并起来,创建一个可执行目标文件可执行目标文件。包含二进制代码和数据,其形式可以被直接复制到内存并执行。
可执行目标文件。包含二进制代码和数据,其形式可以被直接复制到内存并执行。
** 共享目标文件**。一种特殊类型的可重定位目标文件,可以在加载或者运行时被动态地加载进内存并链接。
** 编译器和汇编器生成可重定位目标文件(包括共享目标文件)。链接器**生成可执行目标文件。
可重定位目标文件

.text:已编译程序的机器代码。
.rodata:只读数据,比如 printf语句中的格式串和开关语句的跳转表。
.data:已初始化的全局和静态C变量。局部C变量在运行时被保存在栈中,既不出现在,data节中,也不出现在.bss节中
.bss:未初始化的全局和静态C变量,以及所有被初始化为0的全局或静态变量。在目标文件中这个节不占据实际的空间,它仅仅是一个占位符。目标文件格式区分已初始化和未初始化变量是为了空间效率:在目标文件中,未初始化变量不需要占据任何实际的磁盘空间。运行时,在内存中分配这些变量,初始值为0。
.symtab:一个符号表,它存放在程序中定义和引用的函数和全局变量的信息。一些程序员错误地认为必须通过-g选项来编译一个程序,才能得到符号表信息。实际上,每个可重定位目标文件在. symtab中都有一张符号表(除非程序员特意用 STRIP命令去掉它)。然而,和编译器中的符号表不同, symtab符号表不包含局部变量的条目。
.rel.text:一个.text节中位置的列表,当链接器把这个目标文件和其他文件组合时,需要修改这些位置。一般而言,任何调用外部函数或者引用全局变量的指令都需要修改。另一方面,调用本地函数的指令则不需要修改。注意,可执行目标文件中并不需要重定位信息,因此通常省略,除非用户显式地指示链接器包含这些信息。
.rel.data:被模块引用或定义的所有全局变量的重定位信息。一般而言,任何已初始化的全局变量,如果它的初始值是一个全局变量地址或者外部定义函数的地址,都需要被修改。
.debug:一个调试符号表,其条目是程序中定义的局部变量和类型定义,程序中定义和引用的全局变量,以及原始的C源文件。只有以-g选项调用编译器驱动程序时,才会得到这张表。
.line:原始C源程序中的行号和.text节中机器指令之间的映射。只有以-g选项调用编译器驱动程序时,才会得到这张表。
.strtab:一个字符串表,其内容包括. symtab和, debug节中的符号表,以及节头部中的节名字。字符串表就是以nu11结尾的字符串的序列。
符号和符号表
每个可重定位目标模块m都有一个符号表,它包含m定义和引用的符号的信息。在链接器的上下文中,有三种不同的符号:
由模块m定义并能被其他模块引用的全局符号。全局链接器符号对应于非静态的C函数和全局变量。
由其他模块定义并被模块m引用的全局符号。这些符号称为外部符号,对应于在其他模块中定义的非静态C函数和全局变量。
只被模块m定义和引用的局部符号。它们对应于带 static属性的C函数和全局变量。这些符号在模块m中任何位置都可见,但是不能被其他模块引用。
如何解析多重定义的全局符号
链接器的输入是一组可重定位目标模块。每个模块定义一组符号,有些是局部的(只对定义该符号的模块可见),有些是全局的(对其他模块也可见)。如果多个模块定义同名的全局符号,会发生什么呢?下面是 Linux编译系统采用的方法。
在编译时,编译器向汇编器输出每个全局符号,或者是强( strong)或者是弱(weak),而汇编器把这个信息隐含地编码在可重定位目标文件的符号表里。函数和已初始化的全局变量是强符号,未初始化的全局变量是弱符号。 根据强弱符号的定义, Linux链接器使用下面的规则来处理多重定义的符号名
规则1:不允许有多个同名的强符号。
规则2:如果有一个强符号和多个弱符号同名,那么选择强符号。
规则3:如果有多个弱符号同名,那么从这些弱符号中任意选择一个。
重定位
一旦链接器完成了符号解析这一步,就把代码中的每个符号引用和正好一个符号定义(即它的一个输入目标模块中的一个符号表条目)关联起来。此时,链接器就知道它的输入目标模块中的代码节和数据节的确切大小。现在就可以开始重定位步骤了,在这个步骤中,将合并输入模块,并为每个符号分配运行时地址。重定位由两步组成:
重定位节和符号定义。在这一步中,链接器将所有相同类型的节合并为同一类型的新的聚合节。例如,来自所有输入模块的.data节被全部合并成一个节,这个节成为输出的可执行目标文件的.data节。然后,链接器将运行时内存地址赋给新的聚合节,赋给输人模块定义的每个节,以及赋给输人模块定义的每个符号。当这一步完成时,程序中的每条指令和全局变量都有唯一的运行时内存地址了。
重定位节中的符号引用。在这一步中,链接器修改代码节和数据节中对每个符号的引用,使得它们指向正确的运行时地址。要执行这一步,链接器依赖于可重定位目标模块中称为重定位条目( relocation entry)的数据结构,我们接下来将会描述这种数据结构。
加载可执行目标文件
每个 Linux程序都有一个运行时内存映像,类似于图7-15中所示。在 Linux x86-64系统中,代码段总是从地址0x400000处开始,后面是数据段。运行时堆在数据段之后,通过调用malloc库往上增长。堆后面的区域是为共享模块保留的。用户栈总是从最大的合法用户地址()开始,向较小内存地址增长。栈上的区域,从地址开始,是为内核( kernel)中的代码和数据保留的,所谓内核就是操作系统驻留在内存的部分。
为了简洁,我们把堆、数据和代码段画得彼此相邻,并且把栈顶放在了最大的合法用户地址处。实际上,由于.data段有对齐要求,所以代码段和数据段之间是有间隙的。同时,在分配栈、共享库和堆段运行时地址的时候,链接器还会使用地址空间布局随机化。虽然每次程序运行时这些区域的地址都会改变,它们的相对位置是不变的。
当加载器运行时,它创建类似于图7-15所示的内存映像。在程序头部表的引导下,加载器将可执行文件的片( chunk)复制到代码段和数据段。接下来,加载器跳转到程序的入口点,也就是 _start 函数的地址。这个函数是在系统目标文件ctrl.o中定义的,对所有的C程序都是一样的。 _start 函数调用系统启动函数 __libc_start_main,该函数定义在libc.so中。它初始化执行环境,调用用户层的main函数,处理main函数的返回值,并且在需要的时候把控制返回给内核。

总结
链接可以在编译时由静态编译器来完成,也可以在加载时和运行时由动态链接器来完成。链接器处理称为目标文件的二进制文件,它有3种不同的形式:可重定位的、可执行的和共享的。可重定位的目标文件由静态链接器合并成一个可执行的目标文件,它可以加载到内存中并执行。共享目标文件(共享库)是在运行时由动态链接器链接和加载的,或者隐含地在调用程序被加载和开始执行时,或者根据需要在程序调用dlopen库的函数时。
链接器的两个主要任务是符号解析和重定位,符号解析将目标文件中的每个全局符号都绑定到一个唯一的定义,而重定位确定每个符号的最终内存地址,并修改对那些目标的引用。
静态链接器是由像GCC这样的编译驱动程序调用的。它们将多个可重定位目标文件合并成一个单独的可执行目标文件。多个目标文件可以定义相同的符号,而链接器用来悄悄地解析这些多重定义的规则可能在用户程序中引入微妙的错误。
多个目标文件可以被连接到一个单独的静态库中。链接器用库来解析其他目标模块中的符号引用。许多链接器通过从左到右的顺序扫描来解析符号引用,这是另一个引起令人迷惑的链接时错误的来源。
加载器将可执行文件的内容映射到内存,并运行这个程序。链接器还可能生成部分链接的可执行目标文件,这样的文件中有对定义在共享库中的例程和数据的未解析的引用。在加载时,加载器将部分链接的可执行文件映射到内存,然后调用动态链接器,它通过加载共享库和重定位程序中的引用来完成链接任务。
被编译为位置无关代码的共享库可以加载到任何地方,也可以在运行时被多个进程共享。为了加载链接和访问共享库的函数和数据,应用程序也可以在运行时使用动态链接器。
机器学习基础——规则化(Regularization)
在机器学习中,我们一直期望学习一个泛化能力(generalization)强的函数只有泛化能力强的模型才能很好地适用于整个样本空间,才能在新的样本点上表现良好。
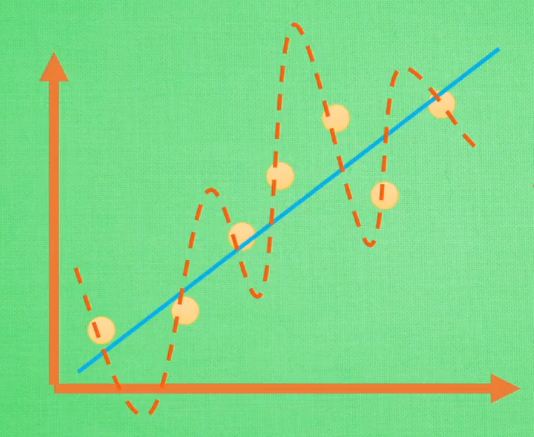
如上图,公式(1)完美地拟合了训练空间中所有的点,如果具备过拟合(overfiting)的能力,那么这个方程肯定是一个比较复杂的非线性函数。正是因为这里的 x2x2 和 x3x3 的参数 cc 和 dd 使得这条曲线可以弯来弯去去拟合训练样本空间中的点。但是我们希望的是模型可以学习到图面中这条蓝色的曲线,因为它能更有效地概括数据,所以我们希望 cc 和 dd 的值相对减小。虽然蓝色函数训练时对应的误差要比红色的大,但它概括起数据来要比蓝色的好。
训练集通常只是整个样本空间很小的一部分,在训练机器学习模型时,稍有不注意,就可能将训练集中样本的特性当作全体样本的共性,以偏概全,而造成过拟合,如何避免过拟合,是机器学习模型时亟待解决的绊脚石。
从问题的根源出发,解决过拟合无非两种途径:
- 使训练集能够尽可能全面的描述整个样本空间。因此又存在两种解决方案。①减少特征维数,特征维数减少了,样本空间的大小也随之减少了,现有数据集对样本空间的描述也就提高了。②增加训练样本数量,试图直接提升对样本空间的描述能力。
- 加入
规则化项。(规则化在有些文档中也称作正规化)
第一种方法的人力成本通常很大,所以在实际中,我们通常采用第二种方法提升模型的泛化能力。
规则化(Regularization)
首先回顾一下,在寻找模型最优参数时,我们通常对损失函数采用梯度下降(gradient descent)算法
通过上述公式,我们将一步步走到损失函数的最低点(不考虑局部最小值和鞍点的情况),这是的 ww 和 bb 就是我们要找的最优参数。
我们可以看到,当我i们的损失函数只考虑最小化训练误差,希望找到的最优函数能够尽可能的拟合训练数据。但是正如我们所了解的,训练集不能代表整个样本空间,所以训练误差也不能代表测试误差,训练误差只是经验风险,我们不能过分依赖这个值。当我们的函数对训练集拟合特别好,训练误差特别小时,我们也就走进了一个极端——过拟合。
为了解决这个问题,研究人员提出了规则化(regularization)方法。通过给模型参数附加一些规则,也就是约束,防止模型过分拟合训练数据。规则化通过在原有损失函数的基础上加入规则化项实现。
此时,最优化的目标函数如下:
其中,第一项对应于模型在训练集上的误差,第二项对应于规则化项。为了使得该目标函数最小,我们需要对训练误差和规则化项之间做出权衡。
那应该选择怎样的表达式作为规则化项呢?以下引用李航博士《统计学习方法》中的一些描述:
规则化是结构风险最小化策略的实现,是在经验风险最小化上加一个规则化项(regularizer)或惩罚项(penalty term)。规则化项一般是模型复杂度的单调递增函数,模型越复杂,规则化值就越大。比如,规则化项可以是模型参数向量的范数。
规则化符合奥卡姆剃刀(Occam‘s razor)原理。奥卡姆剃刀原理应用于模型选择时变为以下想法:在所有可能选择的模型中,能够很好地解释已知数据并且十分简单才是最好的模型,也就是应该选择的模型。从贝叶斯估计的角度来看,规则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率,简单的模型有较小的先验概率。
我们通常采用L1-范数和L2-范数作为规则化项。
L-1范数
向量的L1-范数是向量的元素绝对值之和,即
当采用L1-范数作为规则化项对参数进行约束时,我们的优化问题就可以写成一下形式:
采用拉格朗日乘子法可以将约束条件合并到最优化函数中,即
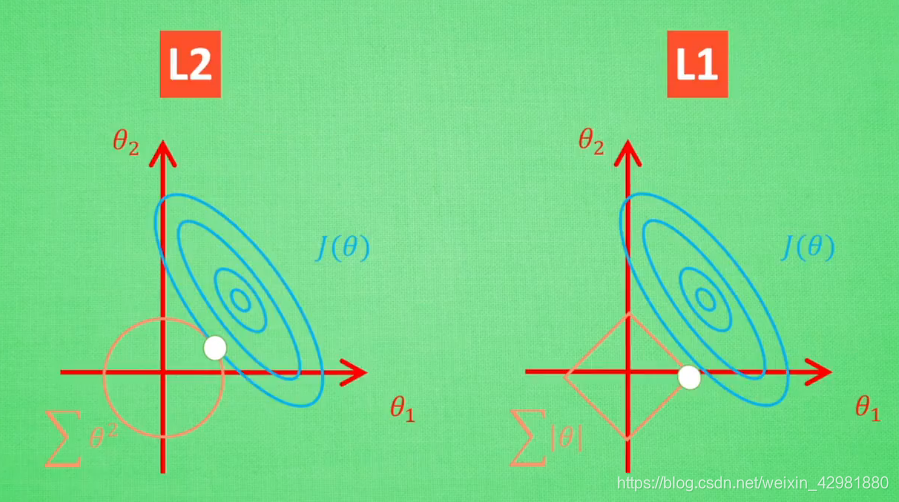
其中,λλ 是与 CC 一一对应的常数,用来权衡误差项和规则化项,λλ 越大,约束越强。二维情况下分别将损失函数的等高线图和L1-范数规则化约束画在同一个坐标轴下,
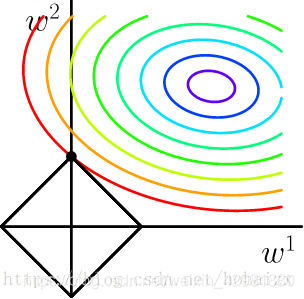
L1-范数在 x=0x=0 处存在拐点,所以不能直接求得解析解,需要用次梯度方法处理不可导的凸函数。
L2-范数
除了L1-范数,还有一种广泛使用的规则化范数:L2-范数。向量的L2-范数是向量的模长,即
当采用L2-范数作为规则化项对参数进行约束时,我们的优化问题可以写成以下形式:
同样可以将约束条件合并到最优化函数中,得到如下函数
也将损失函数的等高线图和L2-范数规则化约束画在同一坐标轴下,
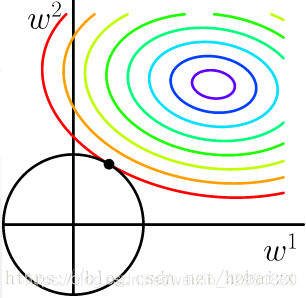
加入L2-范数规则化项后,目标函数扩展为如下形式:
L1-范数和L2-范数的比较
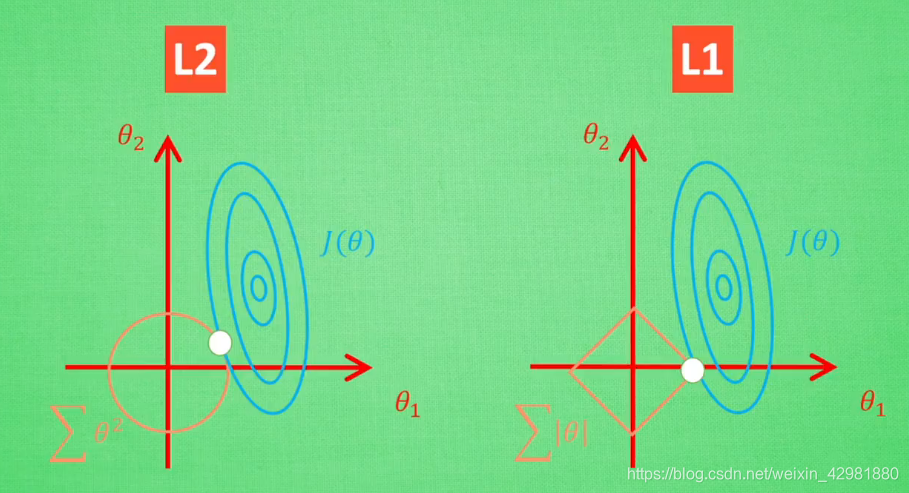
值得一提的是,使用L1-范数的方法很有可能只有 θ1θ1 的特征被保留,所以很多人采用L1-范数规则化提取对结果`贡献最大`的特征。
但是L1的解并不是很稳定,比如批数据训练,每一次批数据都会有稍稍不同的误差曲线。L2对于这种变化,交点的移动并不会特别明显,而L1的交点的很可能会跳到很多不同的地方,如下图。因为这些地方的总误差都差不多,侧面说明了L1的解不稳定。
参考
[1] https://blog.csdn.net/hohaizx/article/details/80973738.
[2] https://www.bilibili.com/video/BV1Tx411j7tJ?from=search&seid=5329920308199944586.



