Scyther-Semantics and verification of Security Protocol 翻译 (第二章 2.2.2----2.3)
2.2.2 事件顺序
协议中的每个角色对应于事件列表,换句话说, 在属于角色 R 的协议事件集上施加结构,总的排序表示为 $ \prec $ , 如此任何角色 R∈Role 和 $\varepsilon 1$ ,$\varepsilon 2$ ∈ RoleEvent,这样 Role($\varepsilon 1$)=R 和 role($\varepsilon 2$)=R 我们有 这样的表达:$ \varepsilon 1 \prec \varepsilon 2\vee \varepsilon 1=\varepsilon 2\vee \varepsilon 1\succ R\varepsilon 2$ 我们认为一个抽象安全协议P 视为通信顺序过程的集合。每一个顺序组件由特定的角色承载。通信由装饰事件的标签管理,因为标签直接决定了通信的关系 ↝。
定义2.10 (通信关系): 所有的 $\imath $∈Label , m1, m2 ∈ Role ×Role ×RoleTerm , 通信关系 ↝ 表示为 :
$\varepsilon 1$ ↝ $\varepsilon 2\Leftrightarrow \exists \imath $ m1,m2:$\varepsilon 1=send \imath (m1) \Lambda \varepsilon 2=read \imath (m2)$ . 该关系规定了发送协议事件和协议接受事件如何对应,
例子: 2.1.1 (事件角色和 通信关系): 比方说 NS 协议, 角色顺序 $\prec$ i 和 $\prec$ r 是角色 i 和 r ,分别如下表示:
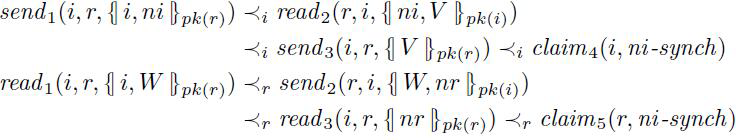
通信关系 ↝ 给出如下表示:

2.2.3 静态要求
在之前的章节中我么解释了抽象的协议规范语法。适当的协议规范必须满足许多良好的形式要求,并不是任何发送、声明、读取事件序列被认为是安全的协议,比方说,我们要求代理必须能够构建他发出的术语条款,如果他不知道秘钥则不能检查加密术语的内容。
良好的角色: 对于每一个角色,我么要求他符合基本的某些标准,这些范围相当的明显,例如:角色定义中的每个事件都具有相同的角色执行它(被称为该事件的参与者),关于消息的更加微小的要求。对于消息,我们要求发着的消息实际上可以有发送者构造,如果消息在发送角色中,则满足此要求。对于变量我们要求首先出现在一个读取事件中, 在该事件中被实力化,然后才能出现在发送事件中。
对于读取事件,情况要复杂的多,从上面的列子中可以看出,我们描述协议 Needham-Schroeder 初始角色,读取事件对传入的消息施加结构,以这种模式的形式,如果接受者的知识满足某些要求,那么他只能将消息与这种预期的模式相匹配。
我们介绍一种预测形式 WF (Well- Formed) 表示角色定义满足这些一致性要求,使用辅助预测 RD (Readable)和一个推论知识关系$ \vdash $ : RoleKnow × RoleTerm
角色可以组成和分解术语对,如果代理知道加密秘钥则可以加密术语,如果代理知道解密秘钥则同样可以解密加密的术语。
定义 2.12 (知识推理操作)
使用 M 作为角色知识集,知识推理关系$ \vdash $ : RoleKnow × RoleTerm 定义归纳如下: 针对所欲的角色术语 rt 、 rt1 、 rt2 、k
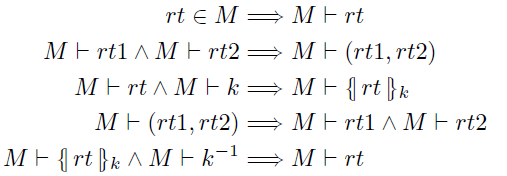
列子 2.13 (推理和加密)
从一个包含 {/m/}k术语的术语集,不包含$k^{-1}$ 不能够推断出 m 或者 k ,i ,e
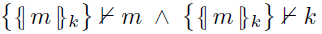
给定术语表达式 {/m/}k 和 $k^{-1}$ ,我们能够推断 m , 如果 k 是非对称秘钥(这就是说 k 不等于$k^{-1}$ ),给定{/m/}k 和 $k^{-1}$ 不可能推断 k
例子 2.14 (推论和子项):给定两个术语 m1 和 m2 关系是 {m1}$\vdash $m2 ,通常并不是这种 m2$ \sqsubseteq $ m1 ,给出一个反例: m1 =( rt1, rt2) 和 m2=(rt2, rt1) 当 rt1不等于 rt2的时候。反过来也没有。例如 因为给定术语 k 和 m 以及 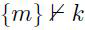 ,我们有 k $\sqsubseteq $ {/m/}k 还有
,我们有 k $\sqsubseteq $ {/m/}k 还有
例子 2.15 (推论和函数)给定术语 f(rt) 且 f ∈Func , 没有适用的进一步推理规则,如此推断 rt 是不可能的,在这方面,我们框架中的函数充当散列函数。我们可以放心的安全建模秘钥 (列如:k(rt1,rt2),sk(rt1)) 作为散列函数在相同的地方。正如我们后面将看到的,代理名称最初被代理和入侵者所知。建模 , 因此不会增加任何相关方的可推断条款。
, 因此不会增加任何相关方的可推断条款。
(在模型中,应用推理运算符的所有集合都包括 rt1 、 rt2)
预测 RD: P(RoleTerm)× RoleTerm 表示哪些角色术语可以用作具有特定知识集的代理读取事件的消息模式。变量总会在读取模型中出现,其他任何术语只能以读取模式发生,如果可以从代理的知识中推断出来(由从任何先前读取事件中获得的初始知识组成),只有这样才能将它与传入的消息进行比较。
为了能够读取整对,我们必须读取每个成分,同时通过从其他组件推断出的知识扩展知识,如果可从知识推断出加密消息,或者如果可以在解密之后推断出加密消息,则可以读取加密消息。
定义 2.16 (可读预测):M 是 一个角色知识集,rt 是一个角色术语, 用作下面的额模式。

特殊的,如果看到这种情况, rt $\equiv $(rt1 , rt2) 能够读取这样的消息可以对应于首次从 rt2 提取一些秘钥,该秘钥可以用于解密 rt1 。反之也成立。
我们有这样新的预测结构, WF:Role × RoleSpec ,表示角色形式很好, 此预测第一个参数始终是事件发生角色,它用于表示执行事件的角色(例如:发送事件的发送者)应该与发生的角色相匹配,从发送和声明事件知识中必须可以推断出术语。而读取事件中的发生术语不许根据上述定义可读。此外,代理应该只能读取指向他的信息,并且只能发送给标记正确标签的消息。如果一个术语在一个声明事件中作为i参数,没有这样的要求,因为这取决于声明事件中参数的功能,在后续的章节中将会看到。
定义 2.17 (好的构造性): R是一个 角色,M 作为一个角色知识集,让我们列出角色事件列表:
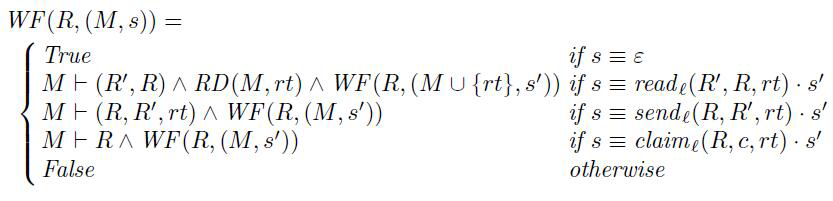
对于协议规范 P: Role $\mapsto$RoelSpec 我们要求所有的角色都是关于最初的知识良好的形式。表示为 $\forall R\epsilon $dom(P): WF (R,P(R)) , 我们使用 dom(f) 表示 f 的部分功能。
例子 2.18 (角色描述的正确性): 首先考虑下面不正确的角色描述:
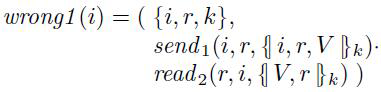
角色描述 wrong1 格式错误,因为在读取时发送变量 V。根据定义 2.6 初始角色知识集不包含变量,在 WF预测形式中,变量将会只会成为角色知识的一部分(参数 M)在他们已经读取后。在随后的事件中 这些变量可以从 m 中推断出来,因此可以作为发送消息的一部分。
例子 2.19 (正确的角色描述) :考虑下面错误的角色描述:
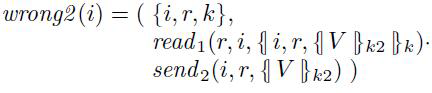
我们看到在 wrong2 中的读事件 包含一个 子术语 {/ V/}k2 ,目的是通过此读取初始化 V。 然而 k2 是对称秘钥, k2 不是角色知识,通过此读无法确定V的值。因此角色描述格式不正确,正确的角色描述如下:
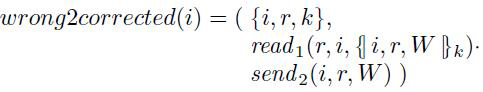
2.3 协议执行描述
在上面的章节中我们已经成了协议形式化的描述概念,是协议如何表现的静态描述,当这样的协议描述执行的时候,动态方面介绍,涉及到代理模型的各个方面以及域分析的执行模型,这就需要引入一些协议描述级别上没有出现的新概念。特别的我们将模拟的动态行为建模为标记过度系统。
2.3.1 运行
协议规范描述了一组角色,这些角色充当系统中实际代理可以执行的操作蓝图,执行协议时,每个角色可以执行多次运行,可能是并行执行,也可由多个代理执行。我们称之为一个单 (运行)可能是部分的,执行一个角色描述为一个运行,从实施角度来看,一个运行 类似于一个线程,在我们的模型中,有同一个代理执行的运行时独立的,不存在共享任何变量问题。
执行角色会将角色描述转换成为运行,这被称为是实例化,为了实例化一个角色,我们必须将角色名称绑定到实际代理的名称上,我们必须使每个实例化的本地常量都是唯一的。此外,我们必须考虑到值与变量的绑定也是运行本地的。因此,在运行中出现的术语集不同于角色描述中出现的术语集。
我们假设存在一个集合 RID 来表示运行表示符, 并设置一个代理集合表示 代理,运行术语和角色术语定义是类似的,不同之处在于抽象角色由具体代理替换,通过使用运行标识符扩展局部常量使其成为唯一的。运行术语集好包括由入侵者生成的基本的集合 IntruderConst ,这个集合只会在2.4.2 章节中使用, 以后会再详细的介绍。
定义 2.20 (运行术语)并且变量由具体值实例化,

定义 2.21 (实例功能): 对于每一个运行, 存在两个两个相关的角色术语和运行术语,一个角色术语转换成一个运行术语,
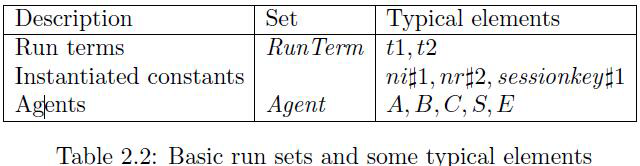
通过应用实例化:

实例化的第一个组件确定常量扩展的运行标识符,第二个组件确定代理的角色实例化。第三个决定了变量的估值。
我们延伸 逆 function$^{-1}$ 到运行术语集中,角色功能: RoleTerm $\rightarrow $P(Role)和 vars: RoelTerm$\rightarrow $P(Var) 确定术语中出现的角色和变量,我们以明显的方式将这些功能扩展到RoleSpec。
我们经常提取第一个组件,运行标识符来自实例化。我们将使用符号 runidof(inst) 表示运行标识符来自实例化 inst
定义 2.22 (实例化术语)
我们有 inst∈Inst 是一个实例,而 inst=(θ,ρ,σ) ,使 f ∈ Func 和 rt 、rt1....... rtn 作为角色术语,像这样 roles(rt) $\subseteq$dom(ρ) 和 vars(rt)$\subseteq$dom(σ), 我们定义实例:<inst>:
RoleTerm $\rightarrow $RunTerm 如下:
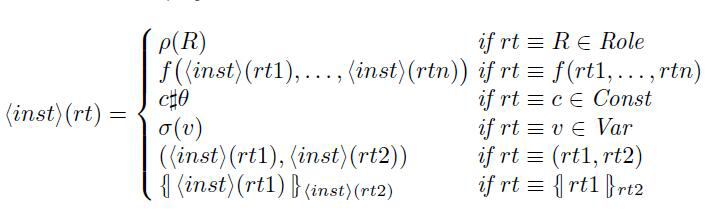
例子 2.23 (实例化术语) 我们改定两个实例化,可能在执行协议的时候发生:

定义 2.24 (运行) 一个运行是事件角色的实例化,定义为 Run=Inst ×RoleEvent$^{x}$
我们将会在后面看到,每一个系统的运行,将会有一个确定的标识符,因为通过角色描述已经实现了静态定义, 我们可以在运行规范中省略他。
考虑到系统由一些代理执行的许多运行组成,运行之间的通信是异步的。为了方便模拟不同入侵者的行为,我们将通信通过两个缓冲。我们有一个输出缓存来自发送运行,还有有个输入缓存来自接受运行。(关于这种)入侵者能够决定消息从输出缓存到输入缓存。输出缓存和输入缓存都可以存储消息,消息包括发送者、接受者。一个运行的术语表达式: MSG=Agent × Agent × RunTerm 。 缓冲区是这样消息的多重集合 : Buffer=M(MSG) ,为了避免标记混乱,我么使用MSG 当 MSG∈ RunTerm ,避免在RunTerm 上重定义已经存在的操作
完整的网络模型还包括入侵者元素,目前还没有讨论过,特别的,在过度系统中定义状态概念,我们需要介绍一组术语从 P(RunTerm),在第2.4 节中提到过动入侵的概念。
定义 2.25 (网络状态): 在一个安全协议中,代理执行角色的网络状态定义如下:
State=P(RunTerm)× Buffer × Buffer × P (Run) 这样状态中包含攻击者知识,内容有输出缓存,输入缓存,(而且剩余的)任然要被执行。
指定在读取事件中,如果匹配确定的模式,来自缓冲区的消息会被代理接受,我么引入一种预测模型 Match 表示消息与变量的某些实例化模型匹配。这个预测的定义知识系统的一个参数,我们将会给出一个直接的匹配实例。
例如,我们为每个变量定义一组允许值得运行术语,我么介绍一种辅助函数类型 : Var -----P(RunTerm ) :定义作为变量有效值的运行术语集。我们可以给出三个定义类型的列子,会导致读取事件的语义有稍微的不同。
例子 2.26 (模型匹配: 武缺陷类型): 在大多数情况下,我们假设运行术语集被划分成有限的 S1、 S2、 ..... Sn ,这可以代表代理角色,随机变量、代理名称、会话秘钥、加密、元组。这种类型匹配模型我们有下面的要求,
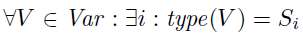 如果变量的类型是 Nonce ,仅仅匹配运行术语的 Nonce
如果变量的类型是 Nonce ,仅仅匹配运行术语的 Nonce
定义 2.27 (简单类型匹配:基础类型缺陷):



