Scyther-Semantics and verification of Security Protocol
1 、本书前一节主要是介作者自己的生平经历(读完感觉作者是个神童),目标明确作者13岁代码已经写的很溜了。自己也开了网络公司,但是后面又专注于自己的计算机基础理论,修了哲学的博士学位(不得不说很多专业的交叉真的可以创造新的起点),但是任何领域的开辟都是来自自己不辞辛苦的决心和坚韧不拔的毅力。
本来之前一直是在看渗透测试的方面资料,但是后面加上实习的事,论文View“”被“”选择成工业网络协议的形式化分析,没有人指导该怎么去做,迷茫应该往哪个方向上分析,先是对EtherNet/IP 协议ODVA发布的规范文档的阅读,(刚开始看的的时候感觉看不到头,没有自己期望的相关资料或者越看越复杂)就好像一棵藤,自己独自摸索着向前,每一个枝节会有新的问题或者概念蹦出,然后在返回去找相关的资料。(这种情况像是叠罗汉),但是这中间我感觉自己走了很多弯路(磕磕碰碰),因为急切的想要找到期望的,切中要点的idea ,这样我就很多时候半途而废(太摧残),就像漫画上一个人挖井,挖到一般看不到希望就放弃另寻锚点挖。有个之前寻求帮助的博士说“你四处询问的所需要的东西往往就在你眼前”所以真的要静下心来,坚持下去。就是觉得自己在计算机方面的能力真的有待提高,所以尴尬的近况就是真的害怕自己做不出来,现在还有论文方面还存在两个困难。
一是EtherNet/IP协议中应用层CIP协议中使用的安全传输机制TLS协议和DTLS协议自身的问题(TLS1.3版本已经更新,但是ODVA中的支持的芯片未来3-6年才能更新支持),如果对EtherNet/IP协议形式化分析,拿现有的TLS1.2作为分析,还是使用TLS1.3,1.3的版本在协议内容上存在较大的改变。但是如果使用TLS1.3做形式化分析,本身CIP中的所有密码套件不支持,在回溯到EtherNet/IP 协议的自身安全的时候就会无法进行下去。考虑到此所以对CIP协议分析的采用目前使用的TLS1.2版本,分析完之后对其中的漏洞和安全问题以及攻击路径做整理回溯到CIP安全,在回溯到EtherNet/IP协议的安全,这里加上比较TLS1.2和TLS1.3存在的差异,(后面扩展视时间而定)。
二是Scyther 形式化分析工具的手册和语义分析的资料书目前还是没有看懂,Scyther user manual 已经看完,但是由于里面的内容是基于Scyther-Semantics and verification of Security Protocol 的,所以必须先吃透这本书的内容。
现在第一个问题具体部署完成,预计周末完成比较和分析的梳理。现在对第二个问题进行分篇章的整理。
2、Scyther-Semantics and verification of Security Protocol(整理)
内容:
第一节:Dolev-Yao模型 (假设基础, 要分析的密码算法是完美的,消息是抽象的术语,网络完全可由入侵者控制)
安全模型的术语定义: 首先安全协议区分了很多行为,每个这样的协议行为成为角色,
协议规范描述了协议中的每个角色的行为,将协议规范视为语义的参数,定义抽象的语法制定安全协议,将安全协议中的角色指定为一系列的事件,挑战响应机制(通常成为Nonce 随机数)或者会话秘钥,在整个协议中有重要的作用,按照协议提出一个抽象的语法和静态要求,代理模型:代理执行协议的角色,可以并行执行多次,是封闭的假设(诚实的代理不会对外泄露分类消息),代理模型描述了如何解释角色的运行,代理按照顺序执行角色的描述,等待读取时间,
通信模型:通信模型描述了消息之间的关系代理商的交换,我们选择异步模型通讯。使用缓冲区(暂)
威胁模型: 参见 Dolev-Yao
密码 原语: 密码原语是理想化的数学结构,例如加密,在对加密原语的处理中,使用了所谓黑盒测试,只是知道密码算法的相关属性,只考虑非对称和对称算法,并且假设要分析的协议使完美的。
本章使用NS协议(Needham-Scroeder),使用消息序列图(MSC)来说明安全协议的攻击: 首先 发起者 i 拥有公钥pk(r)和私钥sk(i) ,同时接受者也同样拥有公钥pk(i)和私钥sk(r) ,发起者向接受者发送个个随机变量 ni 同时加上自己的身份 i ,使用 公钥 pk(r)进行加密,接受者 r 接收到消息之后向发送者发送一个随机变量 nr 加上之前的随机变量 ni 使用自己的公钥 pk(i)进行加密。接受者收到消息之后,解密出nr 发送给 接受者,并使用自己的公钥进pk(r)行加密,这样发送者和接受者都声称自己有安全认证的属性 ni-synch 的拥有者。

角色术语: 定义基本的角色术语
Var : 表示用于存储接受消息的变量 、 Const :表示角色的每个实例化新生成的常量,被认为是局部常量。 、 Role :定义角色 、 Func :表示函数的名字
我们将角色术语集定义为基本术语套,使用构造函数进行扩展以进行配对和加密,并且假设配对是右关联的。
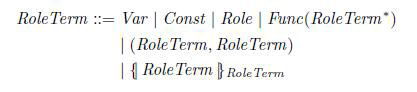
当我们想要使用个函数的 f 的时候,其定义域是 X,可以这样标记 :-------> {f(x)| x ∈X}
这里我们定义一个术语的逆 使用函数:
 我们规定 — -1是自己的逆, (rt -1)-1=rt
我们规定 — -1是自己的逆, (rt -1)-1=rt
在整片论文中我们假设公钥pk 和私钥映射到非对称秘钥的元素函数中,我们使用pk 表示i代理的公钥,使用sk表示代理的私钥
(补充数学量词 ∀R∈Role :pk(R)-1=sk(R)^sk(R)-1=pk(R) 表示 对任意的R 属于 Role均成立右面的等式。)
例子: 我们建立角色R的私钥模型 sk(R)和对应公钥的逆 pk(R),使用公钥模型加密消息 m 表示模型为 : {/m/}pk(R) , 对消息进行签名,并不是直接使用秘钥进行加密,而是被称为:消息摘要”加密,
为了使私钥正确的签名消息 m 模型,我们需要一个函数 h , 签署消息 m 之后的的术语是 (m, {/h(m)/}sk(R))
定义:描述角色,(协议是由角色组成的,而角色又是由角色事件组成的)。
我们定义一组事件集,RoleEvent 使用两个新的组,标签 Labe 和安全声称 Claims
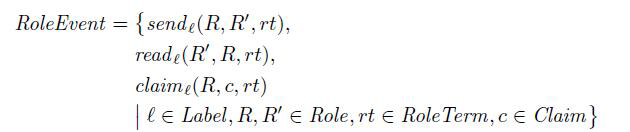
上面的事件集解释如下: 事件 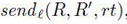 表示发送的消息 rt 绑定到代理 R上 ,打算用于绑定代理 R' ,同样的
表示发送的消息 rt 绑定到代理 R上 ,打算用于绑定代理 R' ,同样的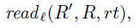 指明消息 rt 被代理 R ’ 绑定,显然是由代理 R发送过来的,事假声明
指明消息 rt 被代理 R ’ 绑定,显然是由代理 R发送过来的,事假声明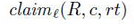 表达,执行此事件时 R 期望安全目标 c 与可选参数 rt 保持一致。声称事件仅仅表示涉及本地代理R 并不是其他任何人的期望的代理。标签
表达,执行此事件时 R 期望安全目标 c 与可选参数 rt 保持一致。声称事件仅仅表示涉及本地代理R 并不是其他任何人的期望的代理。标签 标记事件来消除协议规范中相同事件的类似避免发生歧义,第二层含义是表达发送事件和接受事件的之间的关系,
标记事件来消除协议规范中相同事件的类似避免发生歧义,第二层含义是表达发送事件和接受事件的之间的关系,
定义次运算符: 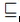 定义子术语,其中包括用于加密的秘钥,注意术语形如 f(rt)的术语没有子句,因为被认为是非组合型术语。除了发送和接受术语之外,角色规范还定义了执行角色的初始知识,也是一组术语。
定义子术语,其中包括用于加密的秘钥,注意术语形如 f(rt)的术语没有子句,因为被认为是非组合型术语。除了发送和接受术语之外,角色规范还定义了执行角色的初始知识,也是一组术语。
定义如下:
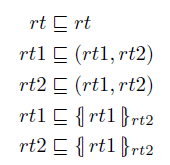
定义 角色知识: 我们定义角色知识,将角色知识集RoleKnow定义为不包含变量作为子项的所有角色术语的集合。
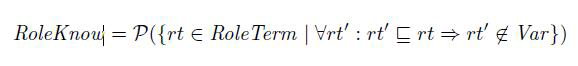 作为结果,我们有这样的表达式
作为结果,我们有这样的表达式  因为角色事件完全描述角色的行为。 没有必要声明局部常量和变量,协议的执行不需要角色知识,这里引入角色知识有两个原因,首先他允许静态角色的一致性测试,在给定初始知识集的情况下查看角色是否可以执行,第二,他将使我们能够系统的推导出文章末尾的初始入侵者。
因为角色事件完全描述角色的行为。 没有必要声明局部常量和变量,协议的执行不需要角色知识,这里引入角色知识有两个原因,首先他允许静态角色的一致性测试,在给定初始知识集的情况下查看角色是否可以执行,第二,他将使我们能够系统的推导出文章末尾的初始入侵者。
定义角色规范: 角色规范包含一系列的事件,一些事初步知识,因此我们定义了角色规范集合 像 : RoleSpec=RoleKnow×RoleEvent*
我们写成[ε1,ε2]指定 两个事件列表,ε1和ε2 ,我们写 [ε1,ε2].[ε3] 去指定两个列表的级联, 经常在书写单个事假的时候我们会省略括号直接写成,ε1.ε2 表示 [ε1,ε2]。
我们书写 A  B指定一个局部函数,他将A的元素映射到元素B上,
B指定一个局部函数,他将A的元素映射到元素B上,
定义2.8 一个协议规范角色行为通过设置协议的部分功能,如此我们有这样的表达式 : Protocol=Role RoleSpec
RoleSpec
我们使用 MRP(R)作为协议规范 P中角色 R的初始知识简写。在很多情况下我们省略 参数 P 在协议上下文很清楚的情况之下。符号 MR是M的缩写,之后我们将用作表示知识,R 用作表示角色。
角色事件在协议中的描述必须是唯一的,可以通过标签事件进行强制执行,者允许我们定义一个角色函数: RoleEvent ------> Role ,鉴于角色事件,角色函数也是事件中的一个。我们将协议作为一个隐式的参数,当协议上下文清楚的时候。
定义 2.9 下面的角色描述模拟了NeedHam-Schroeder 协议的发起者角色,没有任何的安全要求。

2.2.2 事件顺序
事件的每个角色对应于事件列表,换句话说, 一个结构顺序加到属于角色R的协议事件中,这个总数的排序指定  ,如此 对于任何角色R∈Role 和 ε1,ε2 ∈RoleEvent ,这样 role(ε1)=R 和role(ε2)=R 我么有这样的表达式 :
,如此 对于任何角色R∈Role 和 ε1,ε2 ∈RoleEvent ,这样 role(ε1)=R 和role(ε2)=R 我么有这样的表达式 :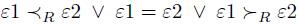 我么认为有个抽象的安全协议 P作为通信序列结合,每一个顺序组件由特定的角色承担。通信由装饰事件的标签管理,标签直接定义沟通(通信)关系:
我么认为有个抽象的安全协议 P作为通信序列结合,每一个顺序组件由特定的角色承担。通信由装饰事件的标签管理,标签直接定义沟通(通信)关系: 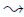
定义2.10 通信关联
对于所有的 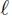 ∈ Label 以及 m1 ,m2 ∈ Role ×Role ×RoleTerm ,通信关系
∈ Label 以及 m1 ,m2 ∈ Role ×Role ×RoleTerm ,通信关系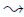 定义为:
定义为: 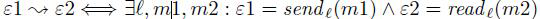 这个关系规范了发送事假和接受事件如何对应。
这个关系规范了发送事假和接受事件如何对应。
Example 2.11 事假顺序和通信关系: 对于示例协议 NS 角色排序 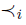 和
和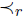 关于角色 i 和 r ,分别表示如下:
关于角色 i 和 r ,分别表示如下:

通信关系表示如下:
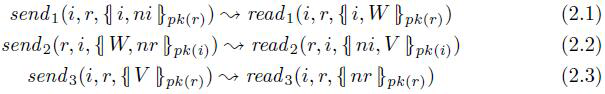
2.2.3 静态要求
在上一节中我们已经解释了协议规范的抽象的语法,适当的协议规范还应当满足很多完好性的要求,并不是任何有发送、接受、和声明的事件被认为是安全的协议,列如,我们要求代理能够构建出他发送的条款,并且他不能检查条款的内容和加密的秘钥。
良好的角色, 对于每一个角色,我们要求有自己确定的标准,这些标注的范围是相当明确的,列如,协议角色定义中的每个时间都是具有执行它的相同的角色(事件参与者和执行者),对于消息,我们要求发送者能够实际构造这些消息,对于变量应该首先出现在接受事件中,在实例化之前可以出现在发送时间中。对于接受事件,从上的协议的列子中可以看出, 在我们描述Needham-Schroeder protocol
我们定义一个 预测 WF 表达一个角色定可以的一致性要求, 使用辅助定义RD (可读性)和一个推理知识的关系,
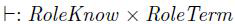 角色可以撰写和分解术语对,如果代理指导加密秘钥,则可以加密术语,如果代理知道响应的解密秘钥,则可以解密加密的术语。
角色可以撰写和分解术语对,如果代理指导加密秘钥,则可以加密术语,如果代理知道响应的解密秘钥,则可以解密加密的术语。
定义 2.12 推理运算法
使用M作为 一个角色知识集, 知识推理关系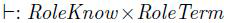 归纳如下: 所有的角色术语 rt ,rt1 ,rt2 ,k :
归纳如下: 所有的角色术语 rt ,rt1 ,rt2 ,k :

Example 2.13 推理和加密 从术语集 组成 术语 term{/m/}k ,但是不是 k -1 无法推断 是m 或者 k i e
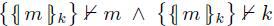 给定
给定 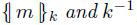 和 k -1 我们能够推断出 m , 如果 k 是非对称秘钥 (如此 k
和 k -1 我们能够推断出 m , 如果 k 是非对称秘钥 (如此 k  k -1 ),并且给定{/m/}k 和k -1 无法推断 K
k -1 ),并且给定{/m/}k 和k -1 无法推断 K
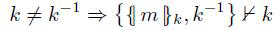
Example 2,1,4 推断和子句
给定术语 m1 和m2 以及  一般情况之下,m2 不是
一般情况之下,m2 不是 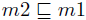 ,一个反例给出 m1=(rt1, rt2) 和 m2=(rt2 ,rt 1) 当 rt 1不等于rt2 ,反之则不然。比如,因为给定术语 k 和 m 以及
,一个反例给出 m1=(rt1, rt2) 和 m2=(rt2 ,rt 1) 当 rt 1不等于rt2 ,反之则不然。比如,因为给定术语 k 和 m 以及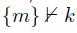 我们有 k
我们有 k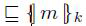 但是
但是
Example 2.1.5 推断和函数



 浙公网安备 33010602011771号
浙公网安备 33010602011771号