九度 1343：城际公路网(最短路径变形)

题目描述：

为了加快城市之间的通行和物资流动速度，A国政府决定在其境内的N个大中型城市之间，增加修建K条公路。已知这N个城市中的任意两个都能相互连通，且已知其最短的路径长度。为了时刻监测修建新路对A国城市的影响，特任命你为观察员，负责在每修建完一条公路之后，就向该国领导汇报当前N个城市间的最短路之和。

 

思路

1. 这道题目是 floyd 算法的变形, 题目已给出任意两个城市之间的最短距离, 每次增加一条道路, 求解增加这条道路后各个城市之间的最短路径之和减小到多少

 

2. floyd 算法描述如下

Floyd-Warshall算法的原理是动态规划

设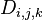为从到的只以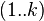集合中的节点为中间节点的最短路径的长度。

1. 若最短路径经过点k，则；
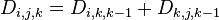2. 若最短路径不经过点k，则。

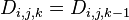因此，。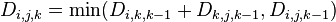

在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维

for k ← 1 to n do
  for i ← 1 to n do
    for j ← 1 to n do
      if (D_{i,k} + D_{k,j} < D_{i,j}) then
        D_{i,j} ← D_{i,k} + D_{k,j};

 

3. 算法初始化时, 最好设置 dp[i][i] = 0, 这样能够省去判断

易错点: i, j 都是从 1 开始, j 并不是从 i+1 开始

 

4. 各个城市之间的最短路径为

int sum() {
    int res = 0;
        for(int i = 1; i <= n; i ++)
            for(int j = i+1; j <= n; j ++)
                res += dist[i][j];
    return res;
} 

 

代码

#include <iostream>
#include <stdio.h>
using namespace std;

const int INF = 0X3F3F3F3F;
int dist[400][400];

int n, k;

int sum() {
    int res = 0;
        for(int i = 1; i <= n; i ++)
            for(int j = i+1; j <= n; j ++)
                res += dist[i][j];
    return res;
} 

int main() {
    freopen("testcase.txt", "r", stdin);
    while(scanf("%d", &n) != EOF) {
        for(int i = 1; i <= n; i ++) {
            for(int j = 1; j <= n; j ++) {
                scanf("%d", &dist[i][j]);
            }
        }

        

        scanf("%d", &k);
        int fm, to, d;
        
        for(int i = 0; i < k; i ++) {
            scanf("%d%d%d", &fm, &to, &d);

            for(int a = 1; a <= n; a ++) {
                for(int b = 1; b <= n; b ++) {                    // WA
                    if(d+dist[a][fm]+dist[to][b] < dist[a][b]) {
                        dist[a][b] = d+dist[a][fm]+dist[to][b];
                        dist[b][a] = dist[a][b];                // WA
                    }
                }
            }
            int res = sum();
            cout << res << endl;
        }

    }
    return 0;
}