POJ 1691 Painting a Board(状态压缩DP)
Description
The CE digital company has built an Automatic Painting Machine (APM) to paint a flat board fully covered by adjacent non-overlapping rectangles of different sizes each with a predefined color.
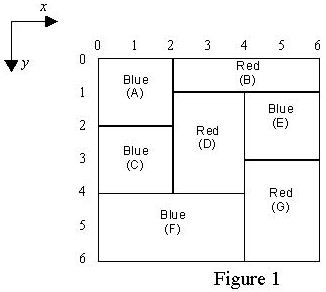
To color the board, the APM has access to a set of brushes. Each brush has a distinct color C. The APM picks one brush with color C and paints all possible rectangles having predefined color C with the following restrictions:
To avoid leaking the paints and mixing colors, a rectangle can only be painted if all rectangles immediately above it have already been painted. For example rectangle labeled F in Figure 1 is painted only after rectangles C and D are painted. Note that each rectangle must be painted at once, i.e. partial painting of one rectangle is not allowed.
You are to write a program for APM to paint a given board so that the number of brush pick-ups is minimum. Notice that if one brush is picked up more than once, all pick-ups are counted.

To color the board, the APM has access to a set of brushes. Each brush has a distinct color C. The APM picks one brush with color C and paints all possible rectangles having predefined color C with the following restrictions:
To avoid leaking the paints and mixing colors, a rectangle can only be painted if all rectangles immediately above it have already been painted. For example rectangle labeled F in Figure 1 is painted only after rectangles C and D are painted. Note that each rectangle must be painted at once, i.e. partial painting of one rectangle is not allowed.
You are to write a program for APM to paint a given board so that the number of brush pick-ups is minimum. Notice that if one brush is picked up more than once, all pick-ups are counted.
Input
The first line of the input file contains an integer M which is the number of test cases to solve (1 <= M <= 10). For each test case, the first line contains an integer N, the number of rectangles, followed by N lines describing the rectangles. Each rectangle R is specified by 5 integers in one line: the y and x coordinates of the upper left corner of R, the y and x coordinates of the lower right corner of R, followed by the color-code of R.
Note that:
Note that:
- Color-code is an integer in the range of 1 .. 20.
- Upper left corner of the board coordinates is always (0,0).
- Coordinates are in the range of 0 .. 99.
- N is in the range of 1..15.
Output
One line for each test case showing the minimum number of brush pick-ups.
Sample Input
1 7 0 0 2 2 1 0 2 1 6 2 2 0 4 2 1 1 2 4 4 2 1 4 3 6 1 4 0 6 4 1 3 4 6 6 2
Sample Output
3
思路:
1. 拓扑排序加深搜
2. 拓扑排序加广搜
3. 状态压缩DP. 设 dp[s][i] 表示当前状态为 s 时, 刚画完第 i 个矩形所用的最少画笔数. s = [1, 1<<15), s 的二进制表示中, 第 i 位 为1 表示第 i 个矩形已经被涂完色.
dp[news][i] = min(dp[news][i], dp[olds][j]+1) if color[i] != color[j]
= min(dp[olds][j]) if color[i] == color[j]
其中, news = (olds | 1<<i)
上述状态转移方程的意思是, 要计算 dp[s][i] 的值, 那么考虑当前所有 dp[olds][j], 其中 s = (olds|1<<i), 假如 j 的颜色和 i 的颜色相同, 这不需要另拿画笔, 否则, 画笔数加 1
当然, 对 i 进行涂色需要满足 i 的直接前驱都已被涂完
总结:
1. 这道题近似于暴力破解, 枚举所有状态集合的所有状态, 在某个状态 s 下, 以 s 中以涂色的某个矩形为支点来更新一个还未被涂色的点
2. 第 48 行代码错过一次, 把 i 写成了 j
3. 第 45 行很精髓, 我本打算用一个 for 循环进行判断的
4. 第 44, 48 行, 体现了 (1) 的思想, 即以 k 为支点来更新 i
代码:
#include <iostream>
using namespace std;
class tangle {
public:
int x1, y1, x2, y2;
int color;
tangle(int _x1, int _y1, int _x2, int _y2):x1(_x1), y1(_y1), x2(_x2), y2(_y2) {}
tangle() {
tangle(0, 0, 0, 0);
}
};
const int INF = 0X3F3F3F3F;
int M, N;
tangle tangles[20];
int dp[1<<15][20];
int up[20];
bool isUpper(int i, int j) {
if(tangles[i].x2 != tangles[j].x1) return false;
if(tangles[i].y1 >= tangles[j].y2) return false;
if(tangles[i].y2 <= tangles[j].y1) return false;
return true;
}
void pre_process() {
memset(up, 0, sizeof(up));
for(int i = 1; i <= N; i ++) {
for(int j = 1; j <= N; j ++) {
if(isUpper(i, j))
up[j] = (up[j]|(1<<(i-1)));
}
}
memset(dp, 0x3f, sizeof(dp));
for(int i = 1; i <= N; i ++)
if(up[i] == 0)
dp[1<<(i-1)][i] = 1;
}
int mainFunc() {
int END = (1<<N) -1;
for(int s = 1; s <= END; s ++) { // 从状态 s 导出 dp[s][i], 当前 s 第 i 个矩形不能被涂色
for(int i = 1; i <= N; i ++) { // 将要给第 i 个矩形涂色
if(s&(1<<(i-1)) ) continue; // 状态 s 中, 对应第 i 个矩形已经被涂完了
if((s&up[i]) != up[i]) continue; // 确保 i 的直接前驱都已涂完颜色
for(int k = 1; k <= N; k ++) {
if(!(s&(1<<(k-1)))) continue;
int news = (s|1<<(i-1)); // update 新的 dp[][]
if(tangles[i].color != tangles[k].color)
dp[news][i] = min(dp[news][i], dp[s][k]+1);
else
dp[news][i] = min(dp[news][i], dp[s][k]);
}
}
}
int ans = INF;
for(int i = 1; i <= N; i ++) {
ans = min(ans, dp[END][i]);
}
return ans;
}
int main() {
freopen("E:\\Copy\\ACM\\poj\\1691\\in.txt", "r", stdin);
cin >> M;
while( M -- >= 1) {
cin >> N;
for(int i = 1; i <= N; i ++) {
scanf("%d%d%d%d%d", &tangles[i].x1, &tangles[i].y1, &tangles[i].x2, &tangles[i].y2, &tangles[i].color);
}
pre_process();
cout << mainFunc() << endl;
}
return 0;
}


